If velocity of a particle is given by v=3t2−6t+4. Find its displacement from t=0 to 3secs.
Video Solution
Text Solution
The correct Answer is:12m
(i) x2∫x1dx=3∫0(3t2−6t+4)dt
displacement=(t3−3t2+4t)30=27−27+12m=12m
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the displacement of a particle is given by s=2t3−5t2+4t−3, then its displacement when acceleration is 14 ft/sec2, is
A1 feetB2 feetC3 feetD4 feetDuring one dimensional motion on x-axis Velocity time graph for particle is given.
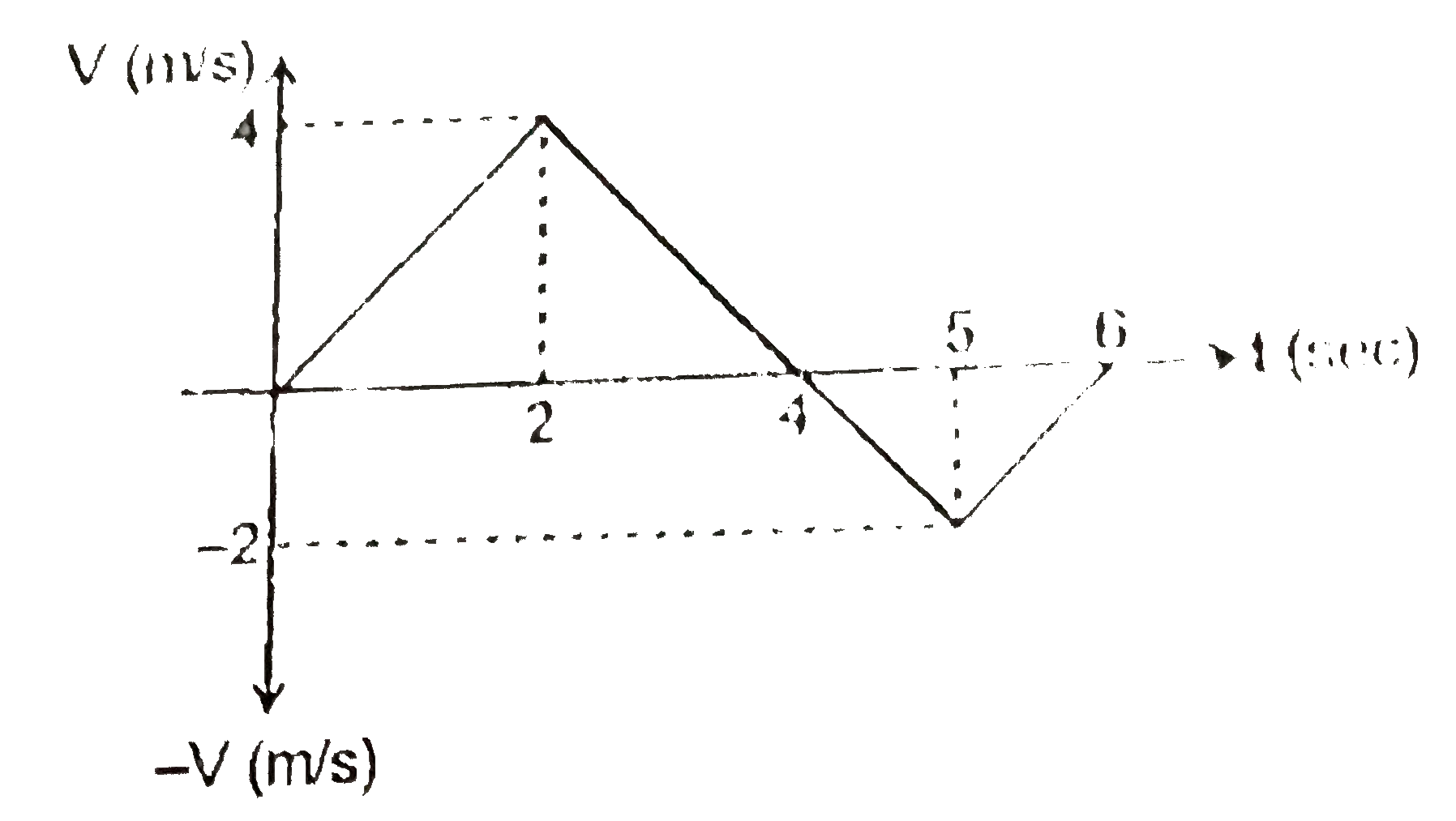
Find total displacement during (t = 0 sec) to (t = 6 sec)A6 mB10 mC8 mD2 mVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
A18ms−2B12ms−2C15ms−2Dzero
The displacement of a particle at time t is given by s=2t3−5t2+4t−3 . Find the velocity when t = 2 sec.
View SolutionThe velocity of a particle is given by v=u0+gt+12at2. If its position is x=0 at t=0, then what is its displacement after t=1s ?
View SolutionThe displacement s of a particle at a time t is given bys=t3−4t2−5t. Find its velocity and acceleration at t = 2.
View SolutionThe acceleration of a particle is given by, a = t/6 at t = 0, velocity v = 2 m/s, displacement s= 2m. Find the velocity at t= 4 seconds,
View SolutionIf the displacement of a particle is given by s=2t3−5t2+4t−3, then its acceleration is 14 ft/sec2 after to,e
View Solution

