Two ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them at time t is :-
a2y+bx2=0
a2y=bx2
y=ba2x
ay2=b2x
The correct Answer is:B
l=√(100−2t)2+(200−4t)2

Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 3
5 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 4
6 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 1
5 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Two ships, 1 and 2, move with constant velocities 3 m/s and 4 m/s along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0 the ships were located at the distances 120 m and 200 m from the point O. How soon will the distance between the ships become the shortest and what is it equal to ?
View SolutionTwo particles, 1 and 2, move with constant velocities v1 and v2 along two mutually perpendicular straight lines toward the intersection point O. At the moment t=0 the particles were located at the distances l1 and l2 from the point O. How soon will the distance between the particles become the smallest? What is it equal to?
View Solution
Knowledge Check
Two ships, V and W, move with constant velocities 2ms−1 and 4ms−1 along two mutually perpendicular straight tracks toward the intersection point O. At the moment t=0, the ships V & W were located at distances 100m and 200m respectively from the point O.
The distance between them will be shortest at t= ........A2bˆjBaˆjC(a−2b)ˆiDNone of theseTwo particles are moving along two long straight lines, in the same plane with same speed equal to 20cm/s. The angle between the two linse is 60∘ and their intersection point isO. At a certain moment, the two particles are located at distances 3m and 4m from O and are moving twowards O. Subsequently, the shortest distance between them will be
A50cmB40√2cmC50√2cmD50√3cmTwo particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is
 A50√3cmB300cmC100√3cmD200cm
A50√3cmB300cmC100√3cmD200cm
Two particles A and B move with constant velocities v1 and v2 along two mutually perpendicular strainght lines. Towards the intersection point O. At moment t=0 the particle were located at distance l1 and l2 from O respectively. Find the time when they are nearest and also this shortest distance
View SolutionTwo points A and B located in diametrically opposite directions of a point charge of +2μC at distances 2.0 m and 1.0 m respectively from it. Determine the potential difference VA−VB
View SolutionTwo boats, A and B, move away from a point P at the middle of a river along the mutually perpendicular straight lines. Boat A moves along the river and boat B across the river. Having moved off equal distance from point P the boats returned. find the ratio of times of motion of boats tAtB if v=ηu(η>1). (v : velocity of boat with respect to water. u: stream velocity)
View SolutionTwo ships A and B are sailing straight away from the foot of a tower OP along routes such that ∣AOB––––––– is always 120∘. At a certain instance, the angles of depression of the ships A and B from the top P of the towers are 60∘and30∘ respectively. The distance between the ships when the height of the tower is 15m is
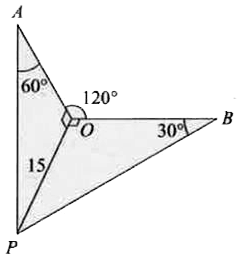
View SolutionRam Shyam are walking on two perpendicular tracks with speed 3ms−1and4ms−1, respectively. At a certain moment (say t = 0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
Shortest distance between them subsequently is
View Solution
