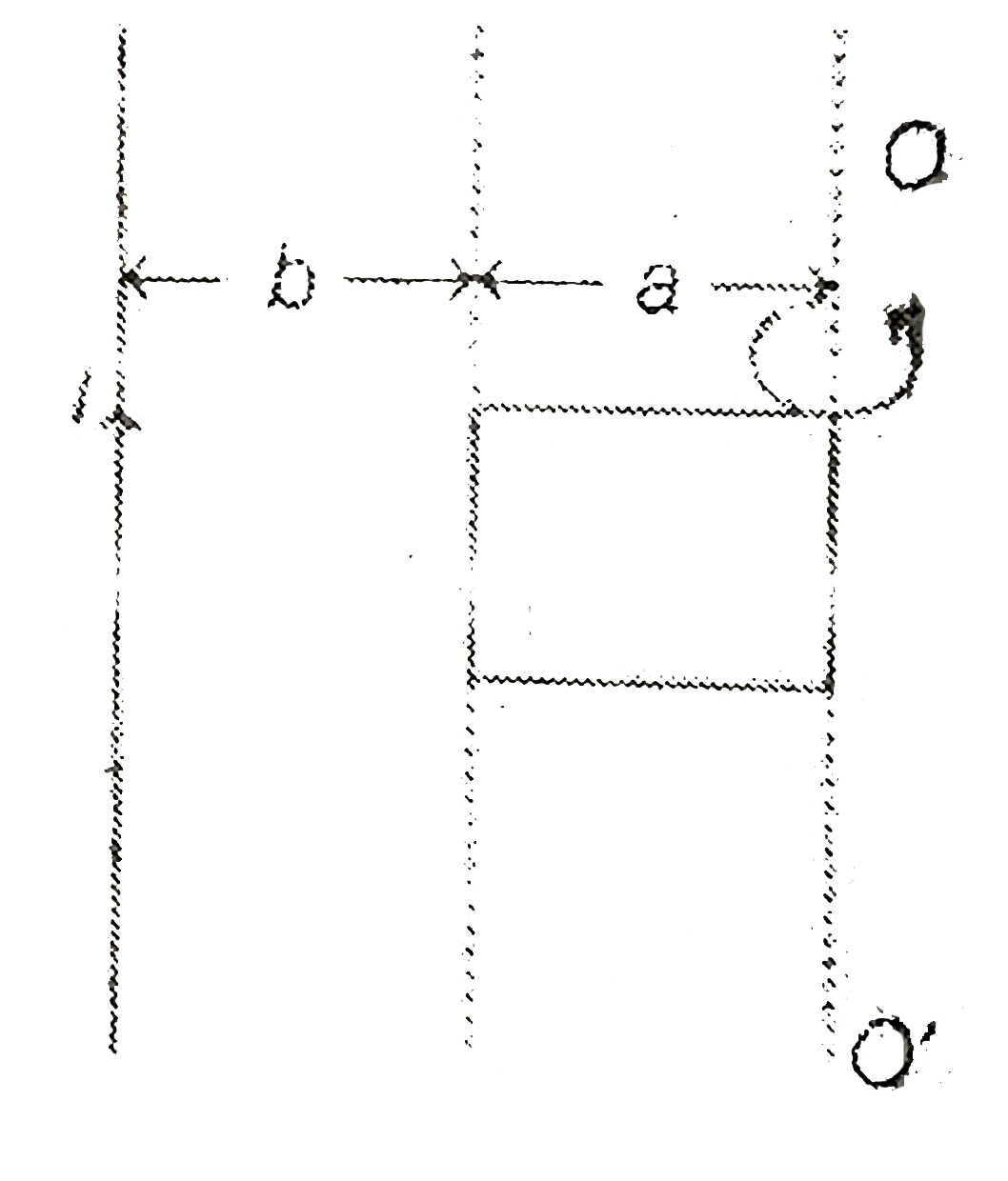
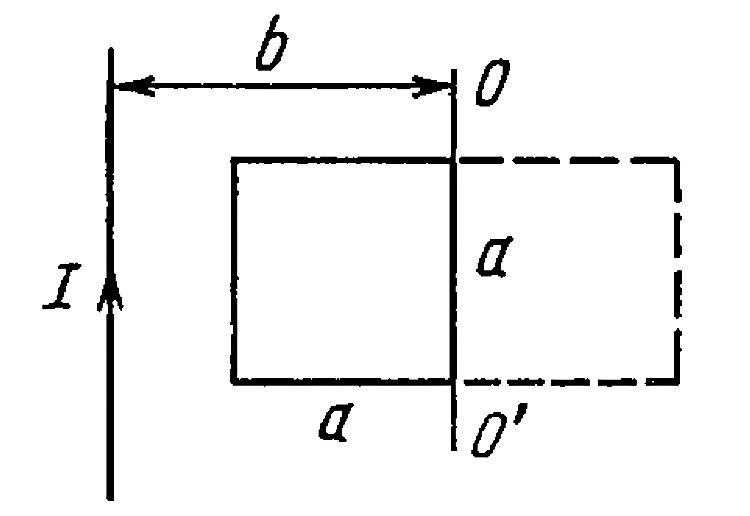
A square loop of side as and a straight long wire are placed in the same plane as shown in figure. The loop has a resistance R and inductance L. The frame is turned through 180∘ about the axis OO′. What is the electric charge that flows through the loop?

The correct Answer is:4
After moving the loop about side PQ through 120∘ the normal on the side PS from the wire will be passing through midpoint C and net magnetic, flux through the loop in the new position will be zero.
∴ Changes is flux △f= Flux through the loop in the initial position

dϕ=→B.d→Aμ0I2πxa.dx
ϕ=∫2aaμ0Iadx2πx=μ0Ia2πln(2)
∴ charge flown through the square loop =△ϕR=μ0Ia2πRIn(2)
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
A square loop of side and a straight infinity conducor are placed in the same plane with two sides of the squre parallel to the conductor. The resistance of the loop is R. The loop is turned through 180∘ about the axis . The electric charge that flows in the square loop is μ0Ia2πR1m∣∣∣na+bb∣∣∣. Find the value of n.
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View Solution
Knowledge Check
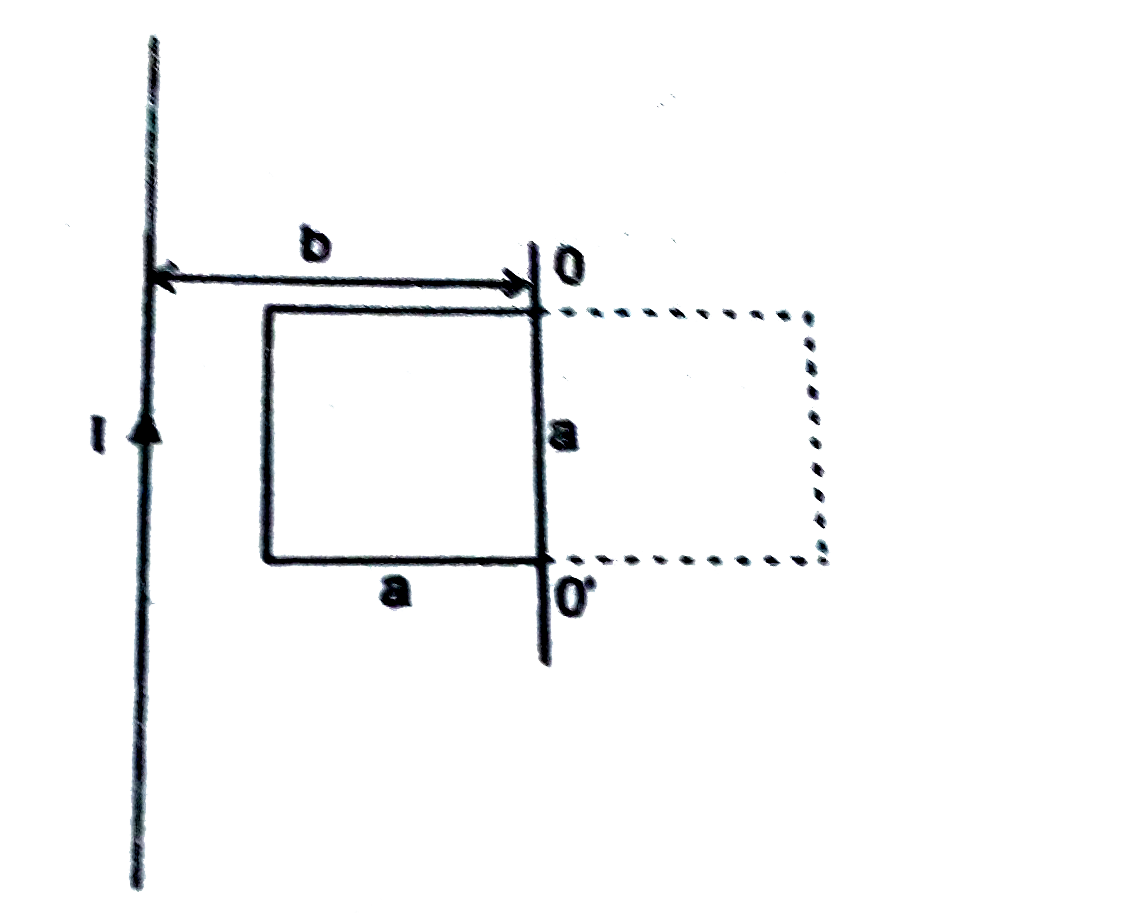
A square frame with side 'a' and a straight conductor carrying a constant current I are located in the same plane. The resistance of the frame is equal to R. The frame was turned through 180∘ about the axis OO' separated from the current-carrying conductor by a distance b=2a. If the electric charge that flowed through the frame be expressed as a function of a,I,R it takes the form q=constant ×am×In×Rp. Find m+n+p.
A1B2C3D4A current I flows through a closed loop as shown in figure. The magnetic field induction at the centre 0 is
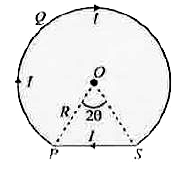 Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
Aμ0I4πRθBμ0I4πR(θ+sinθ)Cμ0I4πR(π−θ+sinθ)Dμ0I4πR(π−θ+tanθ)
A square wire frame ( initially current is zero) with side a and a straight conductor carrying a constant current I are located in the same plane (figure). The inductance and the resistance of the frame are equal to L and R respectively. The frame was turned through 180∘ about the axis OO' separated from the current - carrying conductor by a distance b=2a. The total electric charge having flown through the frame if i=0 at t=0 in the loop is equal to μ0aI2πRlnx. Find the value of x.
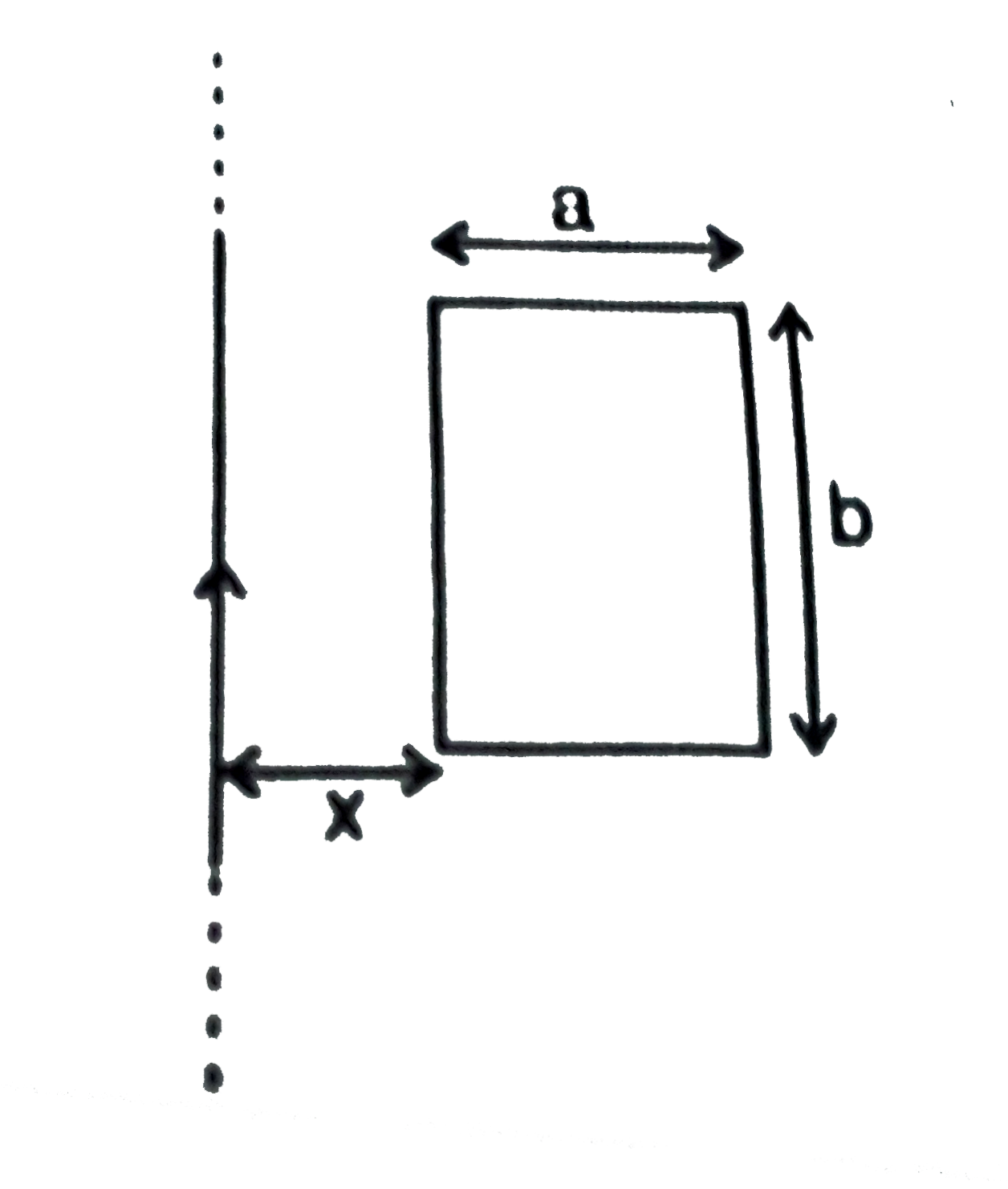
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.
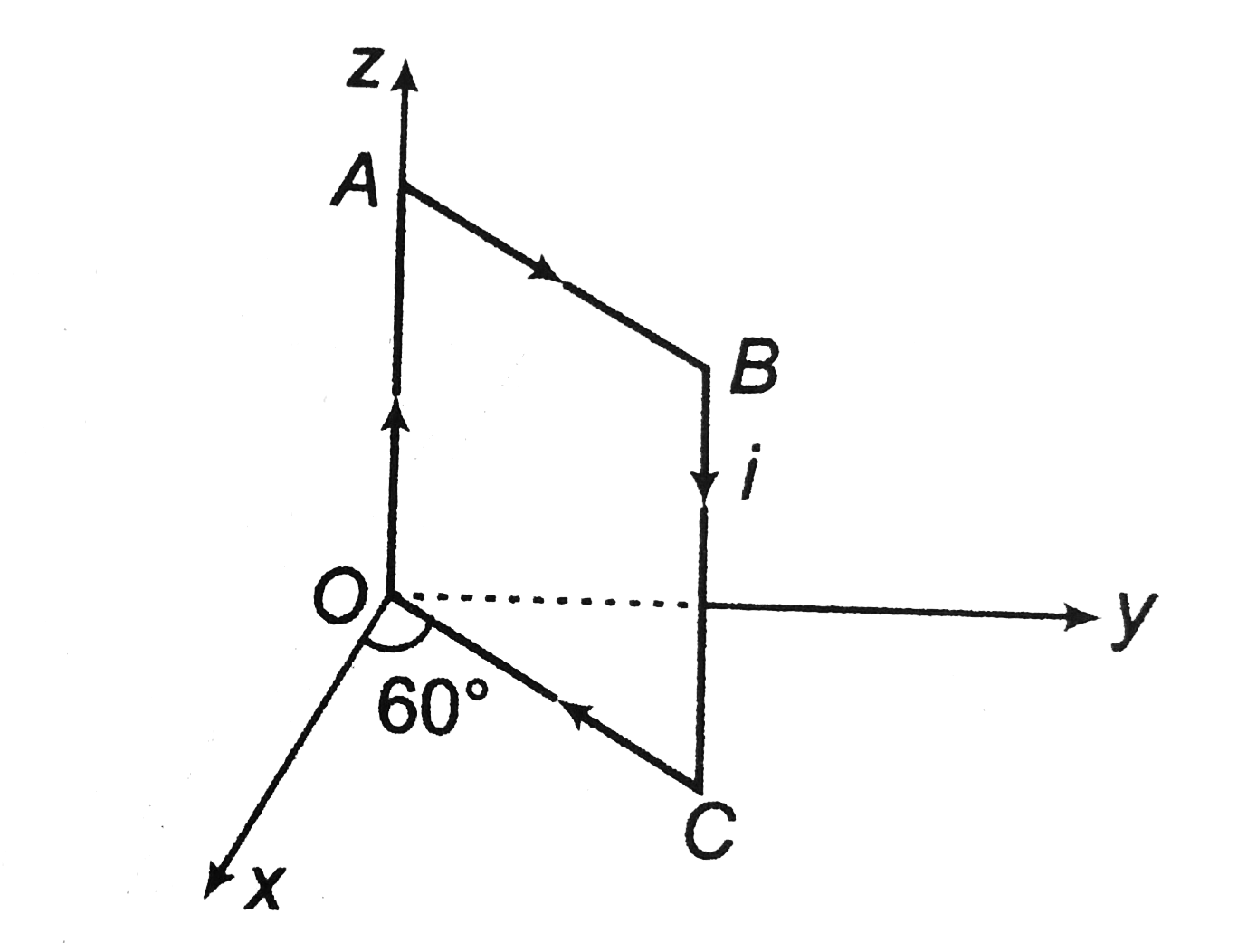
View SolutionA square loop is placed near a long current carrying straight wire as shown in the figure . Match the following table


View SolutionA square wire frame with side a and a straight conductor carrying constant current I are located in the same plane (Fig). The inductance and the resitance of the frame are equal to L and R respectively. The frame was turned throgh 180∘ about the axis OO'separated fromt the current carrying conductor by a distance b. FInd the electric charge having flown through the frame.
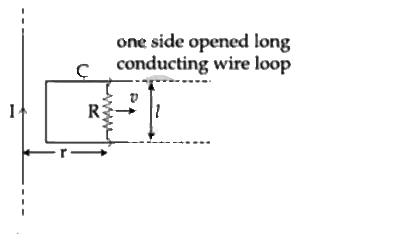
View SolutionAn infinitely long straight wire carrying current I , one side opened rectangular loop and a conductor C with a sliding connector are located in the same plane , as shown in the figure. The connector has length l and resistance R . It slides of the right with a velocity v. The resistance of the conductor and the self inductance of the loop are negligible . The induced current in the loop , as function of separation r between the conductor and the straight wire is :
View Solution
