What values for x would make 1√x+1 undefined ?
−1 only
1 only
All real numbers greater than -1
All real numbers less than or equal to -1
The correct Answer is:D
To determine the values for x that would make the expression 1√x+1 undefined, we need to analyze the conditions under which the denominator becomes zero or the expression inside the square root becomes negative.
1. Identify the Denominator: The expression is 1√x+1. The denominator is √x+1.
2. Condition for Undefined Expression: The expression is undefined when the denominator is zero. Therefore, we need to find when:
√x+1=0
3. Solve for x: To find when the square root is zero, we set:
x+1=0
Solving for x gives:
x=−1
4. Condition for Square Root: Additionally, the square root is only defined for non-negative values. Thus, we need:
x+1≥0
This simplifies to:
x≥−1
5. Combine Conditions: The expression 1√x+1 is undefined for:
- x=−1 (where the denominator becomes zero)
- x<−1 (where the expression under the square root becomes negative)
6. Conclusion: Therefore, the expression is undefined for all values of x that are less than or equal to -1.
Final Answer:
The values for x that would make 1√x+1 undefined are:
x≤−1
√x+1=0
x+1=0
Solving for x gives:
x=−1
x+1≥0
This simplifies to:
x≥−1
- x=−1 (where the denominator becomes zero)
- x<−1 (where the expression under the square root becomes negative)
The values for x that would make 1√x+1 undefined are:
x≤−1
Topper's Solved these Questions
Similar Questions
Knowledge Check
For which nonnegative value of b is the expression 12−b2 undefined?
A0B√2C2D8If f(x)=1√1−x2, which of the following describes all the real values of x for which f(x) is undefined ?
Ax=−1 or x = 1Bx<−1 or x>1Cx≤−1 or x≥1D−1<x<1For which values of x in the expression 3x+63x(4x+8)(x−5) undefined?
A−2B−2,5C0,−2,5D0,2,−5
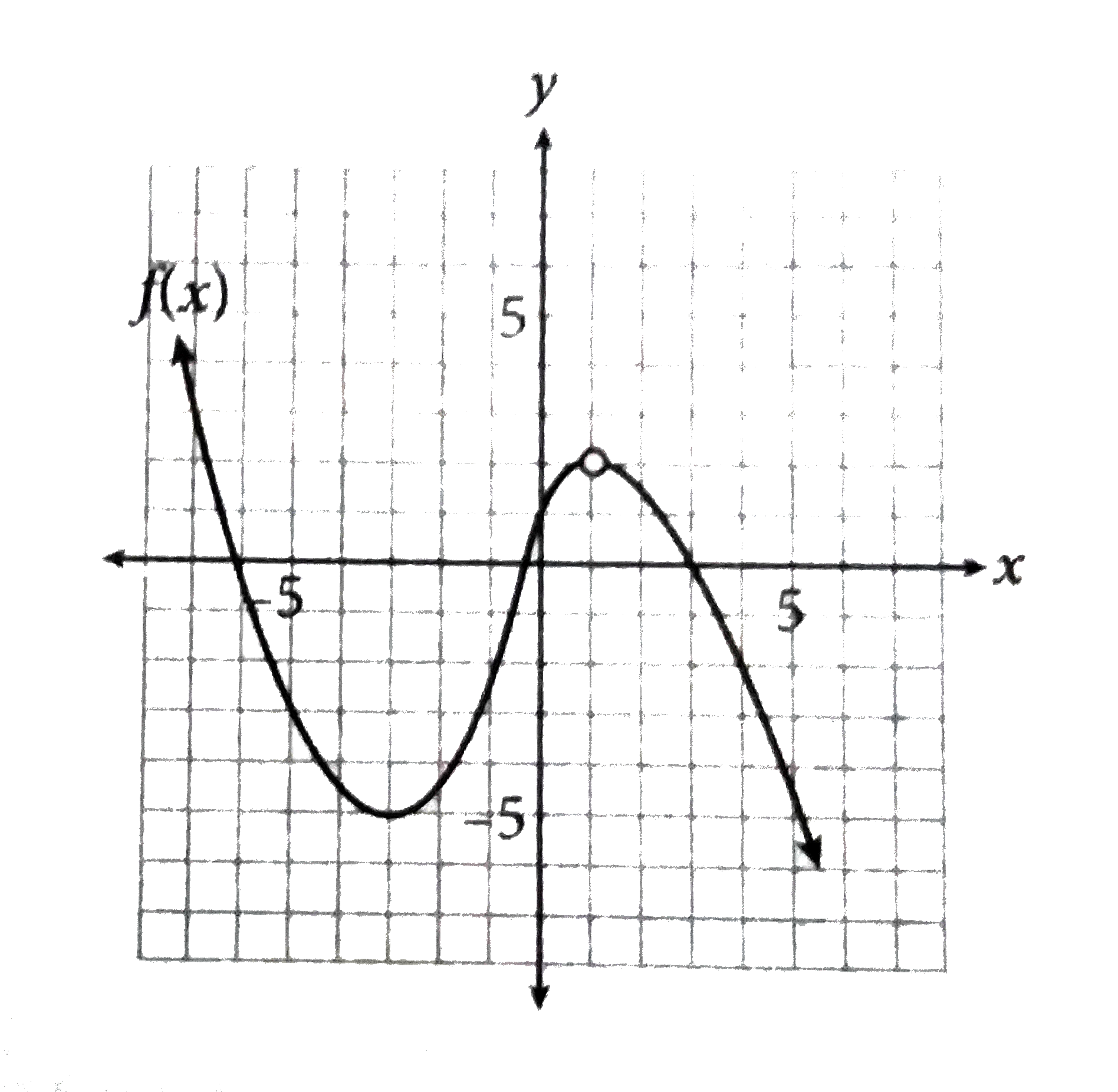
The graph of y=f(x) is given above. For what value of x is y=f(x-4) undefined?
View SolutionThe set of values of x for which
tan−1(x)√1−x2=sin−1 x holds is
View SolutionThe value of n∑r=11√a+rx+√a+(r−1)x is -
View SolutionThe values of x for which 11+√x,11−x,11−√x are in A.P. lie in the interval (A) (0,∞) (B) (1,∞) (C) (0,1) (D) none of these
View SolutionWhich of the following is a value of x for which the expression −3x2+3x−10 is undefined ?
View Solution

