If point P is located on the unit circle, then x+y=

0.37
0.50
0.78
1.37
The correct Answer is:D
Draw in a right triangle :
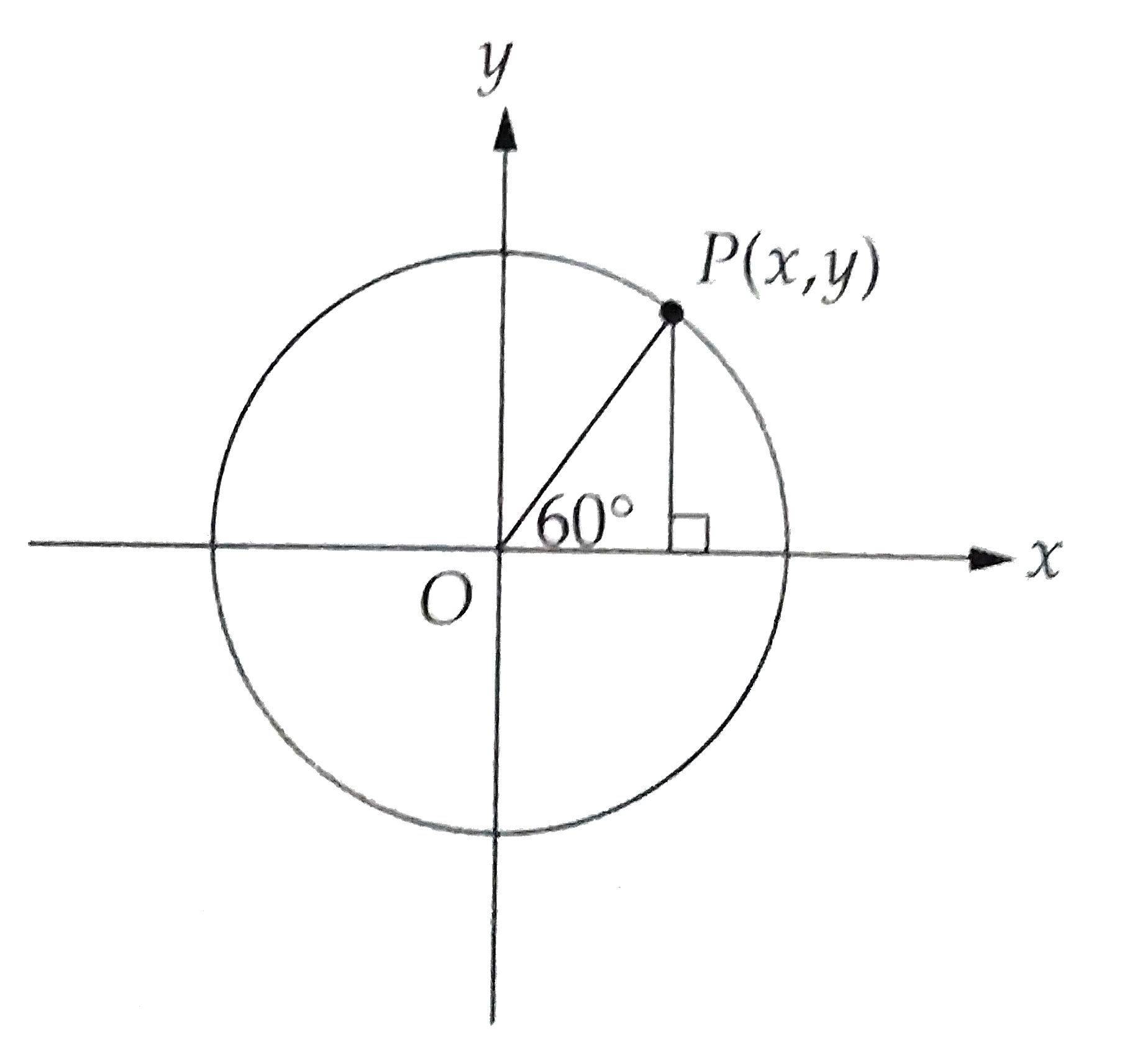
That's a 30-60-90 triangle. The hypotenuse is the radius, so it's 1. That means that the short leg is 12 and the long leg is √32 :
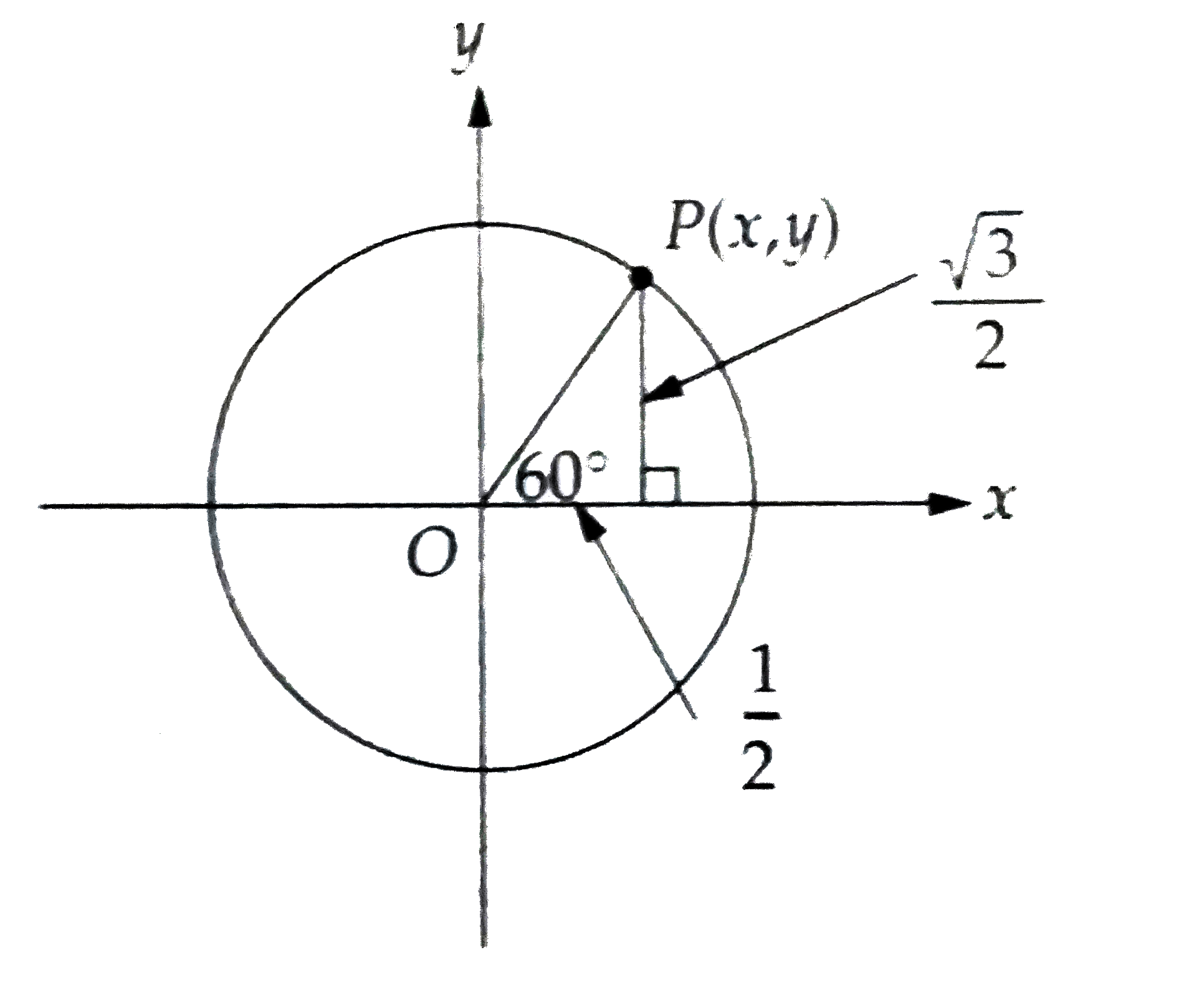
so, x+y=12+√32≈1.37.
Topper's Solved these Questions
Similar Questions
Point P is on the unit circle with center at O and point A is the point at which the unit circle intersects the positive x-axis. If angle AOP measures 7π6 radians, what are the coordinates of point P?
View SolutionA point "P" is at the 9 unit distance from the centre of a circle of radius 15 units. The total number of different chords of the circle passing through point P and have integral length is
View Solution
Knowledge Check
A circle in the xy-plane is defined by the equation (x−4)2+(y+2)2=100. Which of the following points is located on the circumference of the circle ?
A(−3,5)B(0,9)C(4,−2)D(4,8)
Locate the position of the point P with
resect to the circle S=0 when
P(4,2)andS≡2x2+2y2−5x−4y−3=0
View SolutionIf point P(x,y) is called a lattice point if x,y∈I. Then the total number of lattice points in the interior of the circle x2+y2=a2,a≠0 can not be:
View SolutionIf a chord of contact of tangents drawn from a point P with respect to the circle x2+y2=9 is x=2, then area, in square units, of triangle formed by tangents drawn from P to the circle and their chord of contact is equal to
View SolutionA particle from the point P(√3,1) moves on the circle x2+y2=4 and after covering a quarter of the circle leaves it tangentially. The equation of a line along with the point moves after leaving the circle is
View SolutionA chord of the circle x2+y2=a2 cuts it at two points A and B such that ∠AOB=π/2, where O is the centre of the circle. If there is a moving point P on this circle, then the locus of the orthocentre of ΔPAB will be a
View SolutionLocate the position of the point P with respect to the circle S=0 when
(i) P(1,2) and S=x2+y2+6x+8y−96
(ii) P(3,4) and S=x2+y2−4x−6y−12
(iii) P(2,-1) and S=x2+y2−2x−4y+3
(iv) P(1,5) and S=x2+y2−2x−4y+3
View SolutionThe number of points P(x,y) lying inside or on the circle x2+y2=9 and satisfying the equation tan4x+cot4x+2=4sin2y is______
View Solution

