In the figure above, the bases of the right uniform solid are triangles with sides of length 5, 12, and 13. If the surface area of the solid is 360, what is the volume ?

A
30
B
180
C
300
D
600
Video Solution
Text Solution
The correct Answer is:C
The surface area is the sum of the areas of the faces. To find the areas of the faces, you need to figure out what kinds of polygons they are so that you'll know what formulas to use. Start with the bases, which are said to be ''triangles with sides of lengths 5, 12, and 13.'' If these side lengths don't ring a bell in your head, go back and study your Pythogorean triplets. This is a 5-12-13 triangle, which means it's a right triangle, which means that you can use the legs as the base and height to find the area :
Area of Right Triangle =12(leg1)(leg2)=12(5)(12)=30
That's the area of each of the bases. Now call the height of the solid h. The other three faces are rectangles with areas 5×h,12×h, and 13×h. The total surface area, then, is 30+30+5h+12h+13h=60+30h.
Since the problem tells us that the surface area is 360,
60+30h=360
h=10
Volume = base × height =30×10=300. The answer is (C ).
|
Topper's Solved these Questions
- SOLID GEOMETRY Book:KAPLANChapter:SOLID GEOMETRY Exercise:SOLID GEOMETRY FOLLOW - UP TEST
Explore 5 Videos
- SIMILARITY, CONGRUENCE, AND PROOFSBook:KAPLANChapter:SIMILARITY, CONGRUENCE, AND PROOFSExercise:Multiple Choice Question
Explore 10 Videos
- SYSTEM OF LINEAR EQUATION Book:KAPLANChapter:SYSTEM OF LINEAR EQUATION Exercise:Multiple Choice Question
Explore 20 Videos
Similar Questions
Knowledge Check
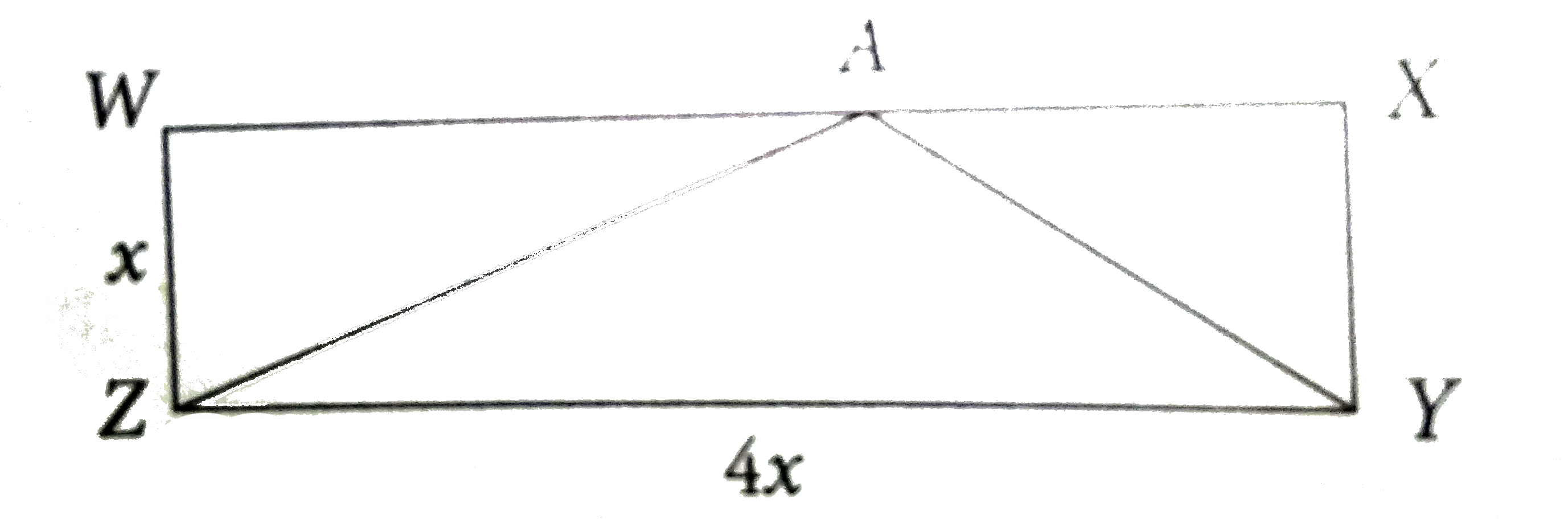
In the figure above, what is the area of triangle YAZ?A3xB5xC2x2D4x2Find the area of an equilateral triangle with a side length of 12
A6√3B18√3C36√3D72√3In the figure above, the bases , ABC and DEF, of the right prism are equilateral triangles. The altitude of the prism is BE. If a plane cuts the figure through points A, C and E, two solids, EABC, and EACFD, are formed. What is the ratio of the volume of EABC to the volume of EACFD?
A14B13C√34D12
The area of the base of a conical solid is 38.5cm2 and its volume is 154cm3. Find the curved surface area of the solid.
View SolutionThe area of the triangle whose sides. are 5 cm, 13 cm and 12 cm is
View SolutionThe sum of the radius of the base and height of a solid cylinder is 37m. If the total surface area of the solid cylinder is 1628 cm2. Find the volume of the cylinder.
View SolutionThe sum of the radius of the base and height of a solid cylinder is 37m. If the total surface area of the solid cylinder is 1628 cm2. Find the volume of the cylinder.
View SolutionTwo sides of a triangle have lengths of 5 and 19. Can the third side have a length of 13?
View Solution