Question

The pyramid in Figure composed of a square base of area 16 and four isoceles triangles, in which each base angle measures ${60}^{\circ }$. What is the volume of the pyramid ?

Options

A. `7.39`
B. `9.24`
C. `15.08`
D. `21.33`

Answer

C

Explanation

The sides of the pyramid are actually equilateral (the base angles are each `60^(@)`, which means the last angle is also `60^(@)`). To find the volume of a pyramid, you need the area of the base, which is given here as 16, and you need the height, which you have to figure out. Imagine a triangle that includes the height and one of the lateral edges :

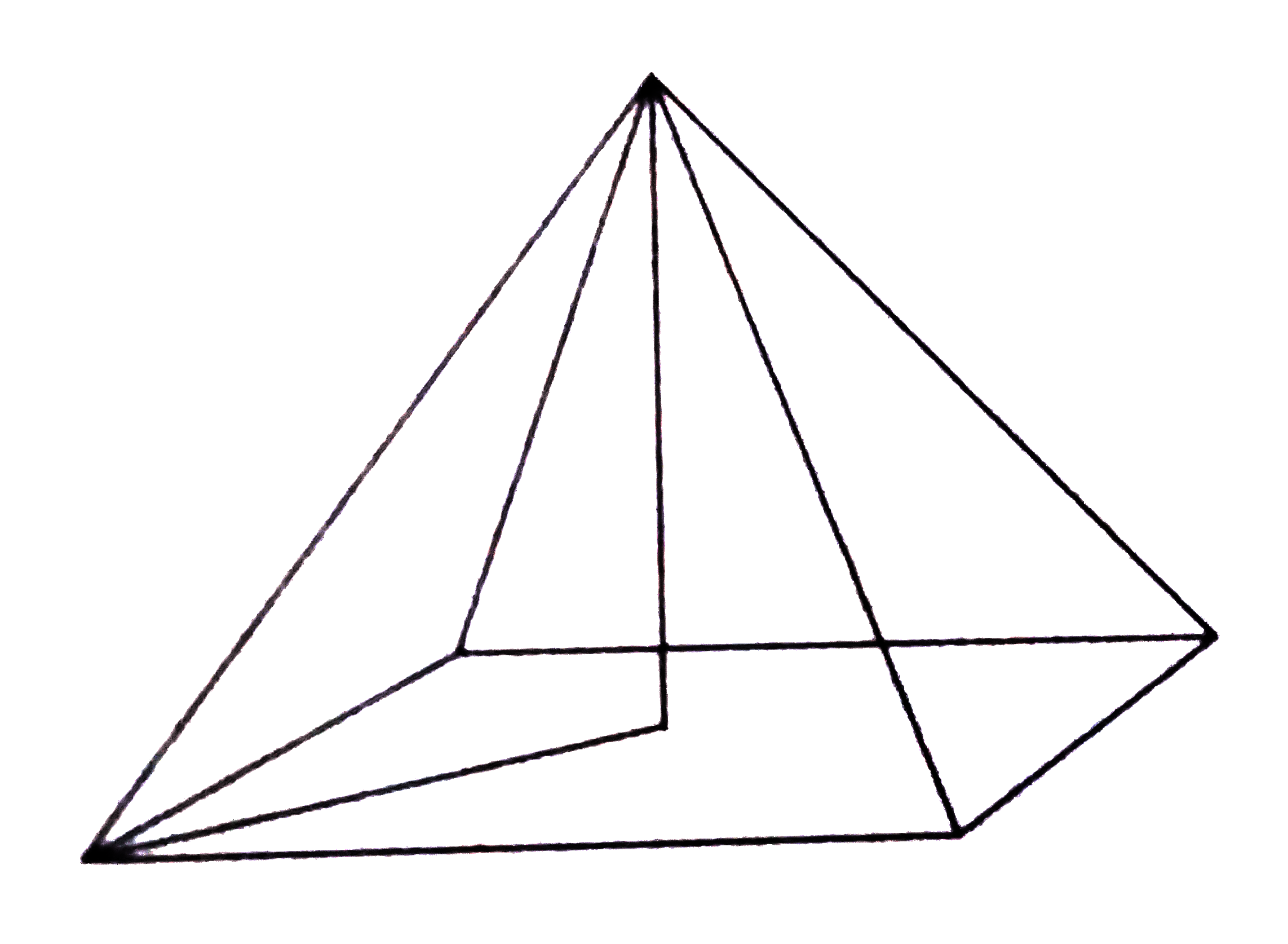
This triangle is a right triangle. The hypotenuse is the same as a side of one of the equilateral triangles, which is the same as a side of the square, which is the square root of 16, or 4 :

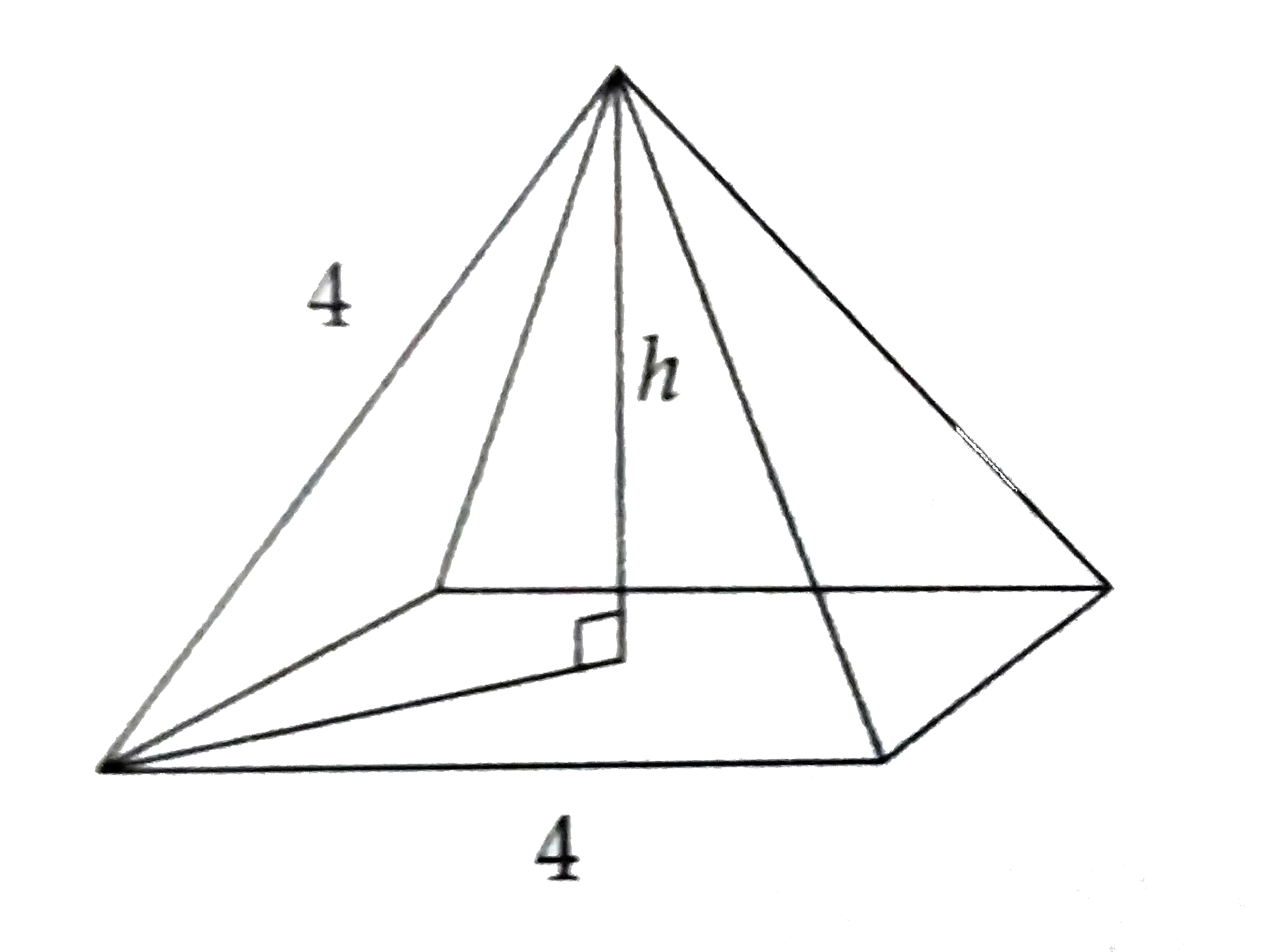
One of the legs of this triangle is half of a diagonal of the square base - that is, half of `4sqrt(2)`, or `2sqrt(2)`.

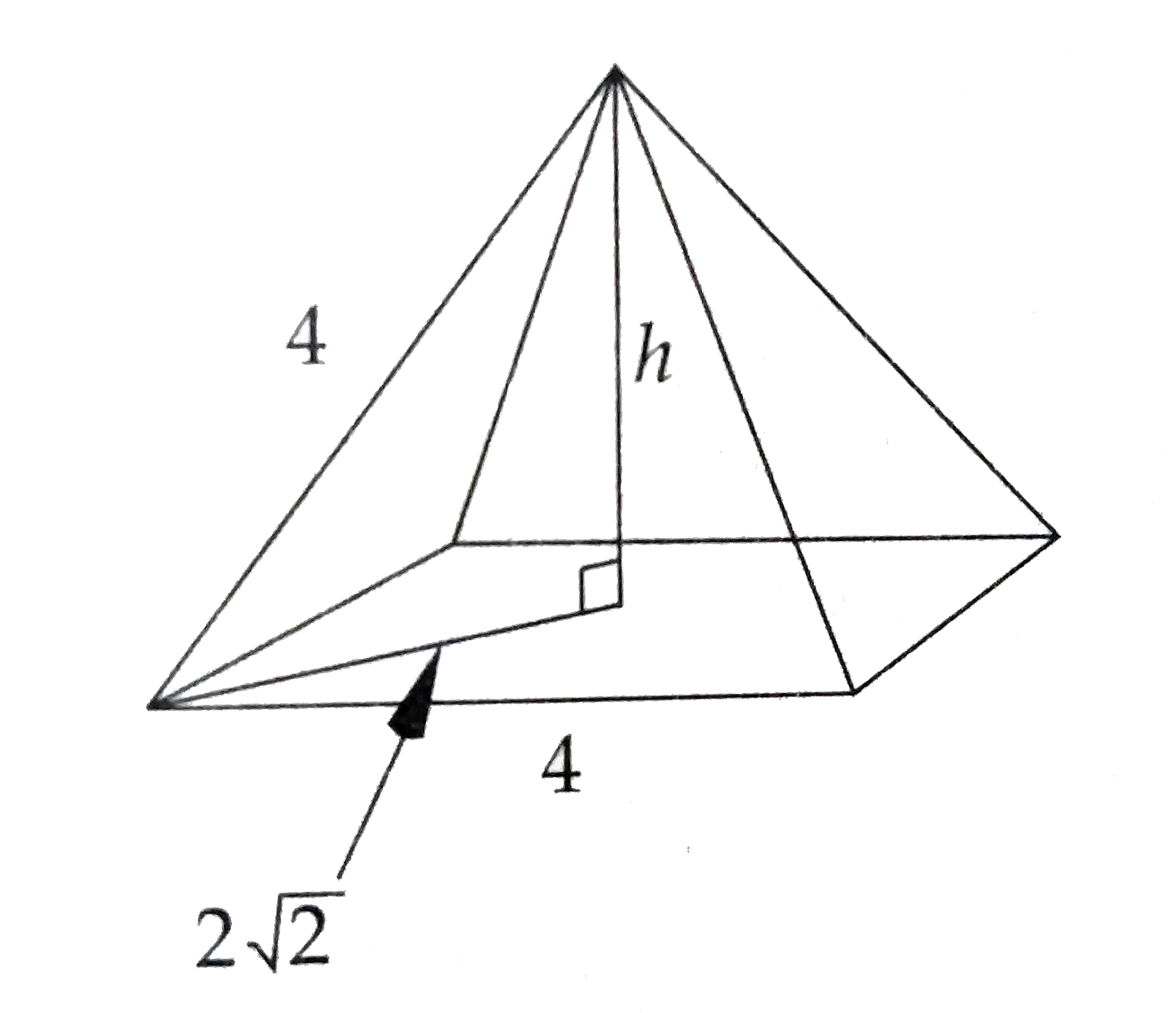
Now you can use the Pythagorean theorem to find the height :
`(2sqrt(2))^(2)+h^(2)=16`
`8+h^(2)=16`
`h^(2)=8`
`h=sqrt(8)=2sqrt(2)`
Finally, you have what you need to use the volume formula :
Volume `=(1)/(3)Bh=(1)/(3)(16)(2sqrt(2))=(32sqrt(2))/(3)~~15.08`