In the reactangular solid in Figure, what is the distance from vertex R to vertex T ?

2√19
2√17
8√2
10√2
The correct Answer is:A
One way to find this distance is to apply the Pythagorean theorem twice. First plug the dimensions of the base into the Pythagorean theorem to find the diagonal of the base :
Diagonal of base =√(3√2)2+(5√2)2=√18+50=√68=2√17
Notice that the base diagonal with an edge and with the segment ¯¯¯¯¯¯RT - the segment you're looking for - to form a right triangle :
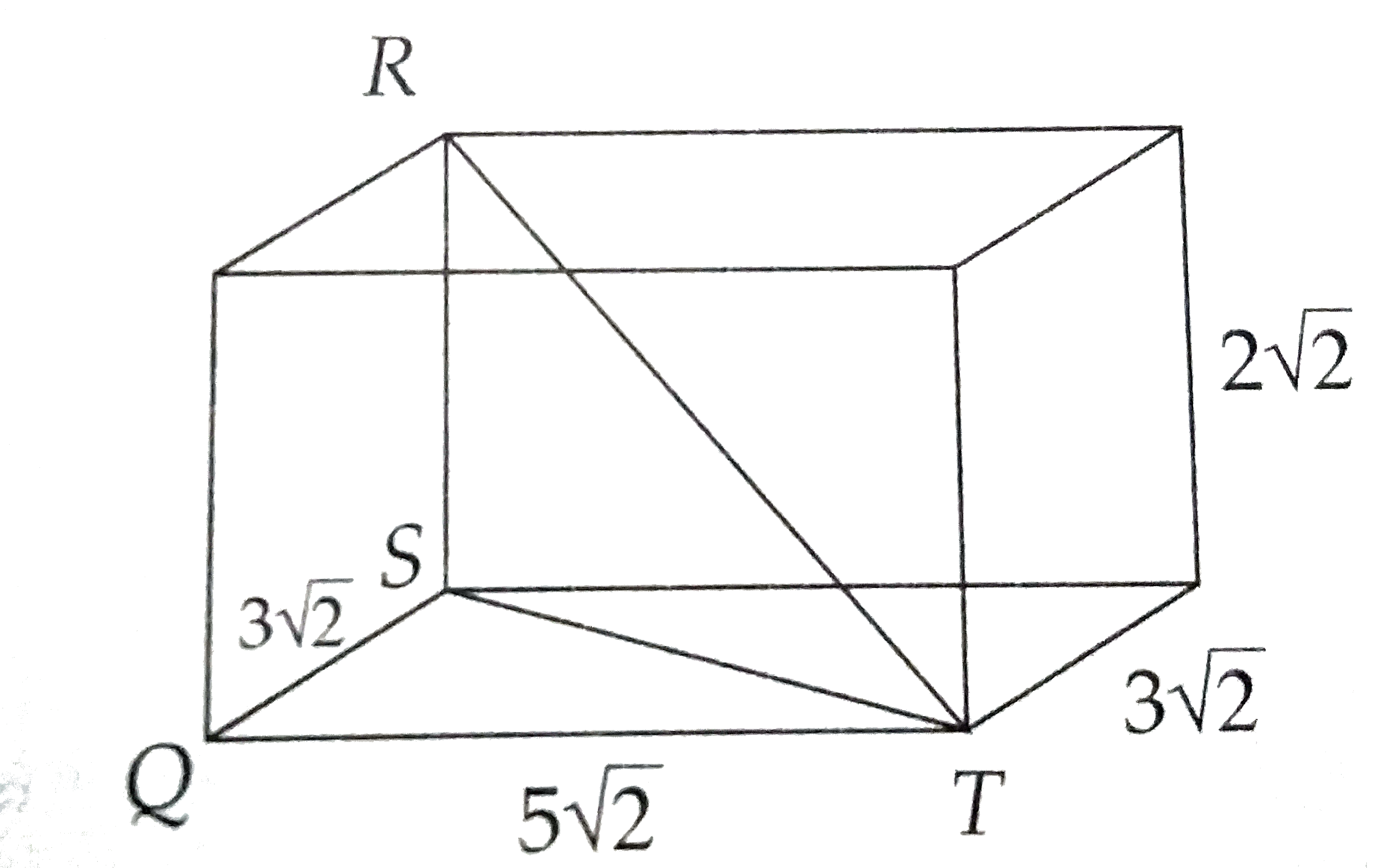
So you can plug the base diagonal and the height into the Pythagorean theorem to find ¯¯¯¯¯¯RT :
¯¯¯¯¯¯RT=√(2√22+(2√17)2)=√8+68=√76=2√19
The answer is (A).
Topper's Solved these Questions
- SOLID GEOMETRY BOOK - KAPLANCHAPTER - SOLID GEOMETRY EXERCISE - SOLID GEOMETRY FOLLOW - UP TEST
5 Videos
- SIMILARITY, CONGRUENCE, AND PROOFSBOOK - KAPLANCHAPTER - SIMILARITY, CONGRUENCE, AND PROOFSEXERCISE - Multiple Choice Question
10 Videos
- SYSTEM OF LINEAR EQUATION BOOK - KAPLANCHAPTER - SYSTEM OF LINEAR EQUATION EXERCISE - Multiple Choice Question
20 Videos
Similar Questions
The slope of a median, drawn from the vertex A of the triangle ABC is -2. The co-ordinates of vertices B and C are respectively (-1, 3) and (3, 5). If the area of the triangle be 5 square units, then possible distance of vertex A from the origin is/are.
View SolutionThe four lines drawing from the vertices of any tetrahedron to the centroid to the centroid of the opposite faces meet in a point whose distance from each vertex is 'k' times the distance from each vertex to the opposite face, where k is
View Solution
Knowledge Check
The centre of gravity of a hollow cone of height h is at distance x from its vertex where the value of x is:
Ah/3Bh/4C2h/3D3h/4The equation of a parabola in the xy-plane is y=2x2−12x+7. What is the distance between the vertex of the parabola and the point (3,4)?
A6B8C11D15
Find the locus of a point which is such that, the three normals through it cut the axis in points whose distance from the vertex are in A.P.
View SolutionThe area cut off from a parabola by any double ordinate is k time the corresponding rectangle contained by the double ordinate and its distance from the vertex. Find the value of k ?
View SolutionThe focus of a parabolic mirror as shown in the figure alongside is at a distance of 6cm from its vertex. If the mirror is 20cm deep, find the distance BC.
View SolutionThe focus of a parabolic mirror as shown in figure is at a distance of 5 cm from its vertex. If the mirror is 45 cm deep, find the distance AB
View SolutionFind the area of a parallelogram given in the figure. Also, find the length of the altitude from vertex A on the side DC.
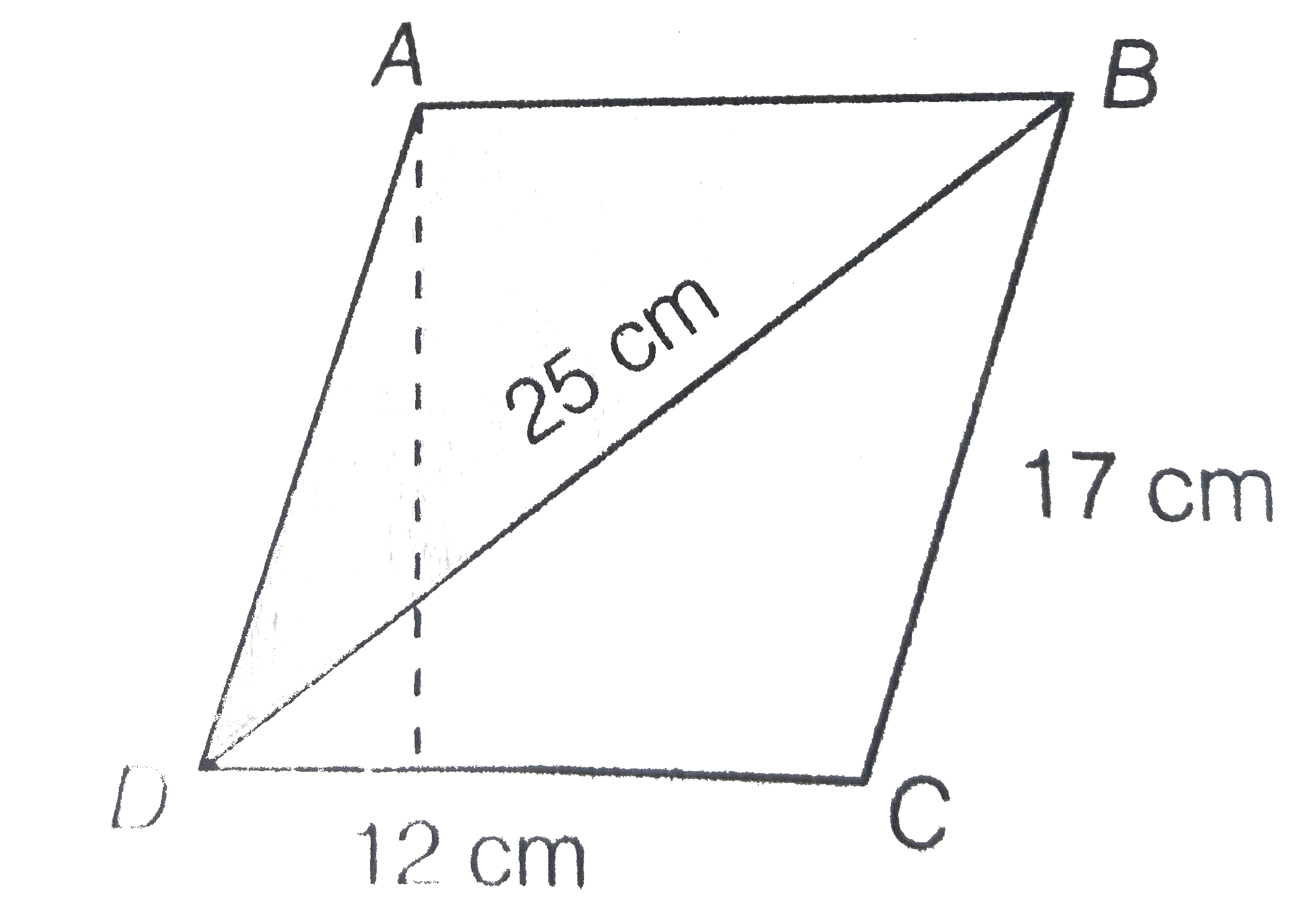
View SolutionProve that the length of a focal chord of a parabola varies inversely as the square of its distance from the vertex.
View Solution
