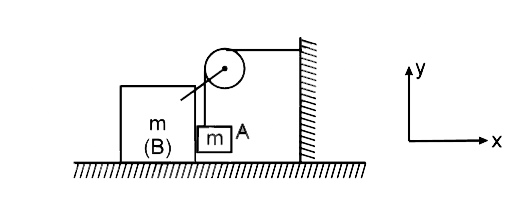
Two boxes A and B of masses m and M interconnected by an ideal rope and ideal pulleys are held at rest as shown. When it is released, box B accelerates downwards. Find velocities of box A and B as function of time t after system has been released.
We first explore relation between velocities vA and vB of the boxes A and B, which can be written either by using constrained relation or method of virtual work or by inspection.
vA=2vB ....(i)
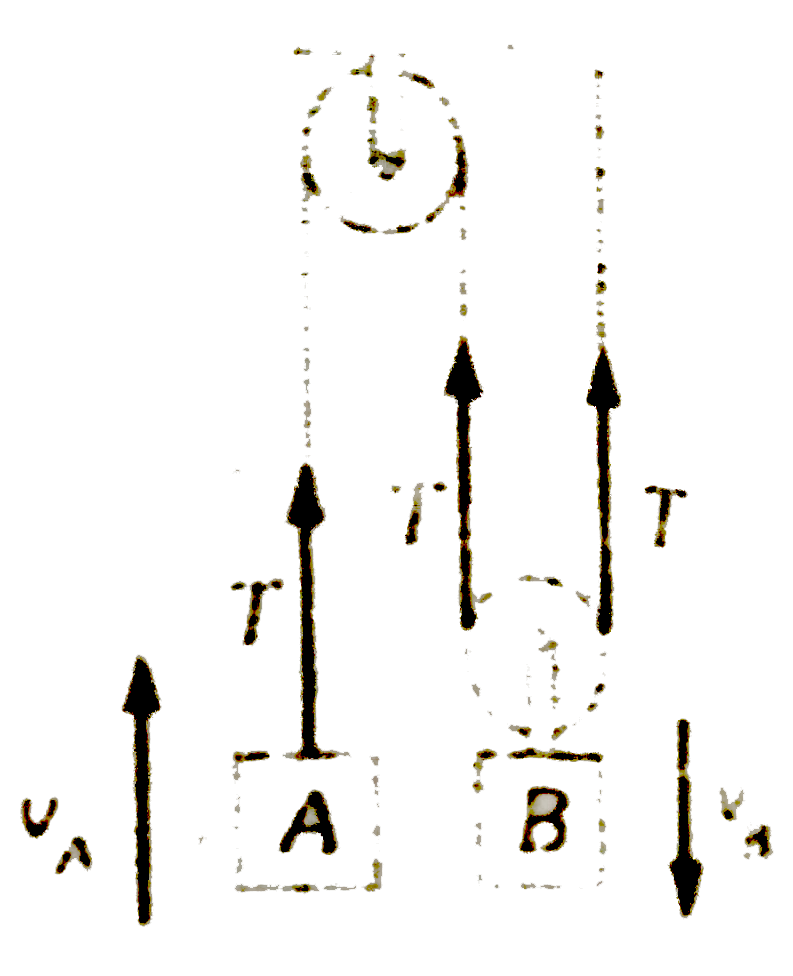
Applying impulse momentum principle to box A
P2y=P1y+∑Imp,y→ mvB=0+Mgt−2Tt ...(ii)
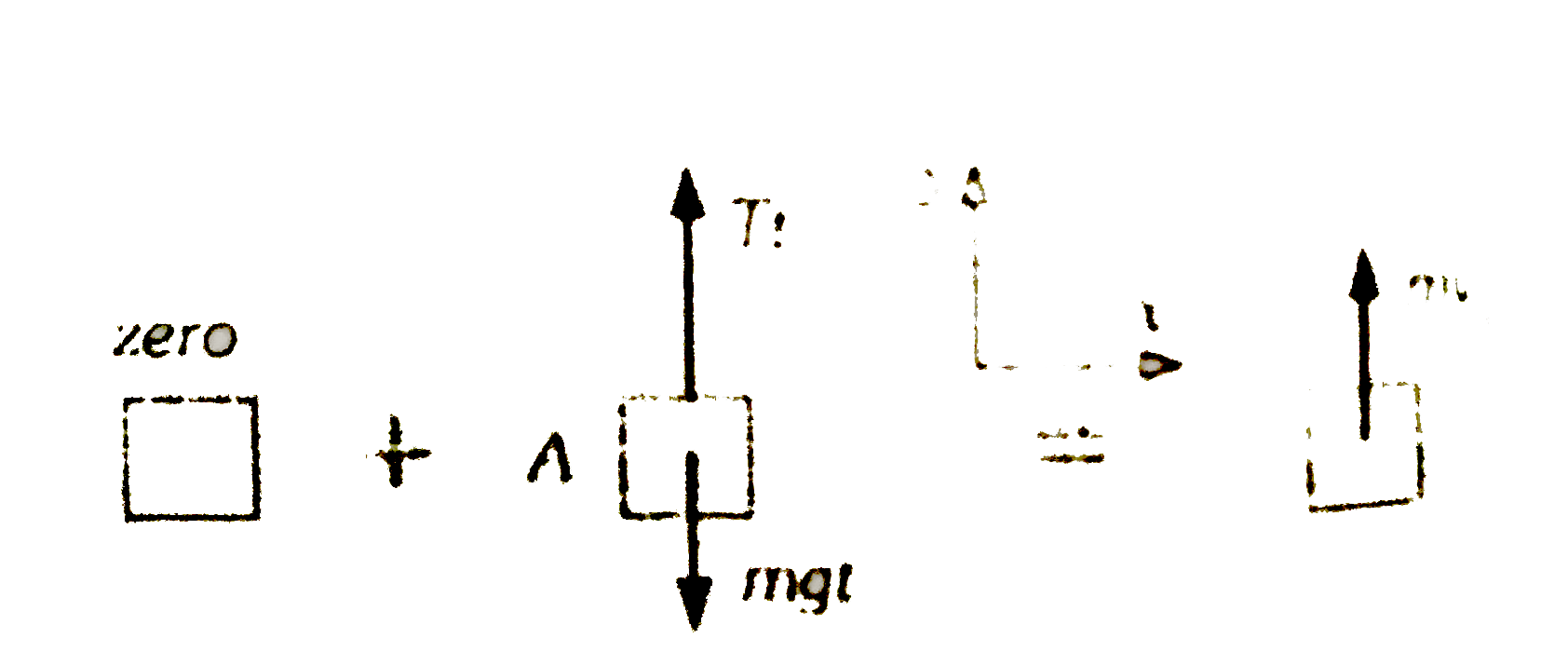
Applying impulse momentum principle to box B
P2y=p1y+∑Imp,y→ mvB=0+Mgt−2Tt ...(iii)

From equations (i), (ii) and(iii), we have
vA=2(M−2mM+4m)gt and vB=(M−2mM+4m)gt
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-I
Explore 40 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-II
Explore 43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
Two blocks of masses 2m and m are connected by a light string going over a pulley of mass 2m and radius R as shown in the figure. The system is released from rest. Find the angular momentum of system when the mass 2m has descended through a height h. Assume no slipping.

View SolutionTwo blocks A and B of masses m and M are attached with ideal string and pulley, and placed on smooth horizontal surface. Force F is applied horizontally as shown in figure. Find the ratio of the acceleration of A to that of B.

View Solution
Knowledge Check
Two blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
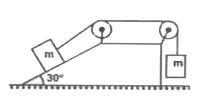 Ag/2Bg/4C2g/3D3g/4
Ag/2Bg/4C2g/3D3g/4Two masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
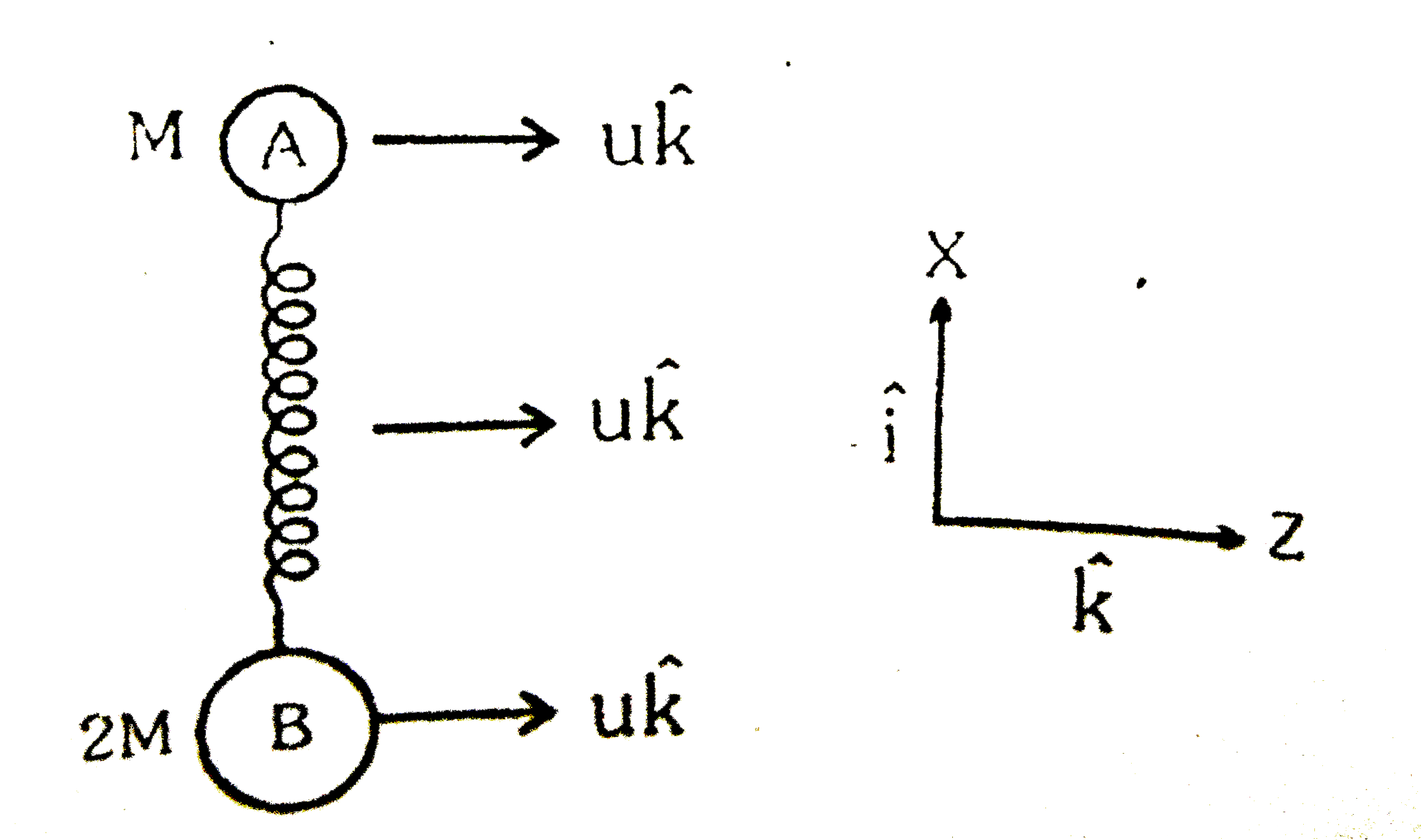 Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk
Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆkTwo unequal masses are connected on two sides of a light and smooth pulley as shown in figure. The system is released from rest. The larger mass is stopped 1.0 second after the system is set into motion and then released immediately. The time elapsed before the string is tight again is: Take g=10m/s2
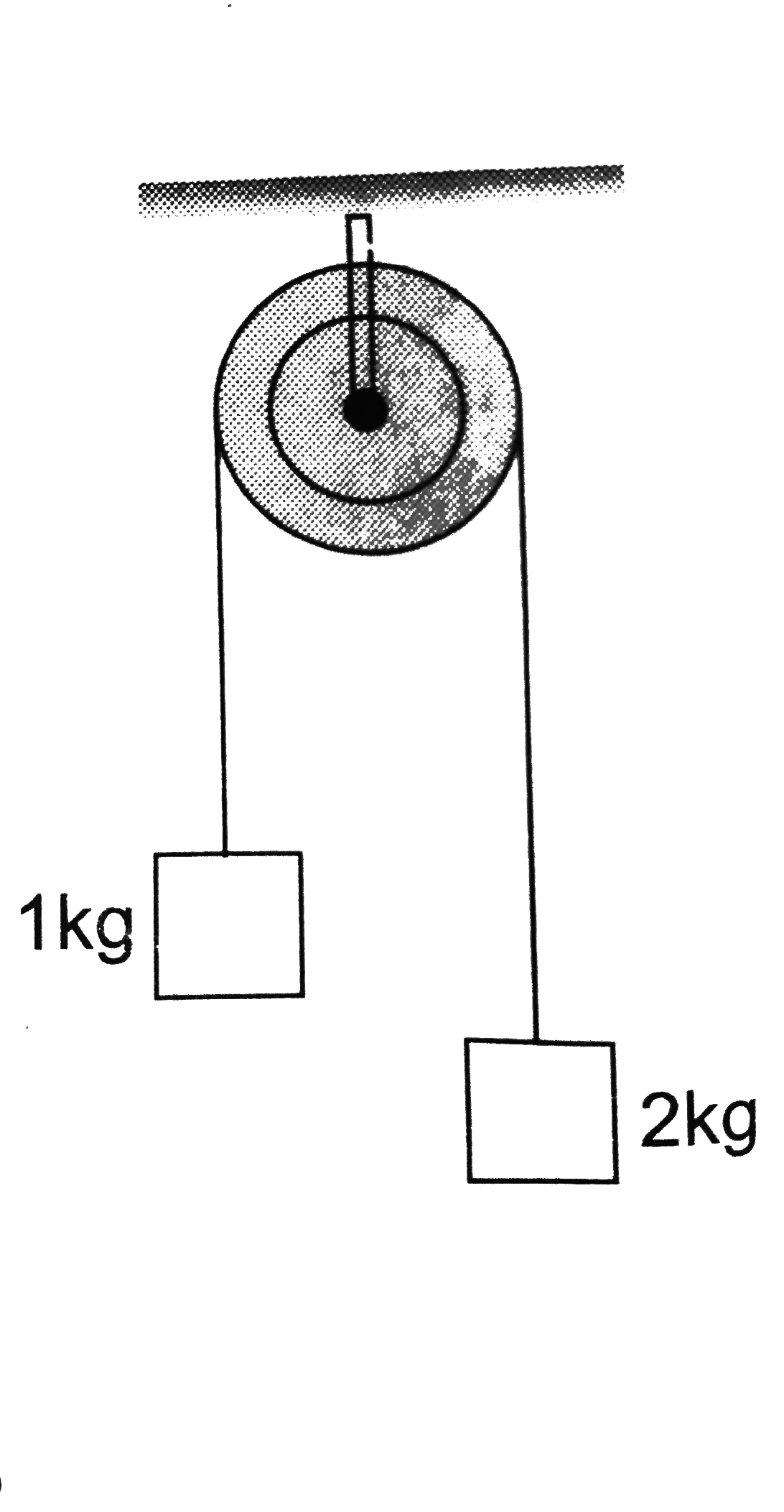 A1/4sB1/2sC2/3sD1/3s
A1/4sB1/2sC2/3sD1/3s
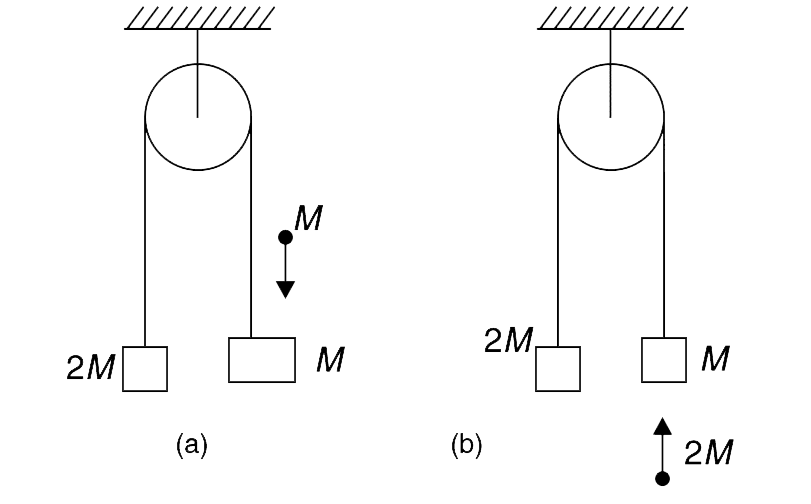
Two blocks of mass M and 2M are connected to the two ends of a light, inextensible string passing over an ideal pulley as shown in figure. The system is released from rest.
(a) One second after the system is released, a particle of mass M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling downward. Find the total distance travelled by block of mass 2M after it is released.
(b) One second after the system is released, a particle of mass 2M hits the block of mass M and sticks to it. The particle hits the block with a speed of 10 m/s while travelling in upward direction. Find distance travelled by the block of mass 2M after it is released to the time it comes to rest for the first time (g=10m/s)2
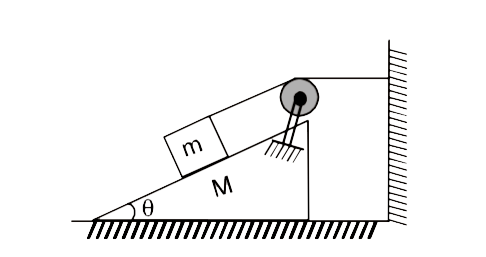
View SolutionFor the arrangement shown in figure when the system is released, find the acceleration of wedge. Pulley and string are ideal and friction is absent.
View SolutionTwo blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

View SolutionIn the figure shown, the system is released frrom rest. Find the velocity of block A when block B has fallen a distance l. Assume all pulleys to be massless and frictionless.

View SolutionIn the system shown in figure, the block A is released from rest. Find
the acceleration of both blocks ‘A’ and ‘B’.
View Solution
