
The figure shows a constant deviation prism ABCD. The incident ray is PQ and the emergent ray is ST. Although it is made up of one piece of glass, but it is equivalent to two 30∘−60∘−90∘ prism and one 45∘−45∘90∘ prism.The angle θ1 is the angle of incidence on face AB. The path of the ray inside the prism is indicated in the figure. for this prism μ=2sinθ1.
Q. The ratio θ1θ2 is
12
1
23
13
The correct Answer is:A
let r be angle of refraction at θ1
μ=sinθ1sinr,sinθ1=μ2⇒sinr=12,r=30∘
considering ABC as a triangular prism r+r′=A
30∘+r′=75∘⇒r′=45∘
Thus ray is incident on AB at 45∘ it is reflected at the same angle on to CD.
From the figure ∠RSD=360∘−(45∘+135∘+60∘)=120∘
(considering the quadrilateral)
∵ angle of incidence at CD=120∘−90∘=30∘
⇒θ1=θ2
∵ total deviation of ray =(θ1−30∘)+(180∘−90∘)−(θ2−30∘)=90∘
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Pt-02
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 107 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
The angle between the incident ray and the emergent ray in a glass prism is called (angle of incidence/angle of deviation).
View SolutionA ray of light falls on a glass prism at a angle of incidence of 30∘. Find the direction of the emergent ray if the angle of the prism is 60∘ and refractive index is 1.50
View Solution
Knowledge Check
Read the paragraph and the figure carefully and answer the questions.

The figure shows a constant deviation prism ABCD. The incident ray is PQ and the emergent ray is ST. Although it is made up of one piece of glass, it is equivalent to two 30∘−60∘−90∘ prisms and one 45∘−45−90∘ prism. The angle θ1 is the angle of incidence on face AB. The path of the ray inside the prism is indicated in the figure.
For this prism, μ=2sinθ1
The ratio of θ1θ2 isA1B12C√2D1√2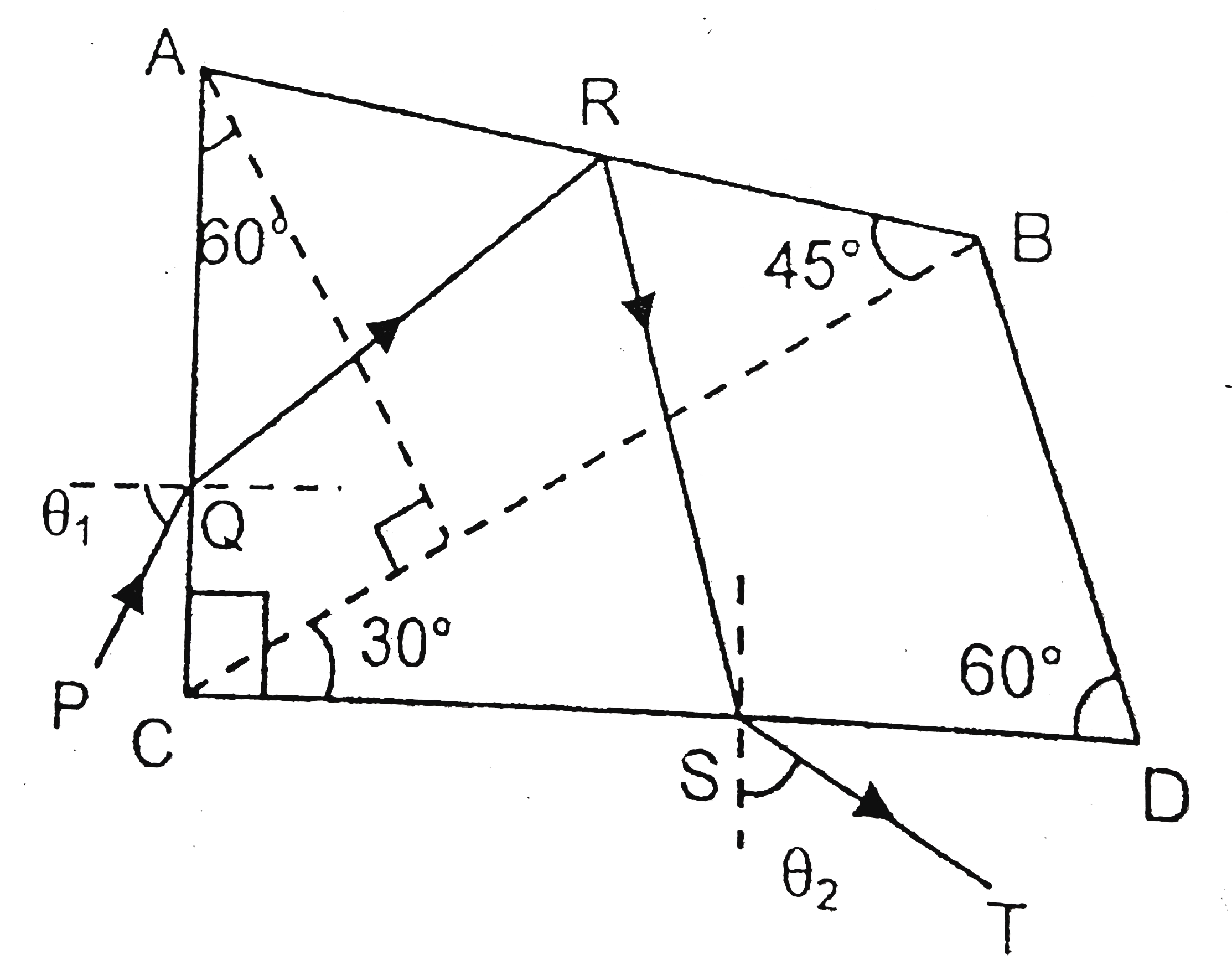
The figure shows a constant deviation prism ABCD. The incident ray is PQ and the emergent ray is ST. Although it is made up of one piece of glass, but it is equivalent to two 30∘−60∘−90∘ prism and one 45∘−45∘90∘ prism.The angle θ1 is the angle of incidence on face AB. The path of the ray inside the prism is indicated in the figure. for this prism μ=2sinθ1.
Q. The total deviation of incident ray when it emerges out of the prism isA60∘B30∘C45∘D90∘Read the paragraph and the figure carefully and answer the questions.

The figure shows a constant deviation prism ABCD. The incident ray is PQ and the emergent ray is ST. Although it is made up of one piece of glass, it is equivalent to two 30∘−60∘−90∘ prisms and one 45∘−45−90∘ prism. The angle θ1 is the angle of incidence on face AB. The path of the ray inside the prism is indicated in the figure.
For this prism, μ=2sinθ1
The angle of refraction on the face AB isA30∘B45∘C15∘D40∘
Read the paragraph and the figure carefully and answer the questions.

The figure shows a constant deviation prism ABCD. The incident ray is PQ and the emergent ray is ST. Although it is made up of one piece of glass, it is equivalent to two 30∘−60∘−90∘ prisms and one 45∘−45−90∘ prism. The angle θ1 is the angle of incidence on face AB. The path of the ray inside the prism is indicated in the figure.
For this prism, μ=2sinθ1
The total deviation of the incident ray when it emerges out of the prism is
View SolutionFigure shows graph of deviation δ versus angle of incidence for a light ray striking a prism. Angle of prism is

View SolutionA thin prism deviates an incident ray by 3.2∘. If the refractive index of the prism is 2.6 then the angle of prism is
View SolutionFigure shows the graph of angle of deviation ∂ versus angle of incidence i for a light ray striking a prism. The prism angle is

View SolutionA ray of light undergoes deviation of 30∘ when incident on an equilateral prism of refractive index √2. The angle made by the ray inside the prism with the base of the prism is
View Solution

