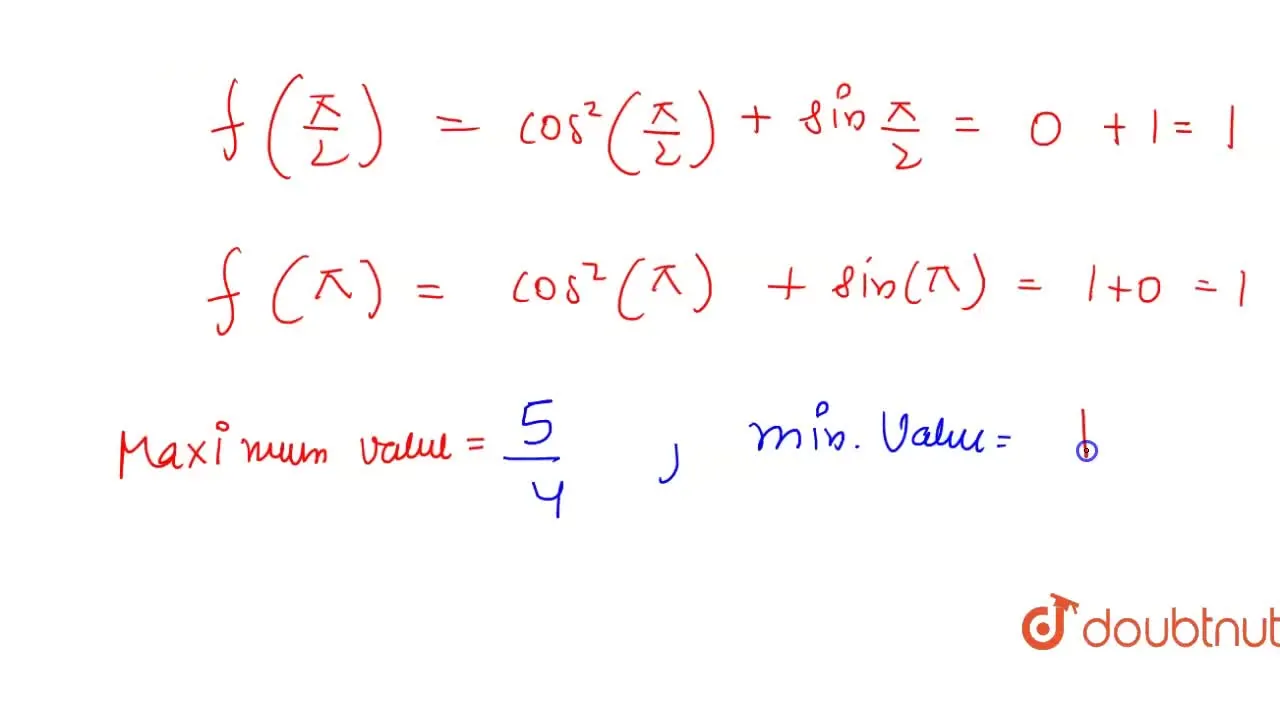Find the absolute maximum and minimum values of the function f given by f(x)=cos2x+sinx , x∈[0, π] .
f(x)=cos2x+sinx
f'(x)=−2cosxsinx+cosx
Critical points
f'(x)=−2cosxsinx+cos=0
⇒−2cosxsinx+cosx=0
⇒cosx(2sinx−1)
⇒x=π6 or π2
⇒−2cosxsinx+cosx=0
⇒cosx(2sinx−1)
⇒{x}=π6 or π2
f(π6)=cos2(π6)+sin(π6)=54
{f}(π2)=cos2(π2)+sin(π2)=1
f(0)=cos2(0)+sin(0)=1
f(π)=cos2(π)+sin(π)=1
maxima at x=π6
minima at x=π2,0,π
Related Playlists
Similar Questions
Find the absolute maximum and minimum values of the function f given by f(x)=cos2x+sinx , x∈[0, π] .
View SolutionFind the absolute maximum and minimum values of the function f given by f(x)=cos2x+sinx,x∈[0,π]
View SolutionFind the absolute maximum and the absolute minimum value of the function given by :
f(x)=sin2x−cosx,x∈[0,π].View SolutionFind the maximum and minimum values , if any , of the function f given by f(x)=3−|x|
View SolutionFind the maximum and minimum values of the function f(x)=tanx−2x .
View SolutionFind the maximum and minimum value if any , of the function f given by f(x)=x6−5.
View SolutionFind the maximum and minimum value if any , of the function f given by f(x)=5−|x−1|.
View SolutionFind the maximum and minimum values of any of the function f given by f(x)=x4,x∈R .
View SolutionFind the maximum and minimum values of the function f(x)=sinx+cos2x.
View SolutionFind the maximum and minimum values of f , if any, of the function given by f(x)=|x|,x∈R.
View Solution