Tangent to the circle x2+y2=a2 at any point on it in the first quadrant makes intercepts OA and OB on x and y axes respectively, O being the centre of the circle. Find the minimum value of OA+OB .
To find the minimum value of OA+OB where OA and OB are the intercepts made by the tangent to the circle x2+y2=a2 at a point in the first quadrant, we can follow these steps:
Step 1: Identify the point on the circle
Let the point P on the circle in the first quadrant be represented in parametric form as:
P=(acosθ,asinθ)
where θ is the angle made with the positive x-axis.
Step 2: Write the equation of the tangent line
The equation of the tangent line to the circle at point P(x1,y1) is given by:
xx1+yy1=a2
Substituting x1=acosθ and y1=asinθ, we get:
x(acosθ)+y(asinθ)=a2
Dividing through by a (since a≠0):
xcosθ+ysinθ=a
Step 3: Find the intercepts OA and OB
To find the x-intercept OA, set y=0:
xcosθ=a⟹OA=acosθ
To find the y-intercept OB, set x=0:
ysinθ=a⟹OB=asinθ
Step 4: Express OA+OB
Now, we can express OA+OB:
OA+OB=acosθ+asinθ=a(1cosθ+1sinθ)
This can be rewritten as:
OA+OB=a(sinθ+cosθsinθcosθ)
Step 5: Minimize OA+OB
To minimize OA+OB, we need to minimize:
f(θ)=sinθ+cosθ
To find the critical points, we differentiate f(θ):
f′(θ)=cosθ−sinθ
Setting the derivative to zero:
cosθ−sinθ=0⟹tanθ=1⟹θ=π4
Step 6: Calculate the minimum value
Substituting θ=π4 back into OA+OB:
OA+OB=a(1cosπ4+1sinπ4)=a⎛⎜⎝11√2+11√2⎞⎟⎠=a(√2+√2)=2√2a
Conclusion
Thus, the minimum value of OA+OB is:
2√2a
Let the point P on the circle in the first quadrant be represented in parametric form as:
P=(acosθ,asinθ)
where θ is the angle made with the positive x-axis.
The equation of the tangent line to the circle at point P(x1,y1) is given by:
xx1+yy1=a2
Substituting x1=acosθ and y1=asinθ, we get:
x(acosθ)+y(asinθ)=a2
Dividing through by a (since a≠0):
xcosθ+ysinθ=a
To find the x-intercept OA, set y=0:
xcosθ=a⟹OA=acosθ
To find the y-intercept OB, set x=0:
ysinθ=a⟹OB=asinθ
Now, we can express OA+OB:
OA+OB=acosθ+asinθ=a(1cosθ+1sinθ)
This can be rewritten as:
OA+OB=a(sinθ+cosθsinθcosθ)
To minimize OA+OB, we need to minimize:
f(θ)=sinθ+cosθ
To find the critical points, we differentiate f(θ):
f′(θ)=cosθ−sinθ
Setting the derivative to zero:
cosθ−sinθ=0⟹tanθ=1⟹θ=π4
Substituting θ=π4 back into OA+OB:
OA+OB=a(1cosπ4+1sinπ4)=a⎛⎜⎝11√2+11√2⎞⎟⎠=a(√2+√2)=2√2a
Thus, the minimum value of OA+OB is:
2√2a
Topper's Solved these Questions
Similar Questions
Tangent to the circle x2+y2=a2 at any point on it in the first quadrant makes intercepts OA and OB on x and y axes respectively, O being the centre of the circle. Find the minimum value of OA+OB .
View SolutionTangent to the circle x2+y2=4 at any point on it in the first quadrant makes intercept OA and OB on x axis and y axis respectively.O being the center of circle. Find the minimum value of OA+OB
View Solution
Knowledge Check
If O is the centre of the circle, then x is
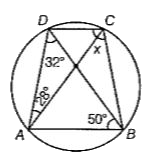 A72∘B62∘C82∘D52∘
A72∘B62∘C82∘D52∘If O is the centre of the circle, then x is
 A72∘B62∘C82∘D52∘
A72∘B62∘C82∘D52∘In the given figure, O is the centre of the circle. The value of x is
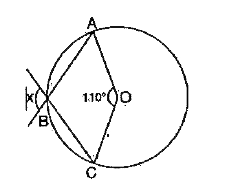 A75∘B55∘C125∘D110∘
A75∘B55∘C125∘D110∘
In Figure, O is the centre of the circle. If ∠BOD=1600, find the values of x and y
View SolutionTangent to the circle x2+y2=16 at the point (2,2√3) makes intercepts a and b on x and y-axes, then ab=?
View SolutionO is the centre of the circle ∠BCO=30∘ then find x and y
View SolutionO is the centre of the circle x and y respectively equal.

View SolutionGiven that AOB is a straight line and O is the centre of the circle. Find the value of y.

View Solution

