y(x,t)=0.8/[4x+5t)2+5] represents a moving pulse, where x and y are in meter and t in second. Then
pulse is moving in positive x-direction
in 2 s it will travel a distance of 2.5 m
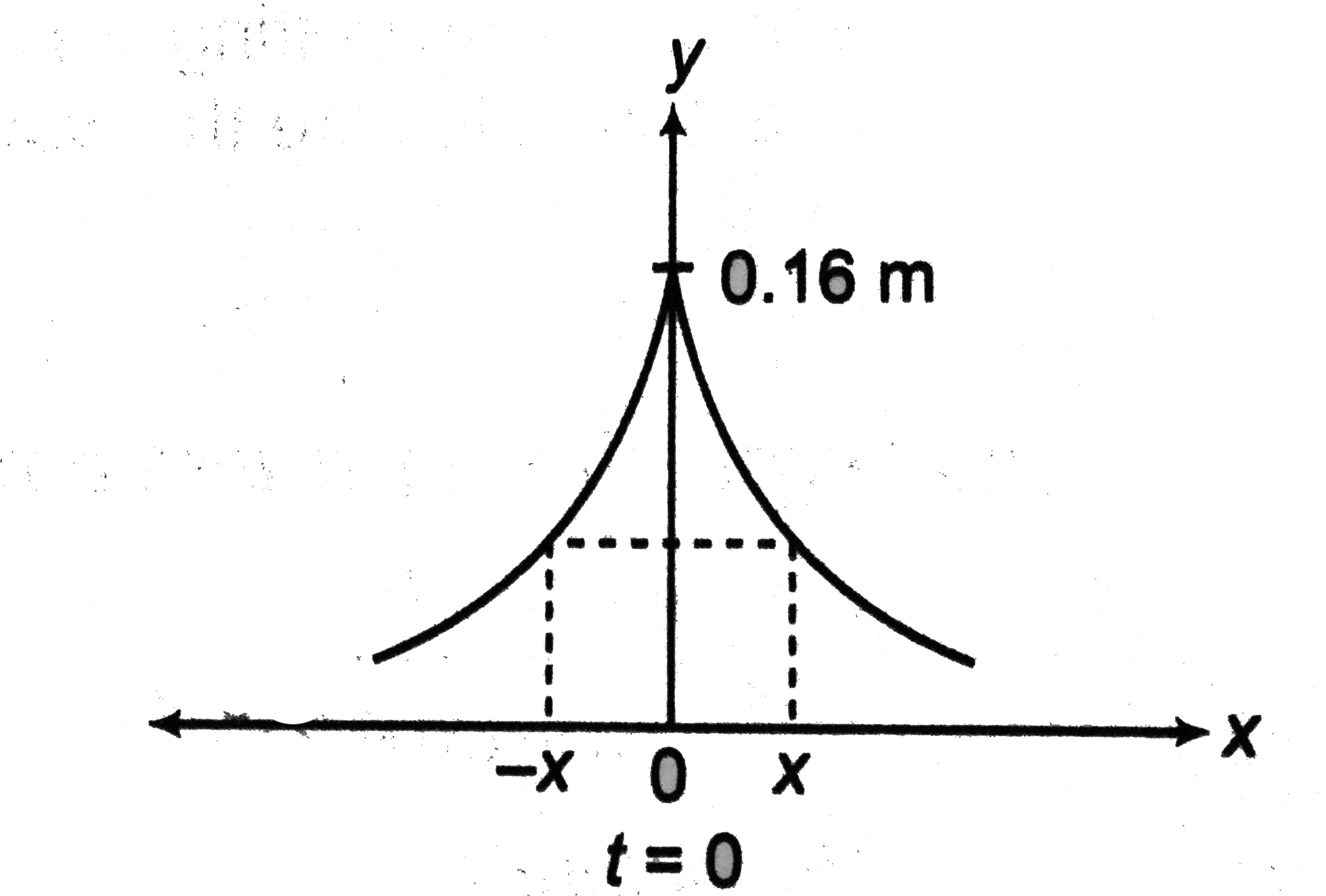
Its maximum displacment is 0.16 m
it is a symmetric pulse
The correct Answer is:B, C, D
The shape of pulse at x = 0 and t = 0 would be as shown, in figure (a)
y=(0,0)=0.85=0.16m
_E01_194_S01.png)
from the figure it is clear that ymax=0.16m
Pulse will be symmetric (Symmetric is checked about ymax) if t = 0
y (x) = y(x)
From the given equation and
y(x)=0.816x2+5y(−x)=0.816x2+5⎫⎪⎬⎪⎭att=0⇒y(x)=y(x)
Therefore, pulse is symmetric
Speed of pulse
At t = 1s and x = 1.25 m
_E01_194_S02.png)
value of y is given 0.16 m, i.e. pulse has travelled a distance of 1.25 m in 1s negative x-direction or we can say that the speed of pulse is 1.25 m/s and it is travelling in negative x-direction. Therefore, it will travel a distance of 2.5 m in 2s.
The above statement can be better understood from figure (b).
Topper's Solved these Questions
Similar Questions
y(x,t)=0.8[(4x+5t)2+5] represents a moving pulse where x and y are in metre and t in second. Then,choose the correct alternative(s):
(a) pules is moving in positive x- direction
(b) in 2s it will travel a distance of 2.5m
(c) its maximum displacement is 0.16m
(d) it is a sysmmetric pulse
View Solutionx(x,t)=0.8[(4x+5t)2+5], represents a moving pulse where x and y are in metre and t is in second. Find
(i) The direction of wave propagation.
(ii) The wave speed.
(iii) The maximum displacement from the mean position (i.e., the aplitude of the wave).
(iv). Whether the wave pulse is symmetric or not.
View Solution
Knowledge Check
x(x,t)=0.8[(4x+5t)2+5], represents a moving pulse where x and y are in metre and t is in second. Find
(i) The direction of wave propagation.
(ii) The wave speed.
(iii) The maximum displacement from the mean position (i.e., the aplitude of the wave).
(iv). Whether the wave pulse is symmetric or not.APulse is moving in +x direction.BIn two seconds it will travel a distance of 2.5 mCIt's maximum displacement is 0.16 mDIt's a symmetric pulse.y(x,t)=1.0[(ax+bt)2+(cx+dt)2+5] represents a moving pulse where x and y are in metres and t in seconds. It has speed of pulse b/a. Find the correct option.
Abc=adBbd=acCab=cdDnone of theseThe x and y coordinates of the particle at any time are x=5t−2t2andy=10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
A5m/s2B−4m/s2C−8m/s2D0
The vertical and horizontal displacements of a projectile thrown from a point on the ground at time t are given by y=6t−5t2 and x=8t respectively,where x and y are in meters and t is in seconds.The time of flight of the projectile in seconds is ?
View SolutionThe x and y coordinates of the particle at any time are x=5t−2t2 and y = 10t respectively, where x andy are in metres and / in seconds. The acceleration of the particle at t = 5 s is
View SolutionThe x and y coordinates of a particle at any time t is given by x=7t+4t2 and y=5t, where x and y are in metre and t in seconds. The acceleration of particle at t=5s is
View SolutionThe x and y coordinates of a particle at any time t are given by x=2t+4t2andy=5t , where x and y are in metre and t in second. The acceleration of the particle at t = 5 s is
View SolutionThe x and y coordinates of the particle at any time are x=5t−2t2andy=10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t=2s is:
View Solution
