One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
y(t)=Asin(πx)6cos(50πt)3
y(t)=Asin(πx)3cos(100πt)3
y(t)=Asin(5πx)6cos(250πt)3
y(t)=Asin(5πx)2cos250πt
The correct Answer is:A, C, D
At x=0y=0x=3y=0ωk=100m/s⎤⎥
⎥⎦
The equation satisfying all three conditions is correct.
Topper's Solved these Questions
Similar Questions
The speed of a transverse wave in a stretched string is 348 ms−1, when the tension of the string is 3.6 kg wt. Calculate the speed of the transverse wave in the same string . If the tension in the string is changed to 4.9 kg wt ?
View Solution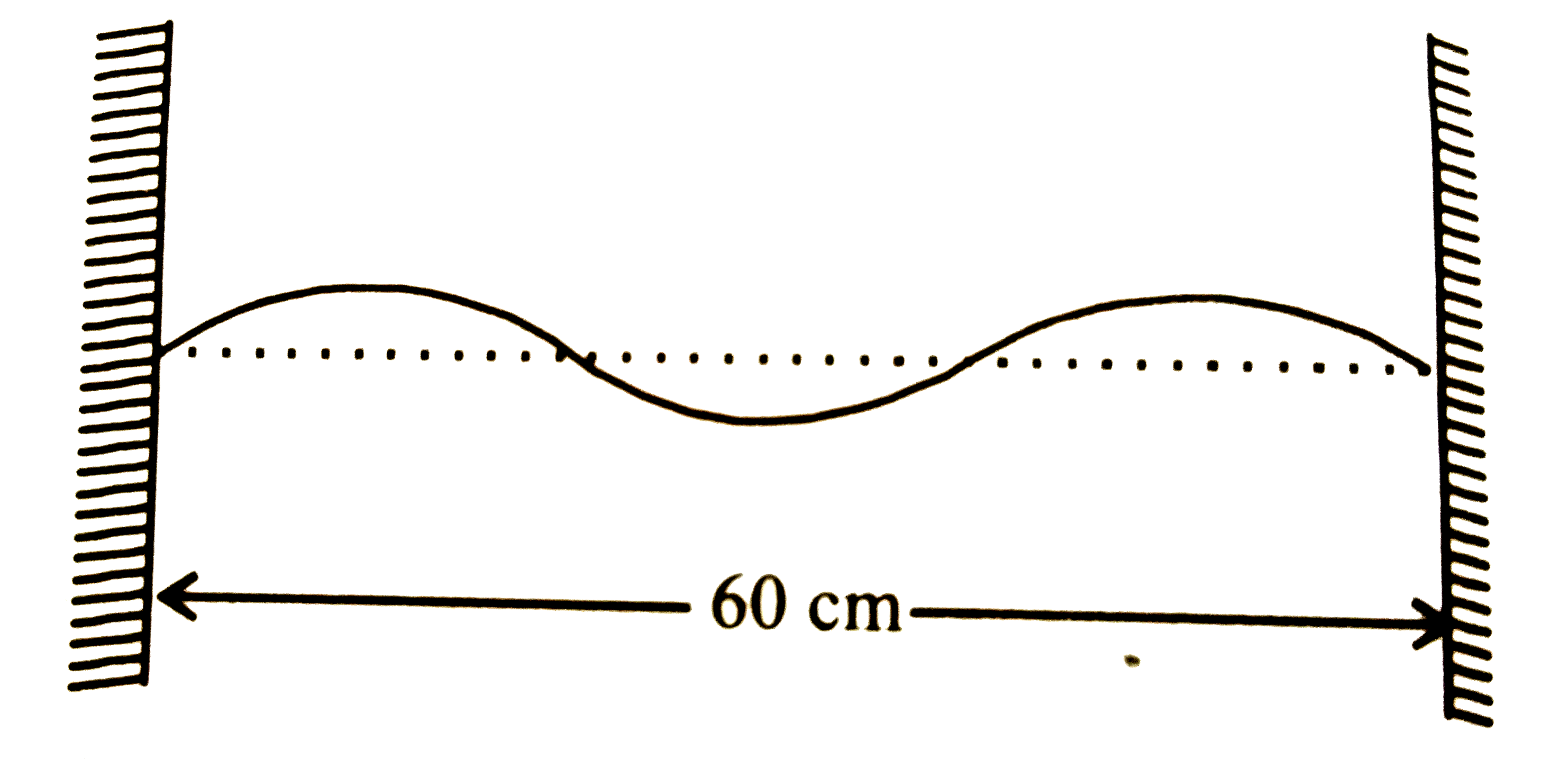
The standing wave pattern along a string of length 60 cm is shown in the above diagram. If the speed of the transverse waves on this string is 300 m/s, in which one of the following modes is the string vibrating?
View Solution
Knowledge Check
A string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
A77m/sB102m/sC110m/sD165m/sThe maximum or thershold wavelength of transverse stationary wave on a string of length l is
AlB2lCl2D4lA stretched string is fixed at both its ends. Three possible wavelengths of stationary wave patterns that can be set up in the string are 90 cm, 60 cm and 45 cm. the length of the string may be
A80 cmB120 cmC90 cmD45 cm
A string of 2 m length is fixed at both the ends . The transverse wave created in it propogates with a speed of 50ms−1 . If the string is made to vibrate with three loops , find the frequency of the wave produced .
View SolutionA string of length L and mass M hangs freely from a fixed point. Then the velocity of transverse waves along the string at a distance x from the free end is
View SolutionThe displacement of a vibrating string versus position along the string is shown in the figure. The periodic wave have a speed of 10.0cm/s. A and B are two points on the string.
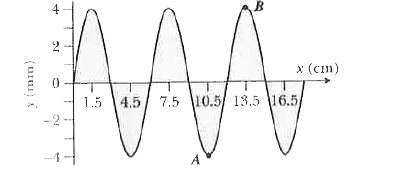
What is the wavelength of the wave?
View SolutionA string fixed at both the ends is vibrating in two segments. The wavelength of the corresponding wave is
View SolutionA stretched string of length L , fixed at both ends can sustain stationary waves of wavelength λ Which of the following value of wavelength is not possible ?
View Solution

