Statement-1: if moment of inertia of a rigid body is equal about two axis, then both the axis must be parallel.
Statement-2 from parallel axis theorem I=Icm+md2, where all terms have usual meaning.
Statement-1 is true, Statement-2: is true, Statement-2 is a correct explanation for Statement-1.
Statement-1 is true, Statement-2: is true, Statement-2 is NOT a correct explanation for Statement-1.
Statement-1 is true but statement-2 is false
Both statement 1 false and statement 2 are true.
The correct Answer is:D
For a uniform solid sphere moment of inertia about any axis passing through centre is same. All this axis are not parallel. Hence Statement-1 is false, Statement-2 is True.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Assertion: Moment of inertia of a rigid body about any axis passing through its centre of mass is minimum
Reason: From theorem of parallel axis
I=Icm+Mr2AIf both Assertion and Reason are true and the Reason is correct explanation of the Assertion.BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion.CIf assertion is true, but the reaction is false.DIf assertion is false but the reason is true.Consider a semicircular ring with mass m and radius R as shown in figure.
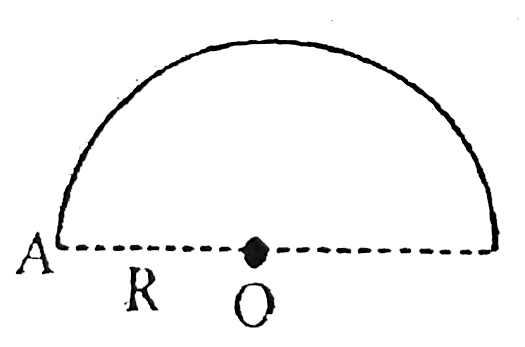
Statement-1: The moment of inertia of semi - circular ring about an axis passing through A and perpendicular to plane is 2mR2
Statement-2: According to parallel axis theorem: IA=1cm+mR2AStatement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.BStatement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.CStatement-1 is true, statement-2 is false.DStatement -1 is false, statement -2 is true.The moment of inertia of a ring of mass 5 gram and radius 1 cm about and axis passing through its edge and parallel to its natural axis is
A5g−cm2B2.5 g - cm2C20 g - cm2D10 g - cm2
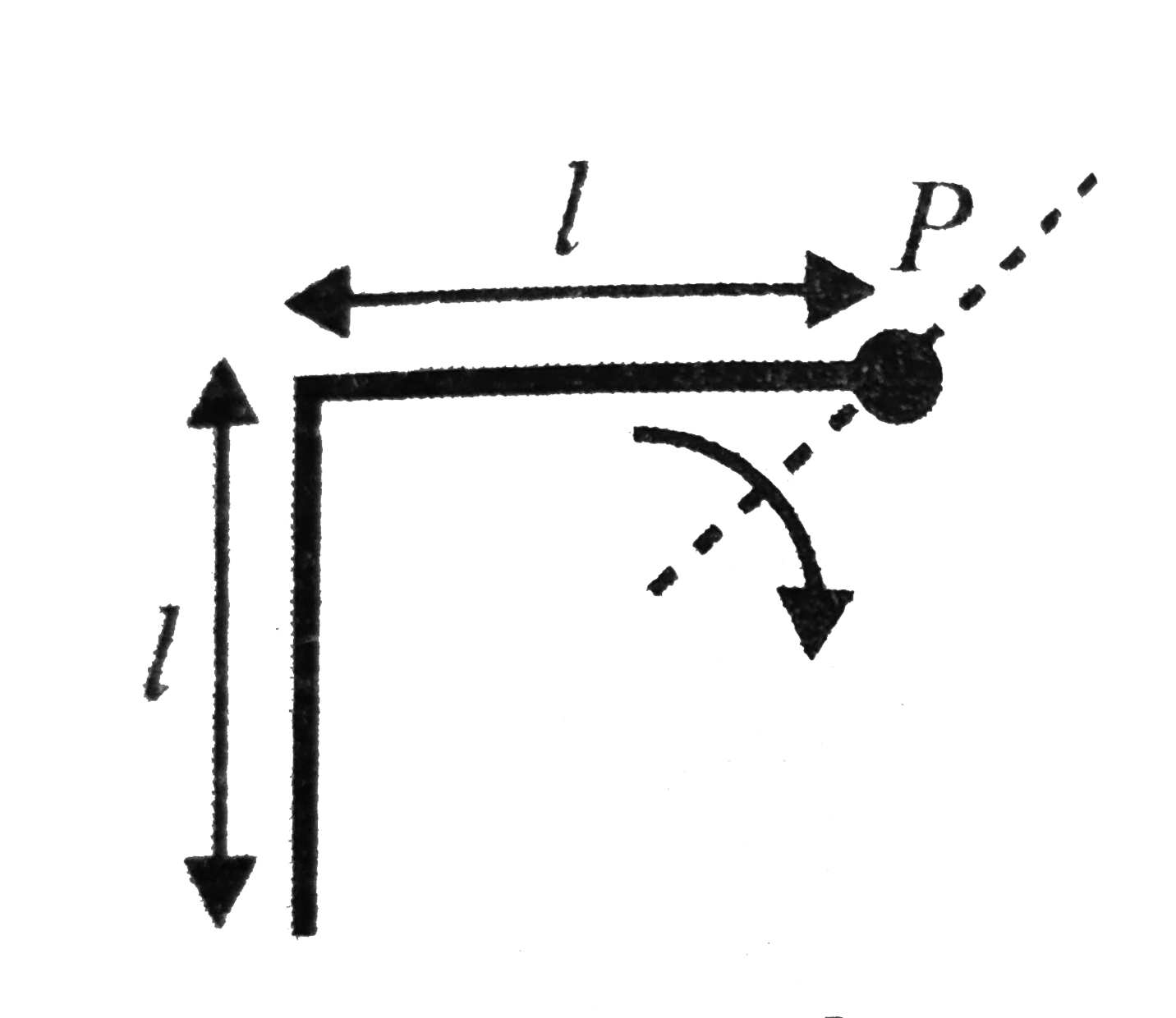
Find the moment of inertia of the two uniform joint rods about point P as shown in Fig. Use parallel axis theorem. Mass of each rod is M.
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis tangent to the disc and parallel to its diameter
View SolutionStatement-1 : Moment of inertia of a body is same, whatever be the axis of rotation.
Statement-2 : Moment of inertia depends on mass and size of rotation of the body.
View SolutionMoment of inertia I of a solid sphere about an axis parallel to a diameter and at a distance x from it varies as:
View SolutionMoment of inertia of a disc of radius R about a diametric axis is 35kg m−2. The MI of the disc about a parallel axis at a distance R/2 from the centre is
View Solution