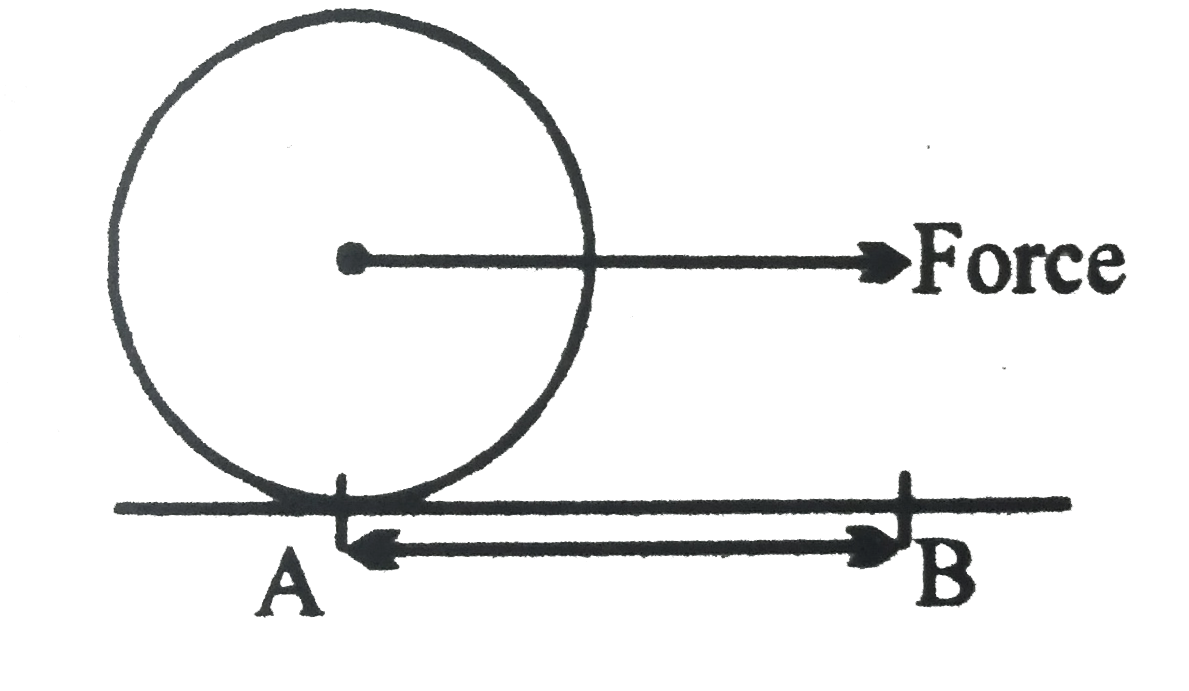
A disc of circumference is at rest at a point on a horizontal surface when a constant horizontal force begins to act on its centre. Between and there is sufficient friction toprevent slipping, and the surface is smooth to the right of . The disc moves from to in time . To the right of ,
 .
.
the angular acceleration of the disc will disappear, linear acceleration will remain unchanged
linear acceleration of the disc will increase
the disc will make one rotation in time T/2
the disc will cover a distance greater then s in further time T.
The correct Answer is:A
To the right of B the friction force will disppear so , linear acc. Increases so disc cover distance greater than s in time T to the right of B the is maximum and in one revolution will complete
Topper's Solved these Questions
Similar Questions
A disc of circumference S stands vertically on a horizontal surface as shown in figure-5.145, A horizontal force P acts on the centre of the disc. Half of the circumference {ABC) is rough and the friction is sufficient to prevent slipping when the disc rolls along X¥.The other half of the circumference (ADC) is smooth. The disc starts from rest when P begins to act and the point C is at the bottom. Find the distance moved by the disc along xy when it completes one rotation.
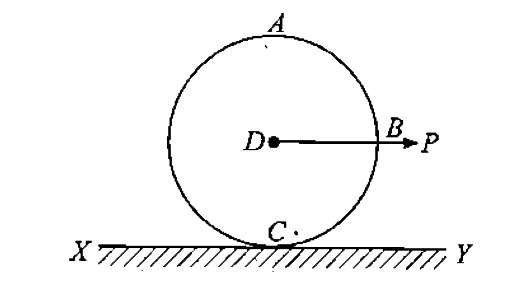
View SolutionA constant horizontal force F acts on a solid circular disc (M, R) as shown. The disc rolls without slipping, even on smooth surface for x=Rn . Value of n is?
View Solution
Knowledge Check
A particle initially at rest on a smooth horizontal surface, is acted on by a constant horizontal force at time t=0 then if W= work, done t=time and v=speed of the particle, the nearly correct graph (s) is //are
A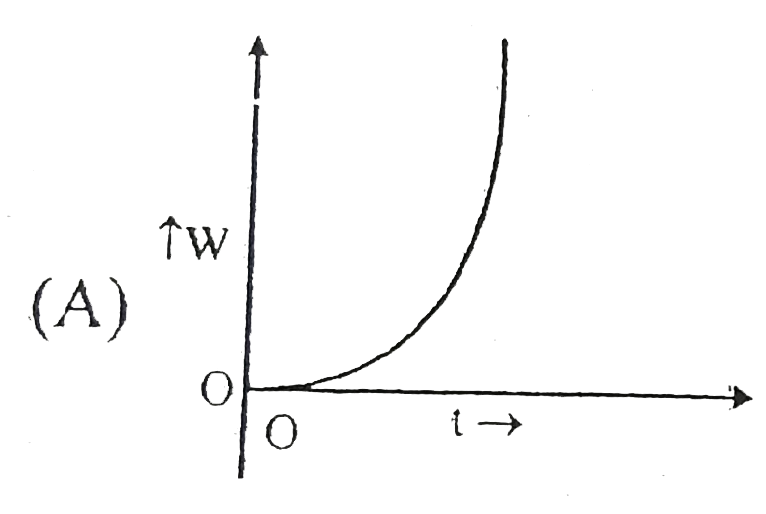 B
B C
C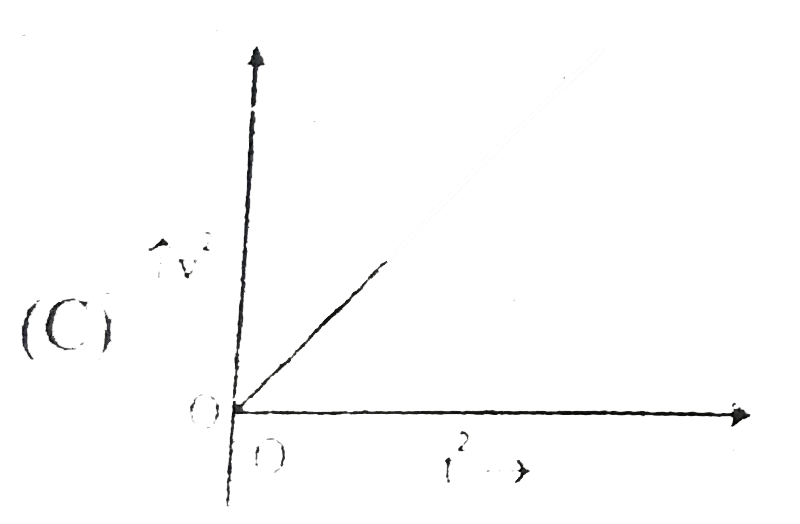 D
D
A uniform disc is rolling on a horizontal surface. At a certain instant B is the point of contact and A is at height 2R from ground, where R is radius of disc -
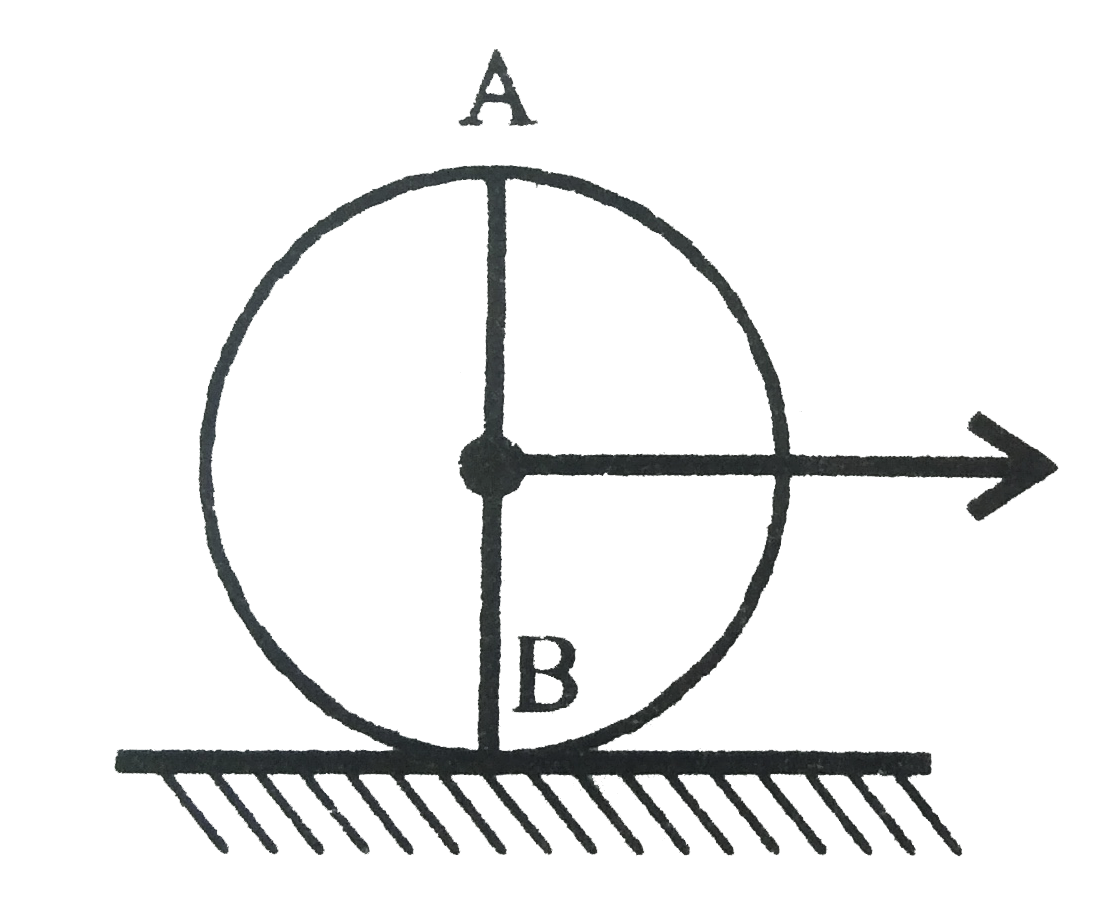 .AThe magnitude of the angular momentum of the disc about
.AThe magnitude of the angular momentum of the disc about
b is thrice that about ABThe angular momentum of the disc about A anticlockwiseCThe angular momentum of the disc about B is clockwiseDThe angular momentum of the disc about about A is equal to that about B.A block 'B' rests on 'A' A rests on a horizontal surface 'C' which is frictionless. There is friction between A and B If 'B' pulled to the right .
AB moves forward and A to the leftB'B' only moves to the leftCB' does not moveD'A' and 'B' move together to the right .
A disc of mass 100 g is rolling without slipping on a horizontal surface with a velocity of 10cms−1. Calculate its total energy.
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time
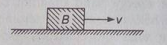
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time

View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionA disc of mass 2 kg is rolling on a horizontal surface without slipping with a velocity of 0.1 m/s. What is its rotational kinetic energy?
View Solution

