A small ball of radius r rolls without sliding in a big hemispherical bowl. of radius R. what would be the ratio of the translational and rotaional kinetic energies at the bottom of the bowl.

A

$2 : 1$

B

$3 : 2$

C

$4 : 3$

D

$5 : 2$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$\frac{K . E ._{T}}{K . E ._{R}} = \frac{\frac{1}{2} M v^{2}}{\frac{1}{2} I ω^{2}} = \frac{\frac{1}{2} M v^{2}}{\frac{1}{2} \frac{2}{5} M R^{2} {(\frac{v}{R})}^{2}} = 5 : 2$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A disc is rolling on a surface without slipping. What is the ratio of its translational to rotational kinetic energies ?
A $5 : 2$
B $1 : 1$
C $3 : 2$
D $2 : 3$
Question 2 - Select One or More
A small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere

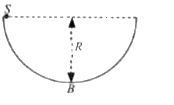AThe fraction of translational kinetic energy at the sphere is 5/7.
BThe fraction of rotational kinetic energy of the sphere is 2/7.
CThe fraction of rotational kinetic energy of the sphere is $\frac{2}{7} m v^{2}$ .
DThe total kinetic energy of the sphere at the bottom of the bowl is $\frac{2}{7} m v^{2}$
Question 3 - Select One
For a body rolling along a level surface, without slipping the translational and rotational kinetic energies are in the ratio $2 : 1$ . The body is
AHollow sphere
Bsolid cylinder
Cring
Dsolid sphere

RESONANCE-RIGID BODY DYNAMICS-Exercise

Home
Ask Doubt
Profile