Velocity of a particle of mass 2kg varies with time t according to the equation $\vec{v} = (2 t \hat{i} + 4 \hat{j}) m / s$ . Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.

A

$2 \hat{i} m / s$

B

$4 \hat{i} m / s$

C

$8 \hat{i} m / s$

D

$6 \hat{i} m / s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$v_{t = 0} = 4 h$ m/sec mass m=2kg
$v_{t = 2} = 2 \times 2 j + 4 j = 4 i + 4 j$
$J = P_{f} - P_{i} = 2 [4 i + 4 j - 4 j] = 8 i N - s$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In the figure the variations of componets of acceleration of particles of mass 1kg is shown w.r.t. time. The initial velocity of the particle is $\to u = (- 3 ˆ i + 4 ˆ j)$ m/s. the total work done by the resultant force on the particles in time intervals from t=0 to t=4 seconds is :

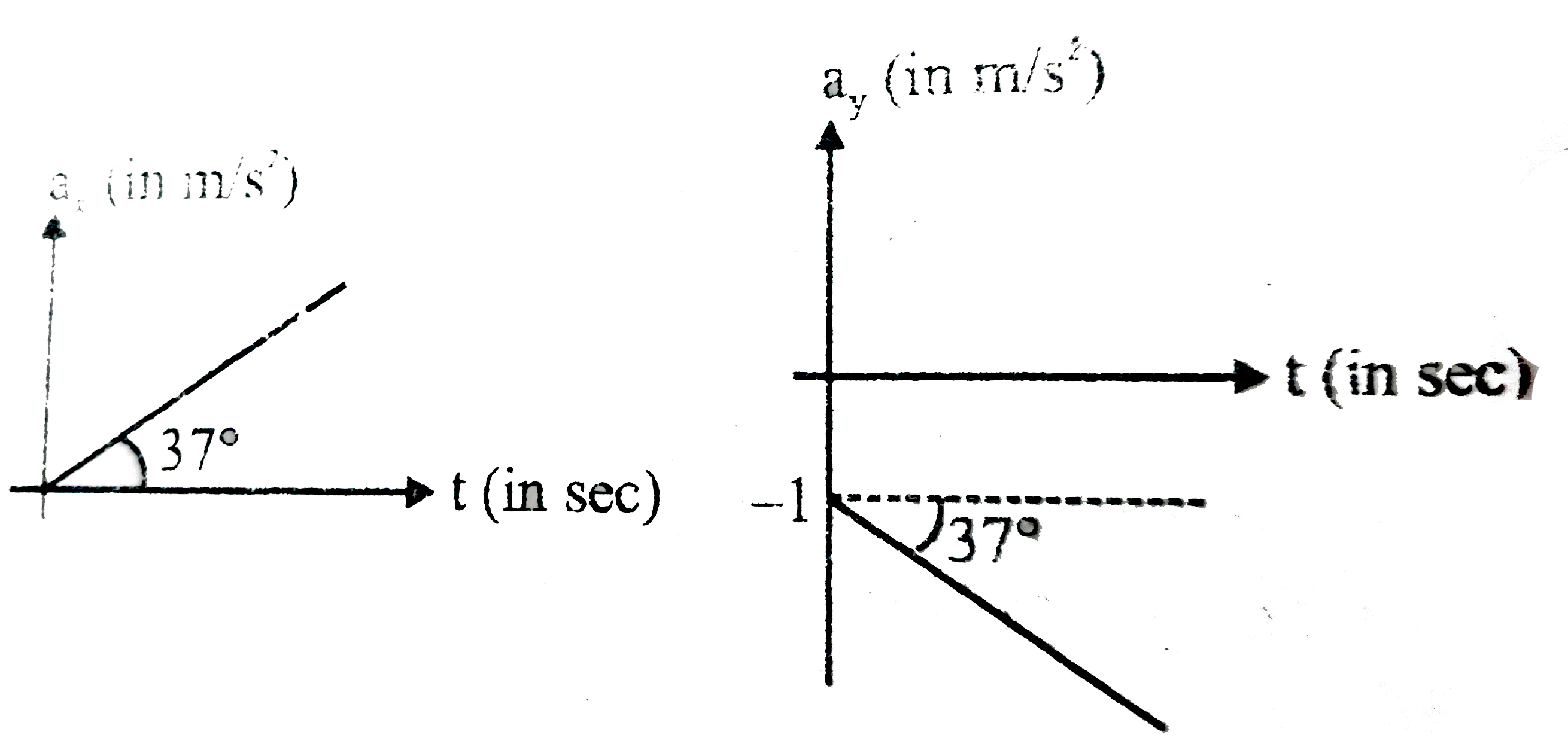A22.5J
B10 J
C0
DNone of these
Question 2 - Select One or More
Velocity of a particle moving in a curvilinear path varies with time as $v = (2 t ˆ i + t^{2} ˆ k) m / s$ . Here t is in second. At $t = 1$ s
Aacceleration of particle is $8 m / s^{2}$
Btangential acceleration of particle is $\frac{6}{\sqrt{5}} m / s^{2}$
Cradial acceleration of particle is $\frac{2}{\sqrt{5}} m / s^{2}$
Dradius of curvature to the path is $\frac{5 \sqrt{5}}{2} m$
Question 3 - Select One
A particle starts from rest with a time varying acceleration $a = (2 t - 4)$ . Here $t$ is in second and $a$ in $m / s^{2}$
The velocity time graph of the particle is
Aparabola passing through origin
Bstraight line not passing through origin
Cparabola not passing through origin
Dstraight line passing through origin

RESONANCE-CENTRE OF MASS-Exercise

Home
Ask Doubt
Profile