A particle starts moving rectilinearly at time such that its velocity changes with time according to the equation , where is in seconds and in . Find the time interval for which the particle retards.
Acceleration of the particle,
The particle retards when acceleration is oppostie to velocity. Hence, acceleration vector and velocity vector should be opposite to each other or the dot product of and should be negative.
is always positive.
Either or
and . This is not possible.
or and and . Hencec, the required time interval is .
Topper's Solved these Questions
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Solved Examples
Explore 9 Videos
- KINEMATICS-1Book:CENGAGE PHYSICSChapter:KINEMATICS-1Exercise:Exercise 4.1
Explore 17 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
- KINEMATICS-2Book:CENGAGE PHYSICSChapter:KINEMATICS-2Exercise:Exercise Integer
Explore 9 Videos
Similar Questions
A particle starts moving rectilinearly at time t=0 such that its velocity(v) changes with time (t) as per equation –
v=(t2–2t)m/s for 0<t<2s
=(–t2+6t–8)m/s for 2≤te4s
(a) Find the interval of time between t=0 and t=4s when particle is retarding.
(b) Find the maximum speed of the particle in the interval 0≤t≤4s.
View SolutionA particle moving in a straight line has its velocit varying with time according to relation v=t2−6t+8(m/s) where t is in seconds. The CORRECT statement(s) about motion of this particle is/are:-
View Solution
Knowledge Check
A particle starts moving rectilinearly at time t = 0 such that its velocity v changes with time t according to the equation v=t2−t, where t is in seconds and v is in ms−1. The time interval for which the particle retrads (i.e., magnitude of velocity decreases)is
At<1/2B1/2<t<1Ct>1Dt<1/2andt>1A particle starts moving rectillineraly at time t=0, such that its velocity 'v' changes with time 't' according to the equation v=t2−t where t is in seconds and v is in m/s. The time interval for which the particle retards is
At<1/2B1/2<t<1Ct>1Dt<1/2 and t>1Velocity of a particle of mass 2kg varies with time t according to the equation →v=(2tˆi+4ˆj)m/s. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
A2ˆim/sB4ˆim/sC8ˆim/sD6ˆim/s
A particle is moving along x-axis such that its velocity varies with time according to v=(3m/s2)t−(2m/s3)t2. Find the velocity at t = 1 s and average velocity of the particle for the interval t = 0 to t = 5 s.
View SolutionA particle moves on x-axis with a velocity which depends on time as per equation v=t2−8t+15(m/s) where time t is in seconds. Match the columns.
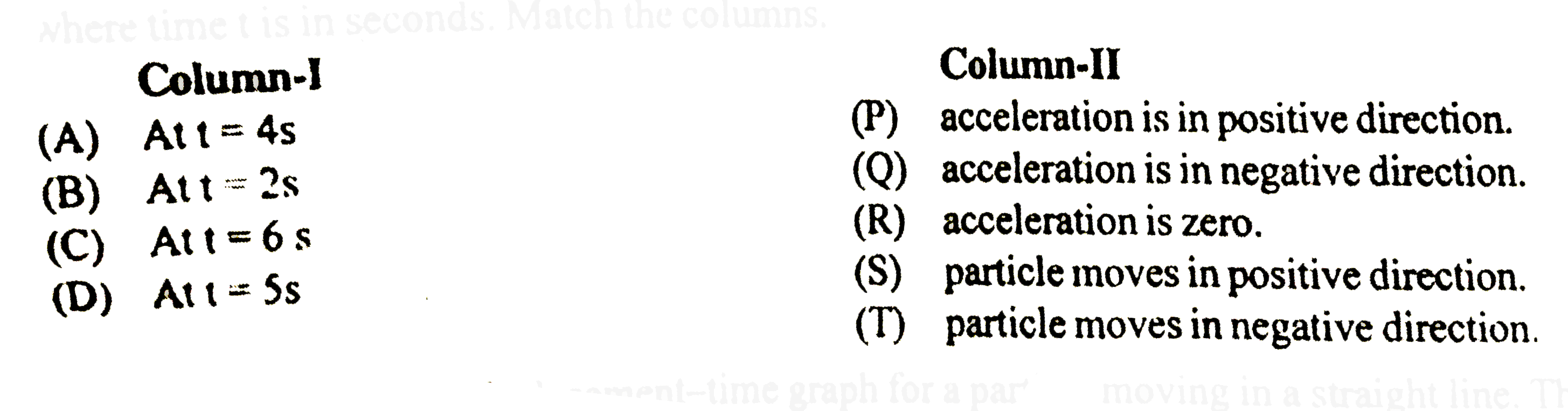
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=0 s to t=1 s.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
View Solution

