A particle of mass $m$ starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it break off the sphere ?

A

$\frac{2 g}{3}$

B

$\frac{\sqrt{5} g}{3}$

C

g

D

$\frac{g}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

at loose contact N=0
$m g cos θ = \frac{m v^{2}}{R} ... . . (1)$
from energy conservation
$m g R (1 - cos θ) = \frac{1}{2} m v^{2} ... ... (2)$
from (1) and (2)
$cos θ = \frac{2}{3} \Rightarrow sin θ = \frac{\sqrt{5}}{3}$
tangential acceleration $= g sin θ = \frac{\sqrt{5} g}{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS CIRCULAR MOTION

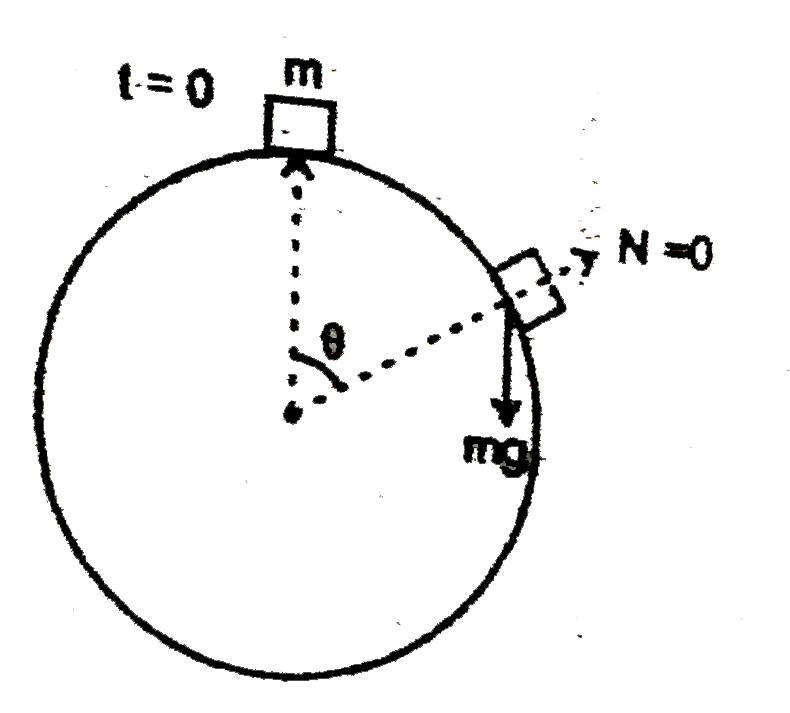
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m begins to slide down on a fixed smooth sphere from the top, when it breaks off the sphere, the tangential accleration will be
A $2 g / 3$
Bg
C $\frac{\sqrt{5}}{3} g$
D $\frac{g}{2}$
Question 2 - Select One or More
A particle of mass m is kept at the top of a smooth fixed sphere. It is given a horizontal velocity v then:
Ait will start moving along a circular path if $v < \sqrt{g R}$
Bit will start moving along a circular path if $v > \sqrt{g R}$
Cit will start moving along a parabolic path if $v < \sqrt{g R}$
Dit will start moving along a parabolic path if $v > \sqrt{g R}$
Question 3 - Select One
If a particle of mass m start from along curved circular path shown in figure with constant tangential acceleration a, then net force at B on the particle has the magnitude :

Azero
B $2 m a \sqrt{1 + π^{2}}$
C $m a \sqrt{1 + π^{2}}$
D $m a π \sqrt{1 + π}$

RESONANCE-CIRCULAR MOTION-Exercise

Home
Ask Doubt
Profile