Find the mean, variance and standard deviation for the following data: 6,7,10,12,13,4,8,12
The correct Answer is:ar{x}=728=9
Variance =σ2=NΣx2−(Σx)2N2
Standard deviation, σ=√9.25
To find the mean, variance, and standard deviation for the given data: 6, 7, 10, 12, 13, 4, 8, and 12, we will follow these steps:
Step 1: Calculate the Mean
The mean (average) is calculated using the formula:
Mean(¯x)=1nn∑i=1xi
where n is the number of observations and xi are the data points.
1. Sum the data points:
6+7+10+12+13+4+8+12=72
2. Count the number of data points:
n=8
3. Calculate the mean:
¯x=728=9
Step 2: Calculate the Variance
Variance is calculated using the formula:
Variance(σ2)=1nn∑i=1(xi−¯x)2
1. Calculate each (xi−¯x)2:
- For x1=6: (6−9)2=(−3)2=9
- For x2=7: (7−9)2=(−2)2=4
- For x3=10: (10−9)2=(1)2=1
- For x4=12: (12−9)2=(3)2=9
- For x5=13: (13−9)2=(4)2=16
- For x6=4: (4−9)2=(−5)2=25
- For x7=8: (8−9)2=(−1)2=1
- For x8=12: (12−9)2=(3)2=9
2. Sum these squared differences:
9+4+1+9+16+25+1+9=74
3. Calculate the variance:
σ2=748=9.25
Step 3: Calculate the Standard Deviation
The standard deviation is the square root of the variance:
Standard Deviation(σ)=√σ2=√9.25≈3.04
Final Results
- Mean: 9
- Variance: 9.25
- Standard Deviation: 3.04
The mean (average) is calculated using the formula:
Mean(¯x)=1nn∑i=1xi
where n is the number of observations and xi are the data points.
6+7+10+12+13+4+8+12=72
n=8
¯x=728=9
Variance is calculated using the formula:
Variance(σ2)=1nn∑i=1(xi−¯x)2
- For x1=6: (6−9)2=(−3)2=9
- For x2=7: (7−9)2=(−2)2=4
- For x3=10: (10−9)2=(1)2=1
- For x4=12: (12−9)2=(3)2=9
- For x5=13: (13−9)2=(4)2=16
- For x6=4: (4−9)2=(−5)2=25
- For x7=8: (8−9)2=(−1)2=1
- For x8=12: (12−9)2=(3)2=9
9+4+1+9+16+25+1+9=74
σ2=748=9.25
The standard deviation is the square root of the variance:
Standard Deviation(σ)=√σ2=√9.25≈3.04
- Mean: 9
- Variance: 9.25
- Standard Deviation: 3.04
Topper's Solved these Questions
Similar Questions
Find the variance and standard deviation for the following data:
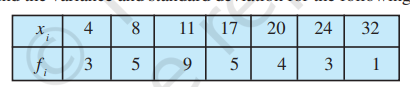
View SolutionFind the variance and standard deviation for the following data, 6, 7, 10, 12, 13, 4, 8, 12.
View SolutionFind the mean variance and standard deviation for the following data: 2,4,5,6,8,17
View SolutionFind the variance and standard deviation from the following data:

View SolutionFind the mean, variance and the standard deviation for the following data :
5,9,8,12,6,10,6,8
View SolutionFind the mean , mean deviation about the mean , variance and standard deviation for the following data
4,15,14,12,6,8,11
View SolutionFind the variance and standard deviation of the following data : 4,6,10,12,14,18,20
View SolutionFind the mean, variance and standard deviation for the following data:227,235,255,269,292,299,312,321,333,348
View SolutionFind the mean , mean deviation about the mean , variance and standard deviation for the following data

View SolutionFind the mean, variance and standard deviation for the numbers 4, 6, 10, 12, 7, 8, 13, 12.
View Solution
