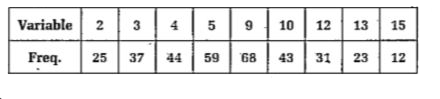
Calculate mean, variance and standard deviation of the following
frequency distribution:
Class Frequency
1−10 11
10−20 29
20−30 18
30−40 4
40−50 5
50−60 3
To calculate the mean, variance, and standard deviation of the given frequency distribution, we will follow these steps:
Step 1: Calculate the Midpoint (x_i) of Each Class
The midpoint (x_i) for each class is calculated as follows:
- For the class 1-10, midpoint = (1 + 10) / 2 = 5
- For the class 10-20, midpoint = (10 + 20) / 2 = 15
- For the class 20-30, midpoint = (20 + 30) / 2 = 25
- For the class 30-40, midpoint = (30 + 40) / 2 = 35
- For the class 40-50, midpoint = (40 + 50) / 2 = 45
- For the class 50-60, midpoint = (50 + 60) / 2 = 55
Step 2: Create a Table of Frequencies and Midpoints
| Class | Frequency (f_i) | Midpoint (x_i) | f_i * x_i |
|---------|------------------|----------------|-----------|
| 1-10 | 11 | 5 | 55 |
| 10-20 | 29 | 15 | 435 |
| 20-30 | 18 | 25 | 450 |
| 30-40 | 4 | 35 | 140 |
| 40-50 | 5 | 45 | 225 |
| 50-60 | 3 | 55 | 165 |
| Total | 70 | | 1470 |
Step 3: Calculate the Mean
The mean (μ) is calculated using the formula:
Mean=∑(fi⋅xi)∑fi
Substituting the values:
Mean=147070=21
Step 4: Calculate f_i * x_i^2
Now we need to calculate fi⋅x2i for each class:
| Class | Frequency (f_i) | Midpoint (x_i) | x_i^2 | f_i * x_i^2 |
|---------|------------------|----------------|-------|--------------|
| 1-10 | 11 | 5 | 25 | 275 |
| 10-20 | 29 | 15 | 225 | 6525 |
| 20-30 | 18 | 25 | 625 | 11250 |
| 30-40 | 4 | 35 | 1225 | 4900 |
| 40-50 | 5 | 45 | 2025 | 10125 |
| 50-60 | 3 | 55 | 3025 | 9075 |
| Total | 70 | | | 41,950 |
Step 5: Calculate the Variance
Variance (σ²) is calculated using the formula:
σ2=∑(fi⋅x2i)∑fi−(∑(fi⋅xi)∑fi)2
Substituting the values:
σ2=4195070−(21)2
Calculating:
σ2=599.2857−441=158.2857
Step 6: Calculate the Standard Deviation
Standard deviation (σ) is the square root of the variance:
σ=√158.2857≈12.58
Final Results
- Mean = 21
- Variance = 158.29 (approximately)
- Standard Deviation = 12.58 (approximately)
The midpoint (x_i) for each class is calculated as follows:
- For the class 1-10, midpoint = (1 + 10) / 2 = 5
- For the class 10-20, midpoint = (10 + 20) / 2 = 15
- For the class 20-30, midpoint = (20 + 30) / 2 = 25
- For the class 30-40, midpoint = (30 + 40) / 2 = 35
- For the class 40-50, midpoint = (40 + 50) / 2 = 45
- For the class 50-60, midpoint = (50 + 60) / 2 = 55
| Class | Frequency (f_i) | Midpoint (x_i) | f_i * x_i |
|---------|------------------|----------------|-----------|
| 1-10 | 11 | 5 | 55 |
| 10-20 | 29 | 15 | 435 |
| 20-30 | 18 | 25 | 450 |
| 30-40 | 4 | 35 | 140 |
| 40-50 | 5 | 45 | 225 |
| 50-60 | 3 | 55 | 165 |
| Total | 70 | | 1470 |
The mean (μ) is calculated using the formula:
Mean=∑(fi⋅xi)∑fi
Substituting the values:
Mean=147070=21
Now we need to calculate fi⋅x2i for each class:
| Class | Frequency (f_i) | Midpoint (x_i) | x_i^2 | f_i * x_i^2 |
|---------|------------------|----------------|-------|--------------|
| 1-10 | 11 | 5 | 25 | 275 |
| 10-20 | 29 | 15 | 225 | 6525 |
| 20-30 | 18 | 25 | 625 | 11250 |
| 30-40 | 4 | 35 | 1225 | 4900 |
| 40-50 | 5 | 45 | 2025 | 10125 |
| 50-60 | 3 | 55 | 3025 | 9075 |
| Total | 70 | | | 41,950 |
Variance (σ²) is calculated using the formula:
σ2=∑(fi⋅x2i)∑fi−(∑(fi⋅xi)∑fi)2
Substituting the values:
σ2=4195070−(21)2
Calculating:
σ2=599.2857−441=158.2857
Standard deviation (σ) is the square root of the variance:
σ=√158.2857≈12.58
- Mean = 21
- Variance = 158.29 (approximately)
- Standard Deviation = 12.58 (approximately)
Topper's Solved these Questions
Similar Questions
Knowledge Check
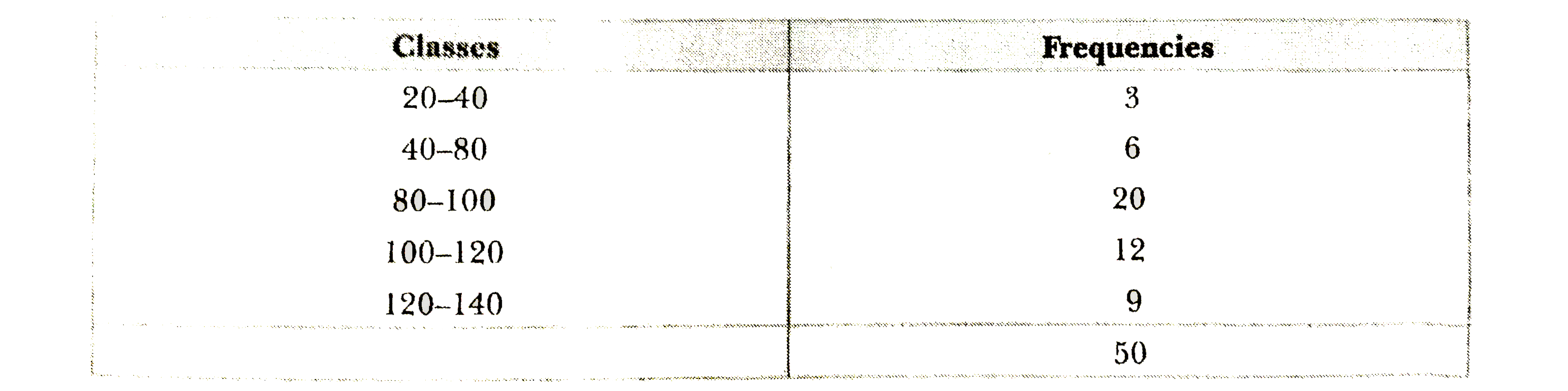
The standard deviation of the following frequency distribution
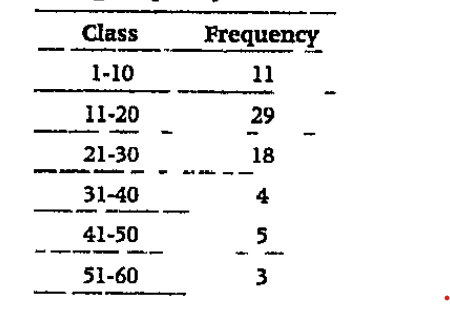 A12.7B13.6C15.3DNone of these
A12.7B13.6C15.3DNone of these
Calculate mean, Variance and Standard Deviation for the following distribution.

View SolutionFind the mean and variance for the following frequency distributions :

View SolutionFind the mean and variance for the following frequency distributions :

View SolutionFind the mean and variance for the following frequency distributions in
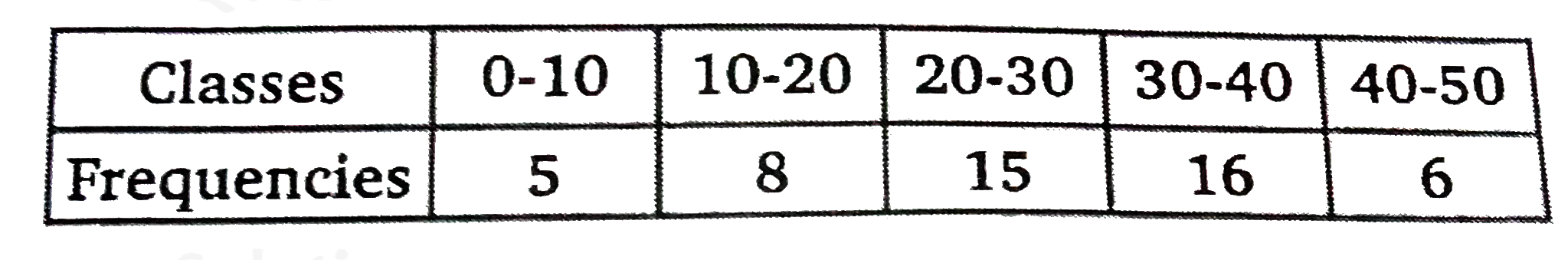
View SolutionFind the mean and variance for the following frequency distributions in
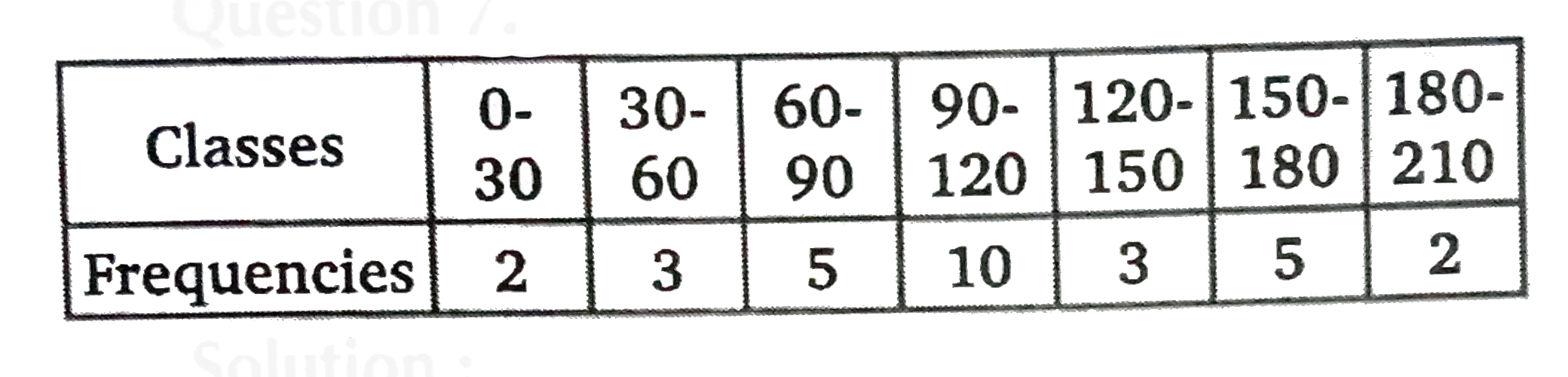
View SolutionCalculate mean, variance and standard deviation of the following frequency distribution:
Class Frequency
1−10 11
10−20 29
20−30 18
30−40 4
40−50 5
50−60 3
View SolutionCalculate the Mean Deviation about Mean and Standard Deviation for the following distribution:
View Solution