Find the mean and variance for the following frequency distributions :

Video Solution
Text Solution
Classes
Frequency
f_i
Mid point
x_i
fixi(xi−¯x)(xi−¯x)2fi(xi−¯x)2
0-30 2 15 30 -92 8464 16928
30-60 3 45 135 -62 3844 11532
60-90 5 75 375 -32 1024 5120
90-120 10 105 1050 2 4 40
120-150 3 135 405 28 784 2352
150-180 5 165 825 58 3364 16820
180-210 2 195 390 88 7744 15488<br>\sum{f_i} = N
= 30<br>\sum f_ix_i
= 3210<br>\sum f_i(x_i - \overline{x})^2
=68280<br>\overline{x} = \frac{1}{N}\sum_{i=1}^{n}f_ix_i = \frac{3210}{30} = 107<br>We know, Variance, \sigma^2 = \frac{1}{N}\sum_{i=1}^{n}(x_i - \overline{x})^2<br>\implies \sigma^2 = \frac{68280}{30} = 2276<br>Hence,Mean = 107 and Variance = 2276
|
Topper's Solved these Questions
Similar Questions
Find the mean for the following frequency distribution :
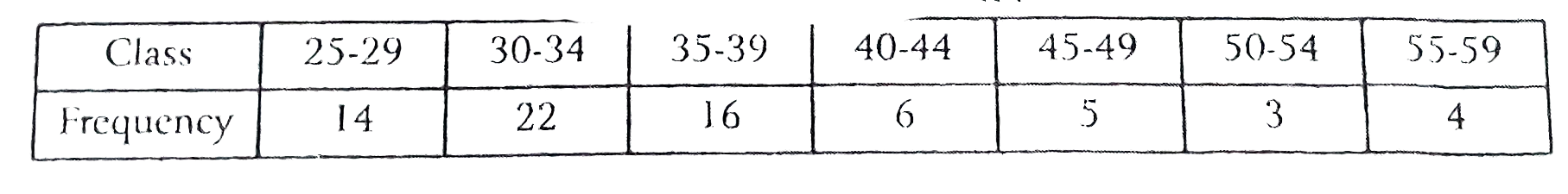
View SolutionFind the mean of the followings frequency distribution :

View SolutionFind the mean from the following frequency distribution:

View SolutionFind the mean and variance of the frequency distribution given below

View SolutionFind the mean of the following frequency distribution:

View SolutionFind the mean of the following frequency distribution:

View SolutionThe mean of the following frequency distribution is 50 :

View SolutionFind the missing frequency p for the following frequency distributions whose mean is 28.25.

View SolutionFind the mean marks from the following frequency distribution

View SolutionFind the value of p for the following frequency distribution whose mean is 16.6.

View Solution
