Calculate the mean and standard deviation of first n natural numbers.
The correct Answer is:Standard deviation, σ=√n2−112=12√n2−13
To calculate the mean and standard deviation of the first n natural numbers, we will follow these steps:
Step 1: Identify the first n natural numbers
The first n natural numbers are:
\( 1, 2, 3, \ldots, n \)
Step 2: Calculate the Mean
The mean (average) of a set of numbers is given by the formula:
\(
\text{Mean} ( \bar{x} ) = \frac{\text{Sum of all observations}}{\text{Number of observations}}
\)
For the first n natural numbers, the sum can be calculated using the formula for the sum of the first n natural numbers:
\(
\text{Sum} = \frac{n(n + 1)}{2}
\)
Thus, the mean can be calculated as:
\(
\bar{x} = \frac{\frac{n(n + 1)}{2}}{n} = \frac{n + 1}{2}
\)
Step 3: Calculate the Variance
The variance is defined as:
\(
\text{Variance} ( \sigma^2 ) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2
\)
This can be expanded to:
\(
\sigma^2 = \frac{1}{n} \left( \sum_{i=1}^{n} x_i^2 - n \bar{x}^2 \right)
\)
We need to find \( \sum_{i=1}^{n} x_i^2 \), which is given by the formula:
\(
\sum_{i=1}^{n} i^2 = \frac{n(n + 1)(2n + 1)}{6}
\)
Now substituting this into the variance formula:
\(
\sigma^2 = \frac{1}{n} \left( \frac{n(n + 1)(2n + 1)}{6} - n \left( \frac{n + 1}{2} \right)^2 \right)
\)
Calculating \( n \left( \frac{n + 1}{2} \right)^2 \):
\(
n \left( \frac{n + 1}{2} \right)^2 = n \cdot \frac{(n + 1)^2}{4} = \frac{n(n + 1)^2}{4}
\)
Substituting back into the variance formula:
\(
\sigma^2 = \frac{1}{n} \left( \frac{n(n + 1)(2n + 1)}{6} - \frac{n(n + 1)^2}{4} \right)
\)
Finding a common denominator (which is 12):
\(
\sigma^2 = \frac{1}{n} \left( \frac{2n(n + 1)(2n + 1)}{12} - \frac{3n(n + 1)^2}{12} \right)
\)
This simplifies to:
\(
\sigma^2 = \frac{1}{n} \cdot \frac{n(n + 1)}{12} \left( 2(2n + 1) - 3(n + 1) \right)
\)
Simplifying the expression inside the parentheses:
\(
2(2n + 1) - 3(n + 1) = 4n + 2 - 3n - 3 = n - 1
\)
Thus, we have:
\(
\sigma^2 = \frac{(n + 1)(n - 1)}{12}
\)
Step 4: Calculate the Standard Deviation
The standard deviation is the square root of the variance:
\(
\sigma = \sqrt{\sigma^2} = \sqrt{\frac{(n^2 - 1)}{12}}
\)
Final Results
- Mean of the first n natural numbers:
\(
\bar{x} = \frac{n + 1}{2}
\)
- Standard deviation of the first n natural numbers:
\(
\sigma = \sqrt{\frac{n^2 - 1}{12}}
\)
The first n natural numbers are:
\( 1, 2, 3, \ldots, n \)
The mean (average) of a set of numbers is given by the formula:
\(
\text{Mean} ( \bar{x} ) = \frac{\text{Sum of all observations}}{\text{Number of observations}}
\)
For the first n natural numbers, the sum can be calculated using the formula for the sum of the first n natural numbers:
\(
\text{Sum} = \frac{n(n + 1)}{2}
\)
Thus, the mean can be calculated as:
\(
\bar{x} = \frac{\frac{n(n + 1)}{2}}{n} = \frac{n + 1}{2}
\)
The variance is defined as:
\(
\text{Variance} ( \sigma^2 ) = \frac{1}{n} \sum_{i=1}^{n} (x_i - \bar{x})^2
\)
This can be expanded to:
\(
\sigma^2 = \frac{1}{n} \left( \sum_{i=1}^{n} x_i^2 - n \bar{x}^2 \right)
\)
We need to find \( \sum_{i=1}^{n} x_i^2 \), which is given by the formula:
\(
\sum_{i=1}^{n} i^2 = \frac{n(n + 1)(2n + 1)}{6}
\)
Now substituting this into the variance formula:
\(
\sigma^2 = \frac{1}{n} \left( \frac{n(n + 1)(2n + 1)}{6} - n \left( \frac{n + 1}{2} \right)^2 \right)
\)
Calculating \( n \left( \frac{n + 1}{2} \right)^2 \):
\(
n \left( \frac{n + 1}{2} \right)^2 = n \cdot \frac{(n + 1)^2}{4} = \frac{n(n + 1)^2}{4}
\)
Substituting back into the variance formula:
\(
\sigma^2 = \frac{1}{n} \left( \frac{n(n + 1)(2n + 1)}{6} - \frac{n(n + 1)^2}{4} \right)
\)
Finding a common denominator (which is 12):
\(
\sigma^2 = \frac{1}{n} \left( \frac{2n(n + 1)(2n + 1)}{12} - \frac{3n(n + 1)^2}{12} \right)
\)
This simplifies to:
\(
\sigma^2 = \frac{1}{n} \cdot \frac{n(n + 1)}{12} \left( 2(2n + 1) - 3(n + 1) \right)
\)
Simplifying the expression inside the parentheses:
\(
2(2n + 1) - 3(n + 1) = 4n + 2 - 3n - 3 = n - 1
\)
Thus, we have:
\(
\sigma^2 = \frac{(n + 1)(n - 1)}{12}
\)
The standard deviation is the square root of the variance:
\(
\sigma = \sqrt{\sigma^2} = \sqrt{\frac{(n^2 - 1)}{12}}
\)
- Mean of the first n natural numbers:
\(
\bar{x} = \frac{n + 1}{2}
\)
- Standard deviation of the first n natural numbers:
\(
\sigma = \sqrt{\frac{n^2 - 1}{12}}
\)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Standard deviation of first n odd natural numbers is
A√nB√(n+2)(n+1)3C√n2−13DnThe standard deviation for first natural number is
A5.5B3.87C2.97D2.87The standard deviation of the first n natural numbers is
A√n2+112Bn2−112C√n2−112Dn2+112
Find the mean, variance and standard deviation of first n natural numbers.
View SolutionFind the mean, standard deviation and variance of first n natural numbers.
View SolutionFind the Standard Deviation of First 10 Even Natural numbers.
View SolutionCalculate mean and standard deviation from the following data:
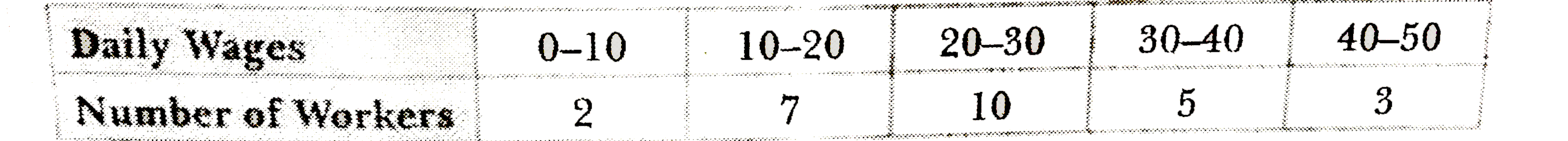
View SolutionFind the standard deviation of the first n natural numbers.
View Solution

