In the shown figure, there are two long fixed parallel conducting rails (having negligible resistance) and are separated by distance L.A uniform rod of resistance R and mass M is placed at rest on frictionless rails. Now at time t = 0, a capacitor having charge Q0 and capacitance C is connected across rails at ends a and b such that current in rod(cd) is from c towards d and the rod is released. A uniform and constant magnetic field having magnitude B exists normal to plane of paper as shown. (Neglect acceleration due to gravity)

When the acceleration of rod is zero, the speed of rod is :
Q0R2BCM+B2L2C2
Q0LBM+B2L2C
Q0LBM+B2L4C4
Q0LBM+B2L2C2
The correct Answer is:B
At any instant t, the charge on capacitor q velocity of rod v and the current I through rod are as shown
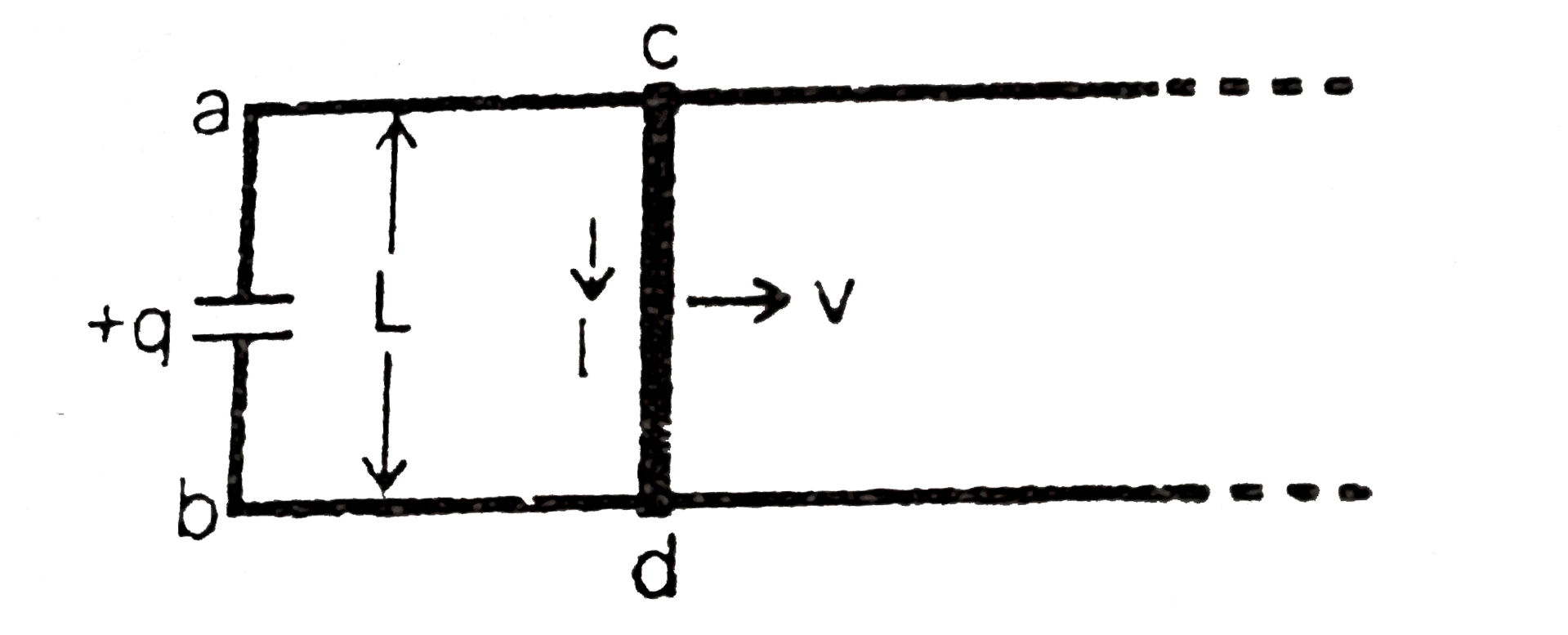
∴mdvdt=BIL=B(−dqdt)L......(1)
⇒v∫0mdv=−q∫Q0BLdq
solving we get
q=Q0−MvBL....(2)
Also qC=BLV+IR=BLv−Rdqdt......(3)
from equation (1) and (3)
qC=BLv+mRBLdvdt....(4)
from (4) when dvdt=0
⇒qC=BLv....(5)
From (2) and (5). At instant acceleration is zero
V=Q0LBM+B2L2Candq=B2L2CQ0M+B2L2C.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.55
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.56
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.53
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Shows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
View SolutionA pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table. A mass m tied to the other end of the string hangs vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate

a. the terminal velocity achieved by the rod and
b. The acceleration of the mass of the instant when the velocity of the rod is half the terminal velocity.
View Solution
Knowledge Check
In the shown figure, there are two long fixed parallel conducting rails (having negligible resistance) and are separated by distance L. A uniform rod of resistance R and mass M is placed at rest on frictionless rails. Now at time t=0, a capacitor having charge Q0 and capacitance C is connected across rails at ends a and b such that current in rod (cd) is from c towards d and the rod is released. A uniform and constant magnetic field having magnitude B exists normal to plane of paper as shown. (Neglect acceleration due to gravity)
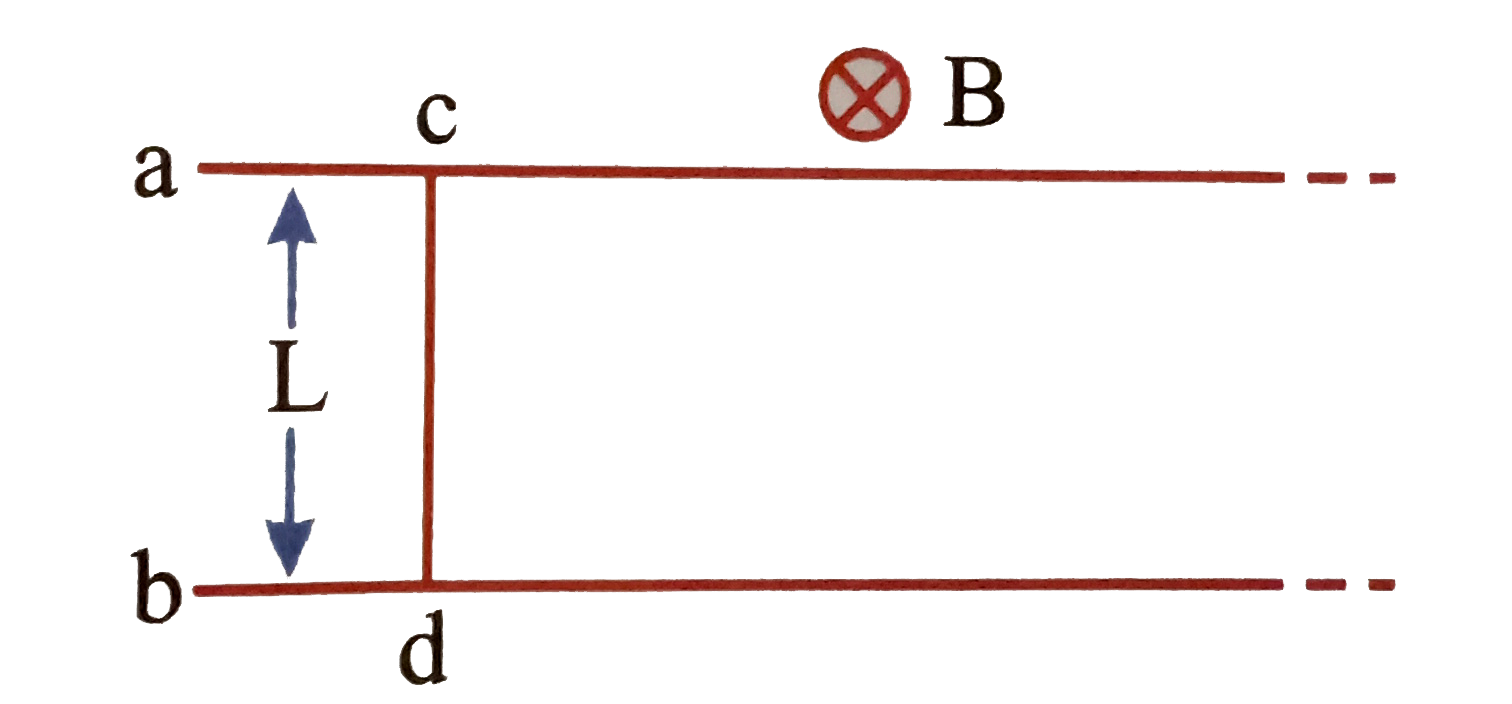
When the acceleration of rod is zero, the charge on capacitor is:AB2L2CQ0M+B2L2CBB2R4C3Q0M+B2L2C2CB2R4C3Q0M+B2R4C4DB2L2CQ0M+B2L2C2In the shown figure, there are two long fixed parallel conducting rails (having negligible resistance) and are separated by distance L. A uniform rod of resistance R and mass M is placed at rest on frictionless rails. Now at time t=0, a capacitor having charge Q0 and capacitance C is connected across rails at ends a and b such that current in rod (cd) is from c towards d and the rod is released. A uniform and constant magnetic field having magnitude B exists normal to plane of paper as shown. (Neglect acceleration due to gravity)
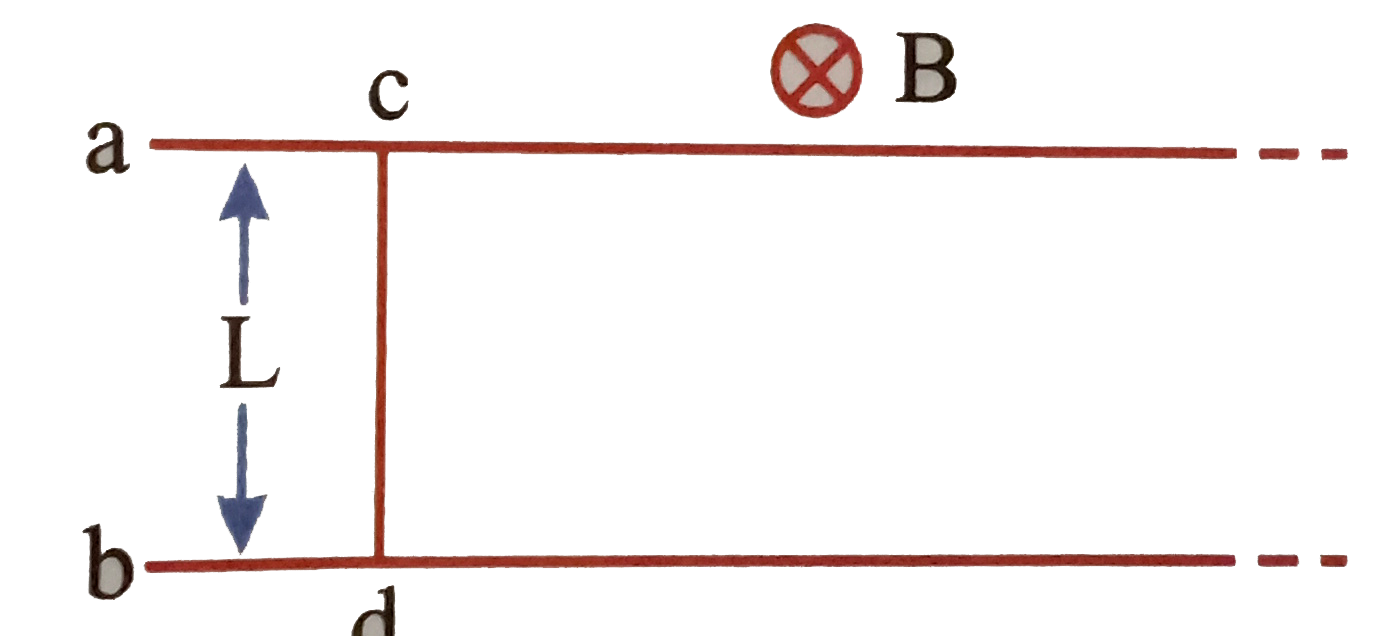
When the speed of rod is v, the charge on capacitor is :A(Q0−RMLBCv)B(Q0−MRC2Bv)C(Q0−MLBv)D(Q0−MRCBv)Two vertical conducting rails separted by distance 1.0m are placed parallel to z-axis as shown in figure. At z=0, a capacitor of 0.15F is connected between the rails and a metal rod of mass 100g placed across the rails slides down along the rails. if a constant magnetic fields of 2.0 T exists perpendicular to the plane of the rails, what is the acceleration of the rod?
 A2.5m/s2BzeroC9.8m/s2)D1.4m/s2)
A2.5m/s2BzeroC9.8m/s2)D1.4m/s2)
A pair of parallel horizontal conducting rails of negligible resistance shorted at one end is fixed on a table. The distance between the rails is L. A conducting massless rod of resistance R can slide on the rails frictionlessly. The rod is tied to a massless string which passes over a pulley fixed to the edge of the table, A mass m, tied to the other end of the string hanges vertically. A constant magnetic field B exists perpendicular to the table. If the system is released from rest, calculate.
(i) the terminal velocity achieved by the rod, and
the acceleration of the mass at the instant when the velocity of the rod is half the terminal velocity.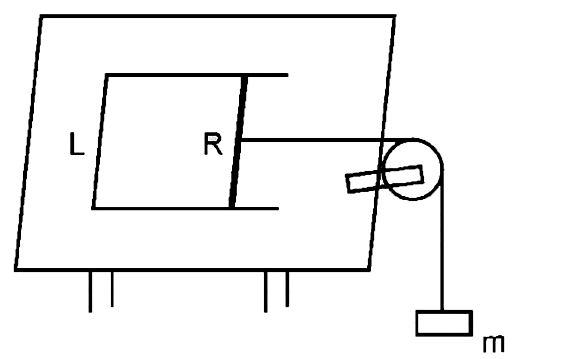
View SolutionAs shown in figure, the two parallel conducting rails, in a horizontal plane, are connected at one end by an inductor of inductance L. A slider (metallic) of mass m, is imparted a Velocity v0, upon the rails, as shown in figure. The period of oscillation of the conducting rod is
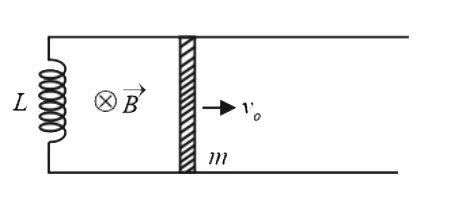
View SolutionA pair of long, smooth, parallel, horizontal, conducting rails are joined to a cell at one end. There are no external electric or magnetic fields. A metal rod is placed on the rails. The rod will
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
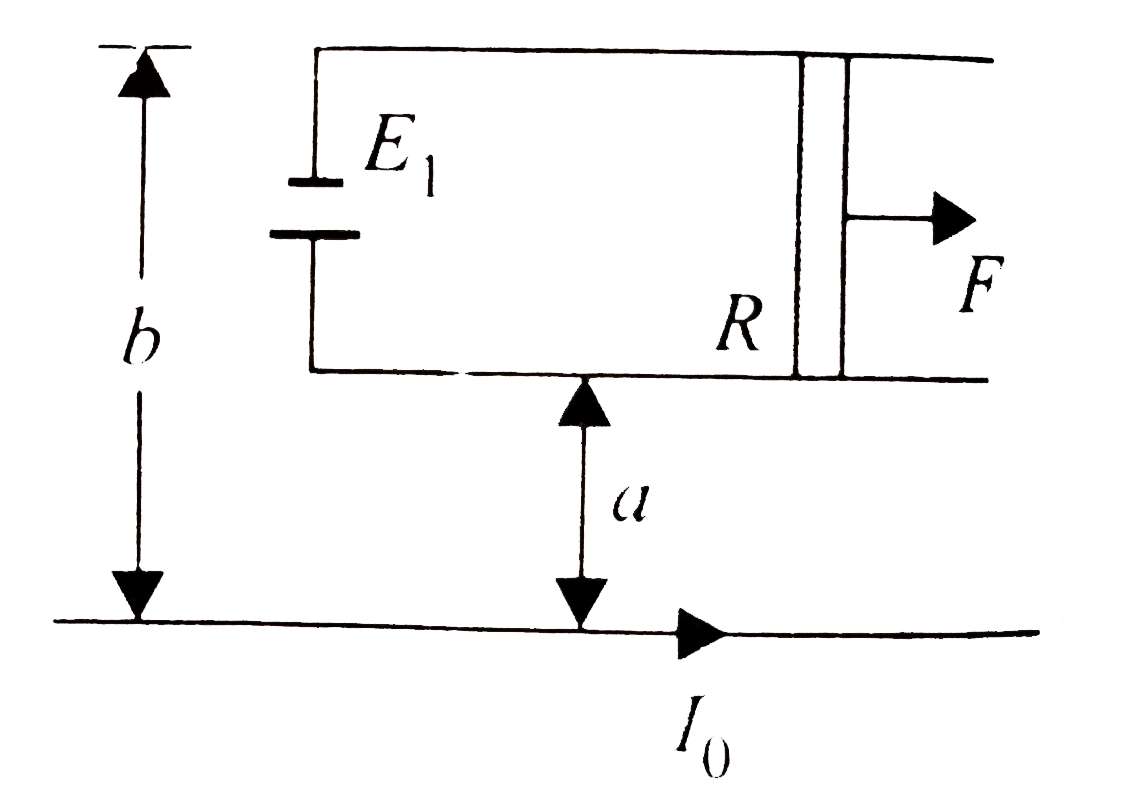
Find the value of current in the circuit if the rod slides with constant velocity v0
View SolutionA metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
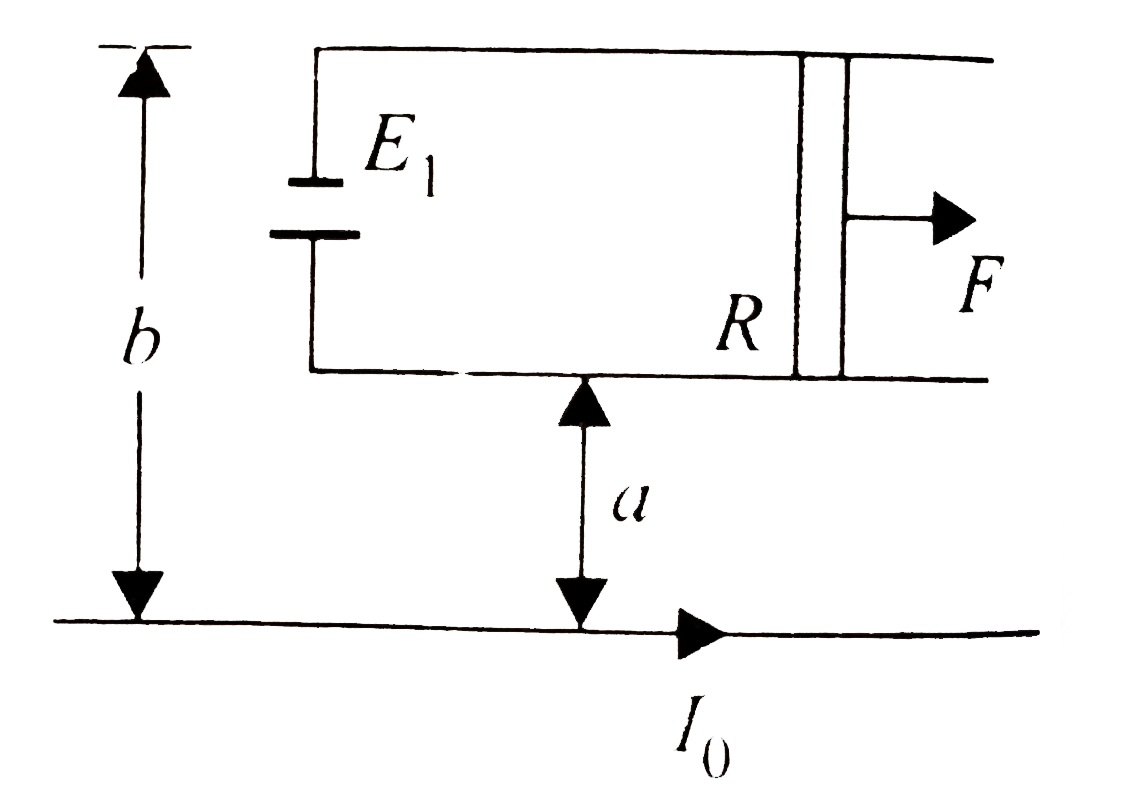
Find the value of F if the rod slides with constant velocity
View Solution