A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current . The distance of the rails from the wire are b and a respectively.
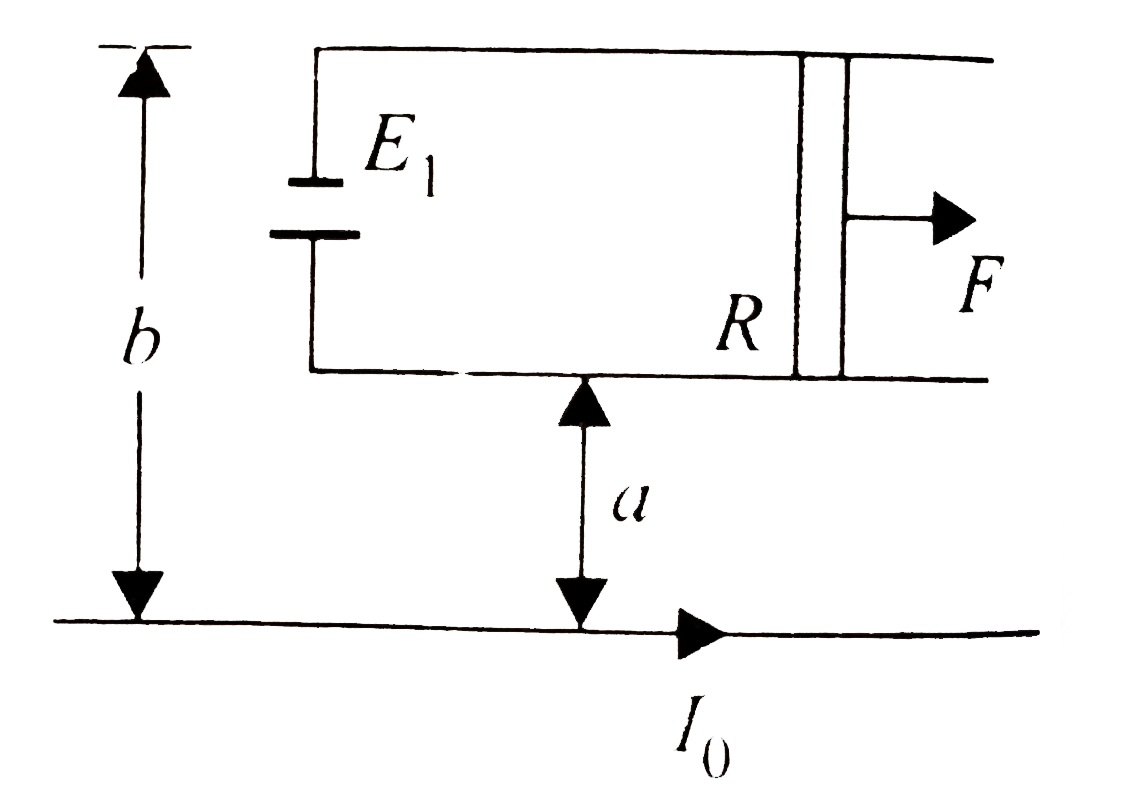
Find the value of F if the rod slides with constant velocity
None of these
The correct Answer is:C
(a) Magnetic flux linked with the differential area element shown in fig.
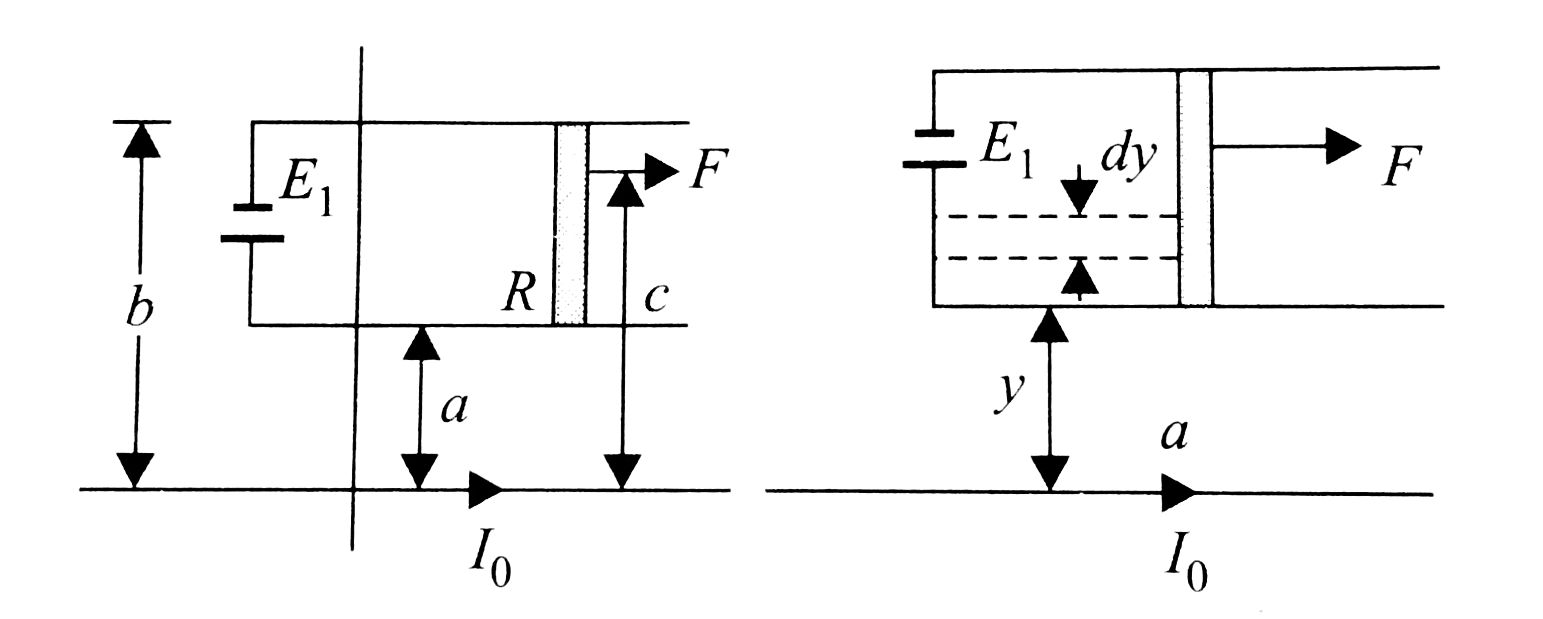
Net flux =
emf can be calculated using motional emf method, emf developed due to motion of the conductor has an opposite secse to the emf of the cell
therefore,
(b)
.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Integer
Explore 12 Videos
- MISCELLANEOUS VOLUME 5Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 5Exercise:Multiple Correct
Explore 34 Videos
- MISCELLANEOUS VOLUME 3Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 3Exercise:True and False
Explore 3 Videos
- Moving charges and magnetismBook:CENGAGE PHYSICSChapter:Moving charges and magnetismExercise:Question Bank
Explore 20 Videos
Similar Questions
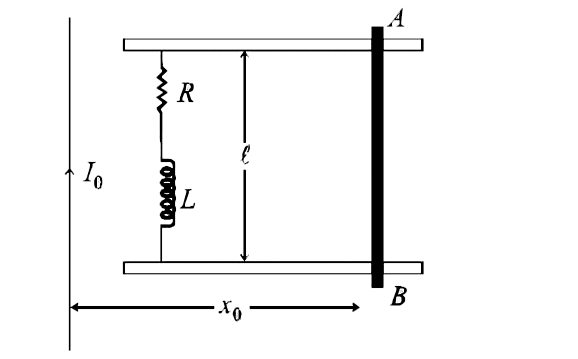
A metal bar AB can slide on two parallel thick metallic rails separated by a distance l. A resistance R and an inductance L are connected to the rails as shown in the figure. A long straight wire carrying a constant current I0 is placed in the plane of the rails and perpendicular to them as shown. The bar AB is held at rest at a distance x0 from the long wire. At t=0, it is made to slide on the rails away from wire. Answer the following questions.
(a) Find a relation among i,didtanddϕdt, where i is the current in the circuit and ϕ is the flux of the megnetic field due to the long wire through the circuit.
(b) It is observed that at time t=T, the metal bar AB si at a distance of 2x0 from the long wire and the resistance R carries a current (i1). Obtain an expression for the net charge that has flown through riesistance R form t=0 to t=T.
(c) THe bar is suddenly stopped at time T. THe current through resistance R is found to be i14 at time 2T. Find the value of LR in terms of hte other given quantities.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View Solution
Knowledge Check
A metallic rod of mass m and resistance R is sliding over the 2 conducting frictionless rails as shown in Fig. An infinitely long wire carries a current I0. The distance of the rails from the wire are b and a respectively.
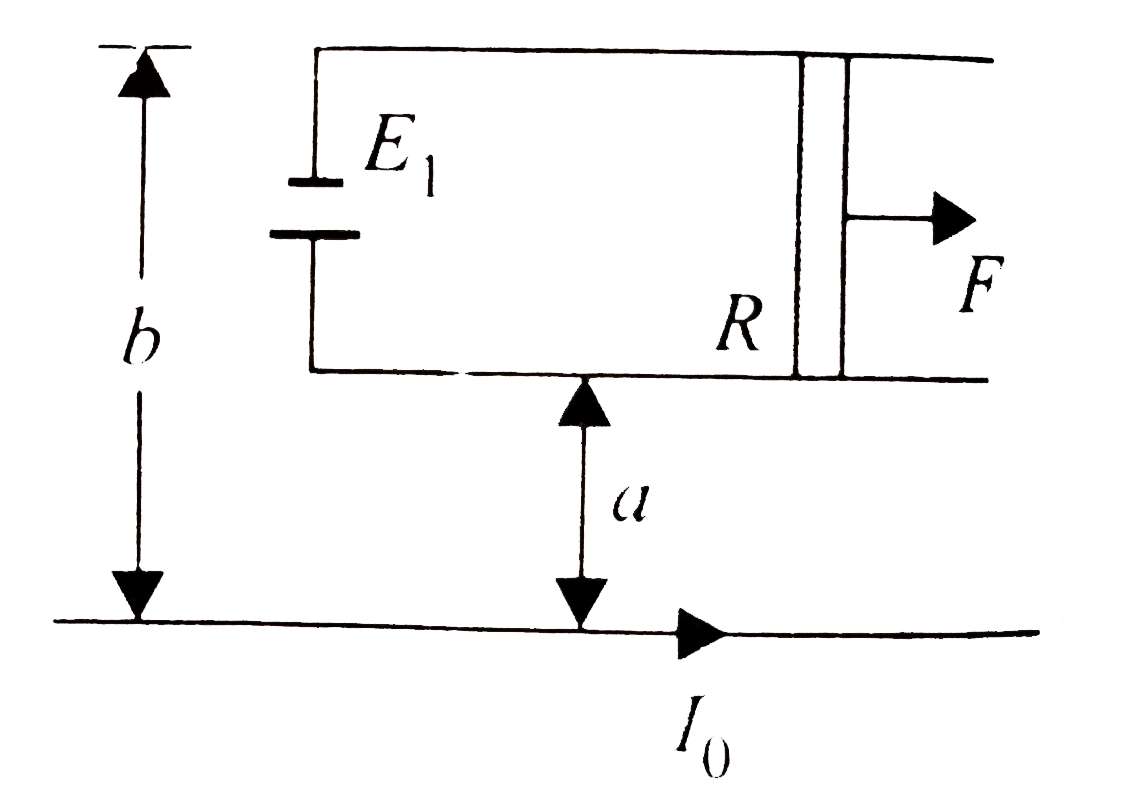
Find the value of current in the circuit if the rod slides with constant velocity v0A1R{E−μ0I0v02π1n∣∣∣ba∣∣∣}B1R{E+μ0I0v02π1n∣∣∣ba∣∣∣}C1R{E−μ0I0v0π1n∣∣∣ba∣∣∣}DNone of theseThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
A|B|=(μ04π)2irB|B|=(μ04π)r2iC|B|=(4πμ0)2irD|B|=(4πμ0)r2iA metal bar AB can slide without friction on two parallel thick metallic rails separated by a distance I. A resistance R and an inductance L are connected to the rails as shown in the figure. An infinite long straight wire carrying a constant current I0 is placed on the plane of the rails as shown. The bar AB is held at rest at a distance x0 from the long wire. At t = 0, it is made to slide on the rails away from the wire.
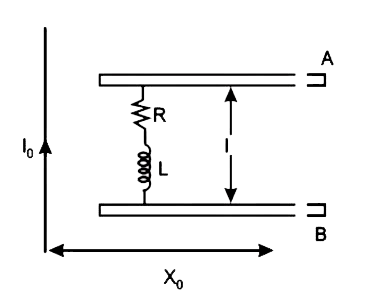
It is observed that at time t = T, the metal bar AB is at a distance of 2x0 from the long wire and the resistance R carries a current ix. Obtain an expression for the net charge that has flown through resistance R from t = 0 to t = T.A1R[μ0I2πln(2)−Li1]B1R[l2πI0ln(2)−Li1]C1R[μ0I0l2πln(2)−Li1]D1R[μ0I02πln(2)−Li1]
A constant current i flows through a metal rod of length L and mass m that slides on frictionless rails as shown in Fig. If the initial speed of the rod is v0 towards right and a magnetic field B acts vertically up, find (a) the speed of the rod as a function of time, (b) the total distance moved by the rod before coming to a stop.

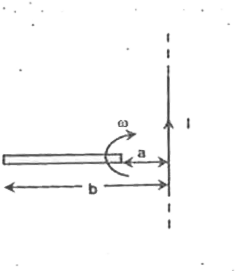
View SolutionA copper rod moves with a constant angular velocity ω about a long straight wire carrying a current I. If the ends of the rod from the wire are at distances a and b, then the e.m.f induced in the rod is
View SolutionIn the figure shown AB is a plastic rod moving with a constant velocity v, W is an infinite long wire carrying current I. The end of the rod which is at higher potential is

View SolutionA conducting rod of mass m and length l is free to move without friction on two parallel long conducting rails, as shown below. There is a resistance R across the rails. In the entire space around, there is a uniform magnetic field B normal to the plane of the rod and rails. The rod is given an impulsive velocity v0-

Finally, the initial energy 12mv20
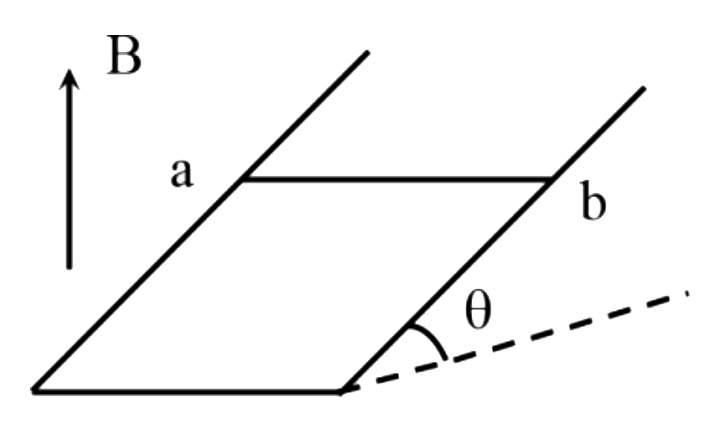
View SolutionA wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
View Solution