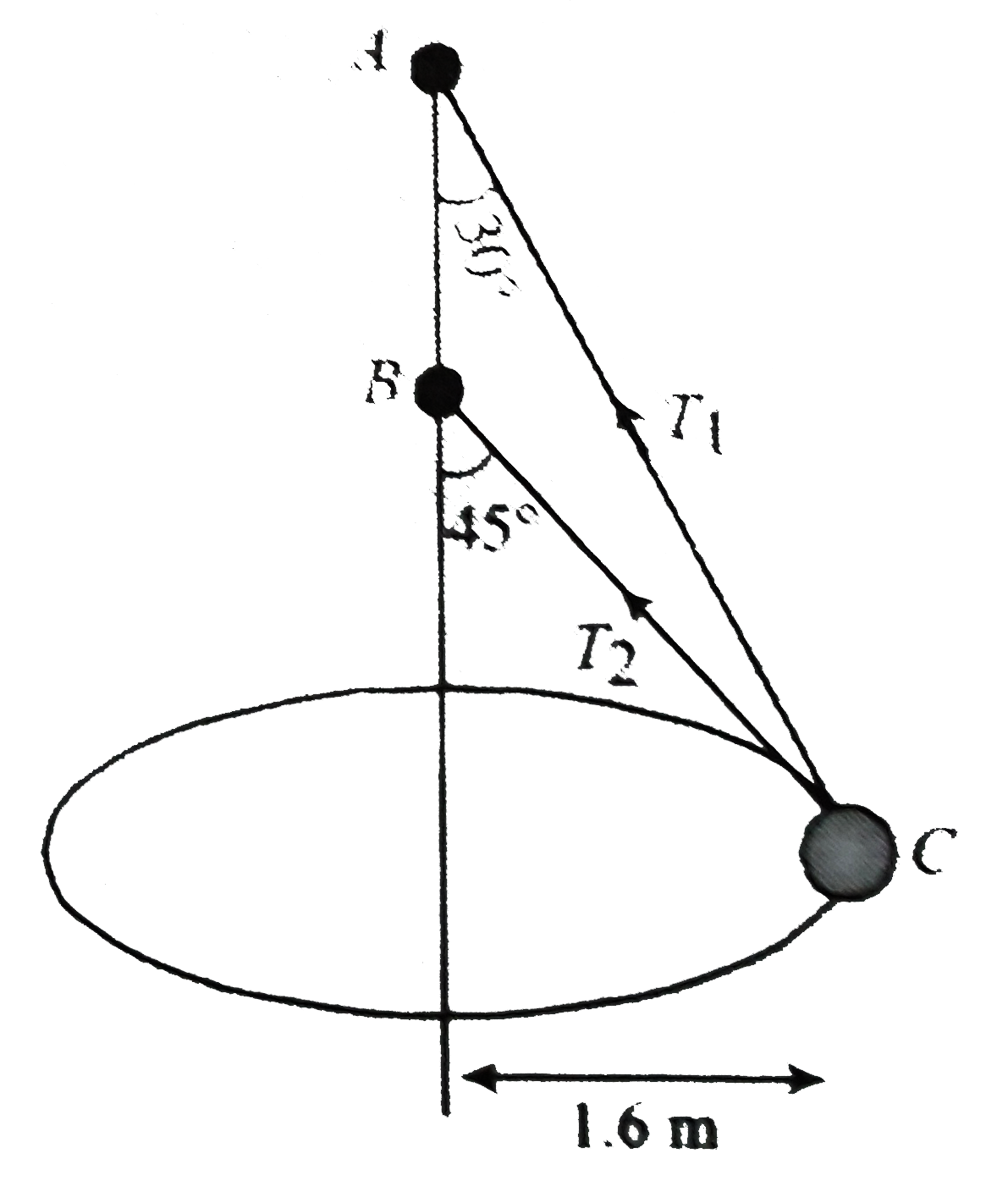
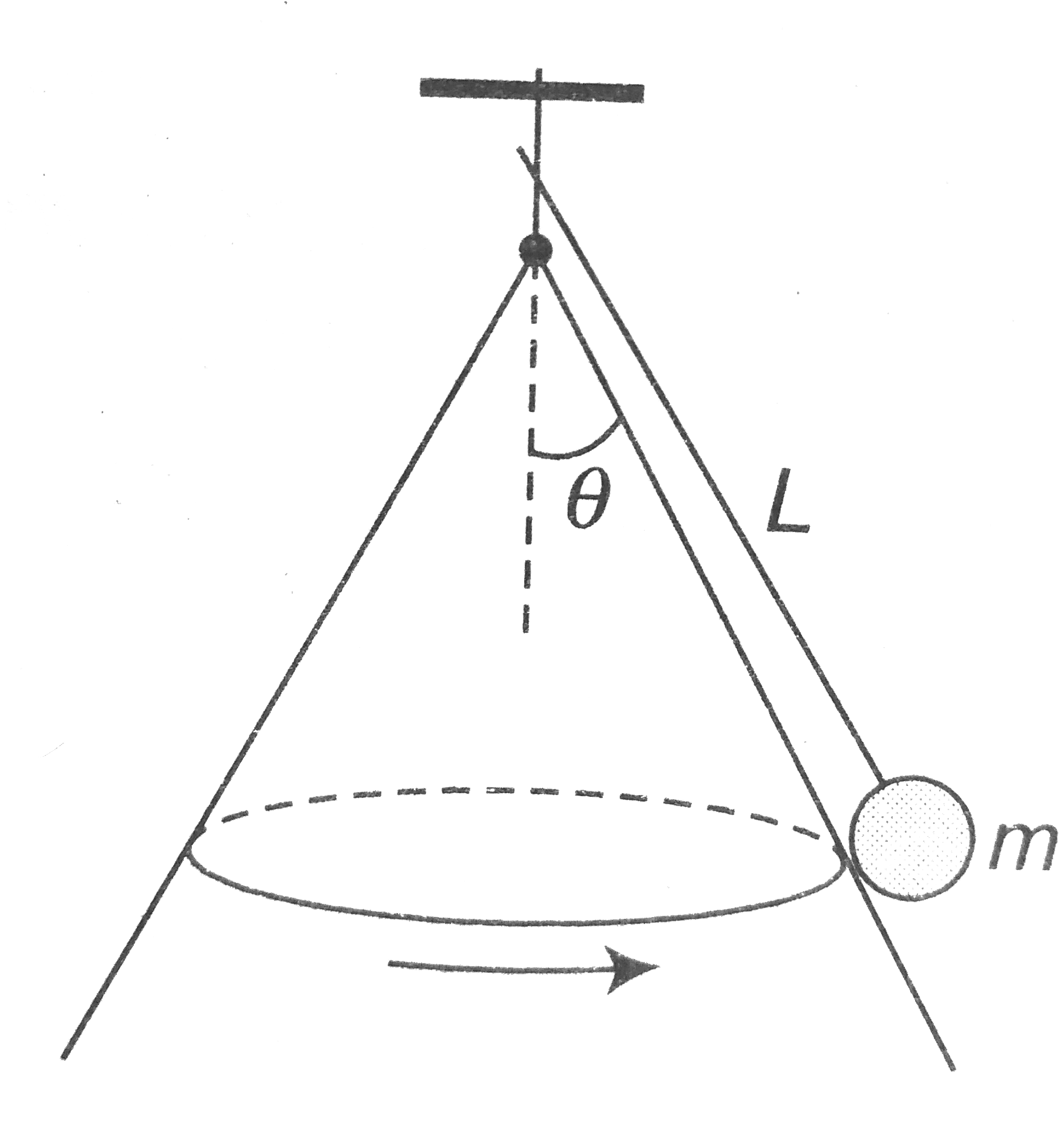
A small sized mass m is attached by a massless string (of length L) to the top of a fixed frictionless solid cone whose axis is vertical. The half angle at the vertex of cone is theta. If the mass m moves around in a horizontal circle at speed v , what is the maximum value of v for which mass stay in contact with the comes? (g is acceleration due to gravity.)
√gLcosθ
√gLsinθ
√gLsinθtanθ
√gLtanθ
The correct Answer is:C
At maximum velocity the mass will just loose contact with cone and will behave like free conical pendulum with time period :
T=2π√Lcosθg⇒ω=2πT√gLcosθ
Hence vmax=(Lsinθ)ω=√gLsinθtanθ.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.52
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.53
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.50
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Knowledge Check
A paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are
 AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronly
AmgandTBmg,T,mv2rdirected in wardsCmg,T,mv2rdirected outewardsDmv2ronlyA bob of mas M is suspended by a massless string of length L. The horizontal velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies.
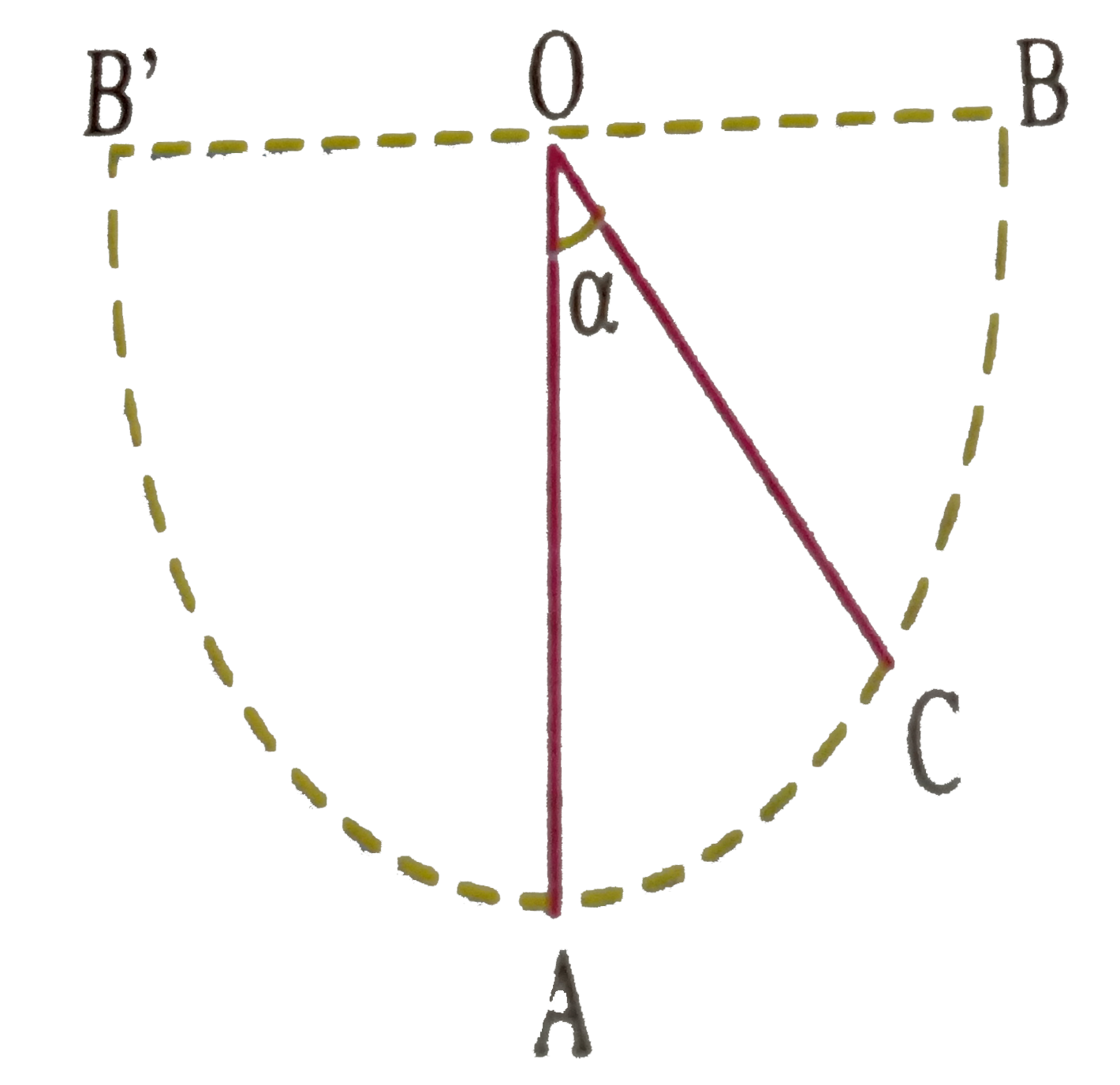 .Aθ=π4Bπ4<θ<π2Cπ2<θ<3π4D3π4<θ<π
.Aθ=π4Bπ4<θ<π2Cπ2<θ<3π4D3π4<θ<πA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
Amove towards the centreBmove away from the centreCmove along a tangentDstop
A small ball of mass m is attached to a string of lengh R and moves in a vertical circle with a speed v m/s about a fixed point O as illustrated in fig. Find the tension in the string, when it makes an angle θ with the vertical, in terms of v,θ and g.
View SolutionA stone of mass 5 kg is tied to a string of length 10 m is whirled round in a horizontal circle. What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N?
View SolutionA bead of mass m is attached to the mid-point of a taut, weightless string of length l and placed on a frictionless horizontal table.
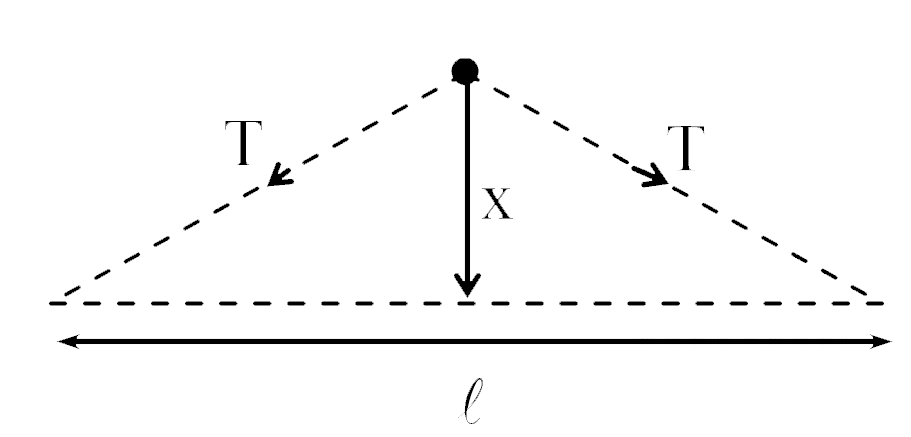
Under a small transverse displacement x, as shown, if the tension in the string is T, then the frequency of oscillation is-
View SolutionA particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
View SolutionA particle of mass 'm' is moving in horizontal circle inside a smooth inverted fixed vertical cone above height 'h' from apex. Angle of cone is θ, then
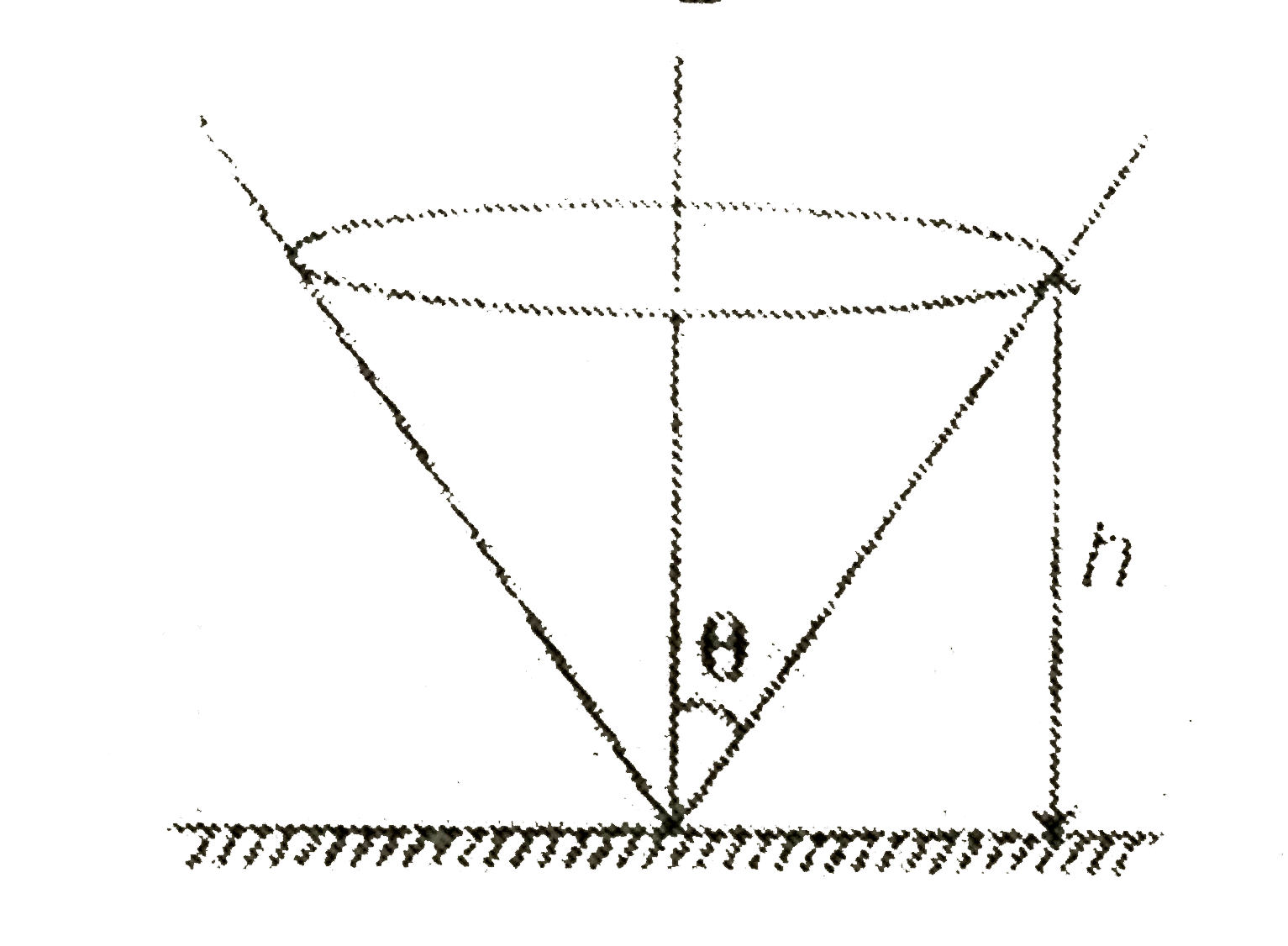
View Solution