Direction :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
A small sphere of mass 2.00 g is released from rest in a large vessel filled with oil. The sphere approaches a terminal speed of 10.00 cm/s. Time required to achieve speed 6.32 cm/s from start of the motion is (Take g=10.00m/s2) :
5.00×10−3s
1.00×10−2s
2.5×10−3s
1.00×10−3s
The correct Answer is:B
Using Vτ=mgb⇒mb=10−2s
In this time sphere would achieve 0.63 fraction of its terminal speed 10 cm/s
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.52
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.53
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.50
Explore 9 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Three point masses A,B,C each of mass m are moving on the same circular path and are always equidistant from each other. The radius of circular is R and the speed of each mass is same and equal to V. The only force acting on each mass is the graviational force because of the other two masses. Choose the correct statement
View SolutionAn AC voltage source V=V0siωtis connected across resistance R and capacitance C as shown in figureure. It is given that R=1ωC. The peak current is I0. If the angular frequency of the voltage source is changed to ω√3, then the new peak current in the circuit is
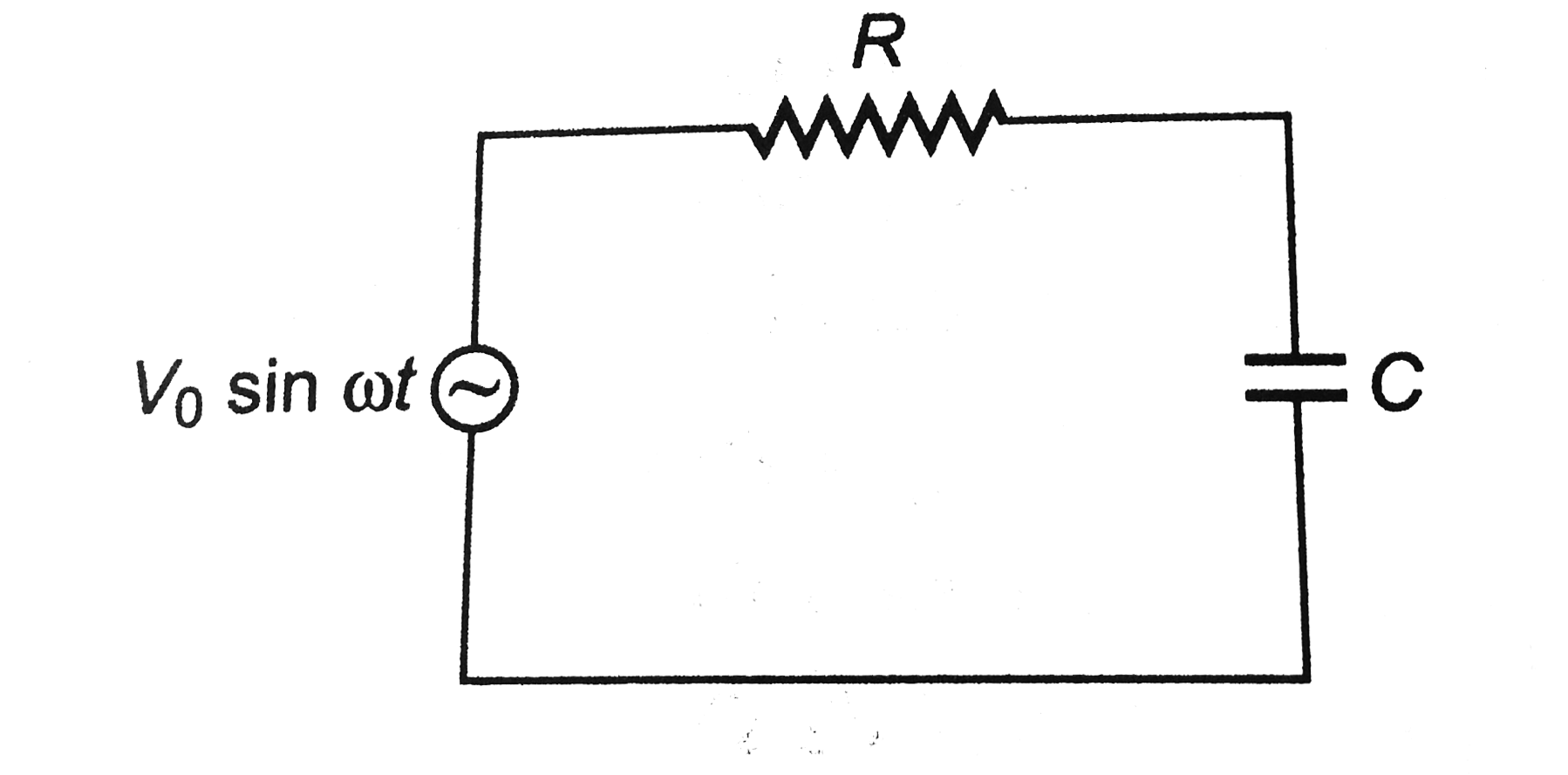 .
.
View SolutionFrom a cylinder of radius R, a cylider of radius R/2 is removed, as shown in Fig. Current flowing in the remaining cylinder is I. Then, magnetic field strength is
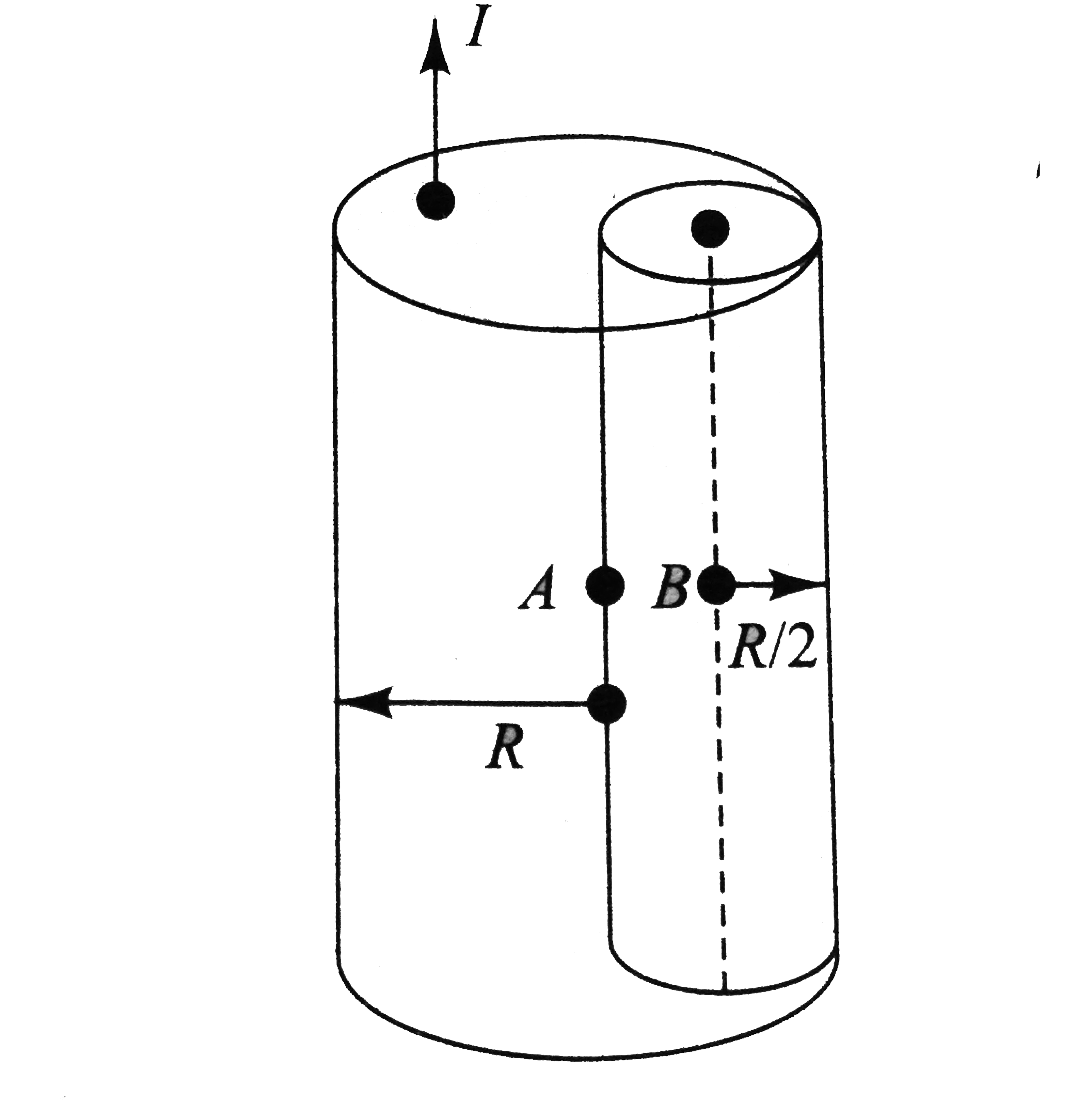
View SolutionA galvanometer having 30 divisions has a current sensitivity of 20μA/division. It has a resistance of 25Ω. How will you convert it into an ammeter upto 1 ampere? How will you convert this ammeter into a voltmeter up to 1 volt?
View SolutionAn electromagnetic wave of frequency v=3.0MHz passes from vacuum into a dielectric medium with permittivity ε=4.0. Then
View SolutionDirection : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} Which object has greatest terminal speed in the liquid ?
View SolutionDirection : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends on the properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} Which object would first acquire half of their respective terminal speed in minimum time from start of the motion of all were released simultaneously ?
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If an object of mass 2 kg and constant b=4N−sm has terminal speed vT in a liquid then time required to reach 0.63vT from start of the motion is :
View SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
At the start of motion when object is released in the liquid, its acceleration is :
View SolutionDirection : Resistive force proportional to object velocity At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as R = -bv Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity. Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here. Thus mg - bv = m (dv)/(dt) rArr (dv)/(dt) = g - (b)/(m) v Solving the equation v = (mg)/(b) (1- e^(-bt//m)) where e=2.71 is the base of the natural logarithm The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v_(1) and then on it continues to move with zero acceleration mg - b_(T) =0 rArr m_(T) = (mg)/(b) Hence v = v_(T) (1-e^((vt)/(m))) In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table. {:("Object",I,II,II,IV),("Mass (in kg.)",1,2,3,4),(underset("in (N-s)/m")("Constant b"),3.7,1.4,1.4,2.8):} If buoyant force were also taken into account then value of terminal speed would have
View SolutionAn object is moving though air at a speed v. If the area of the object normal to the direction of velocity is A and assuming elastic collision with air molecules, then the resistive force on the object is propotional to-(assume that molecules striking the object were initially at rest)
View SolutionAn object is moving through the liquid. The viscous damping force acting on it is proportional to the velocity. Then dimensions of constant of proportionality are
View Solutionवायु में गतिमान किसी वस्तु पर वायु का घर्षण बल वस्तु के वेग के अनुक्रमानुपाती होता है , अनुक्रमानुपाती नियतांक (b) की विमायें क्या होंगी ?
View SolutionAn object is moving in a fluid. The force of the viscous force on it is proportional to the velocity, then the dimension of the proportional constant will be
View SolutionAn object is moving through the liquid. The viscous damping force acting on it is proportional to the velocity. Then dimensions of constant of proportionality are
View Solution

