A small ball of mass m is attached to a string of lengh R and moves in a vertical circle with a speed v m/s about a fixed point O as illustrated in fig. Find the tension in the string, when it makes an angle θ with the vertical, in terms of v,θ and g.
1. The speed of the ball is not uniform in this example as the gravitational force has a tangential component, at almost all points on the path.
2. It is not a uniform circular motion.
Calculations : Making the free body diagram, we see that the only forces acting on the ball are the weight and the tension exerted by the cord. Tension is always acting radialy inward. We need to resolve mg into a tangential component mgsinθ and a radiual component mgcosθ.
Apply Newton.s second law to the ball in the tangential direction,
mgsinθ=mat
at=gsinθ
Apply Newton.s second law to the forces acting on the ball in the radial direction.
T−mgcosθ=mv2R
t=mg(v2Rg+cosθ)
Learn: It is importat to note that v in the expressio above varies for different positions as there is net tangential force acting on the particle.
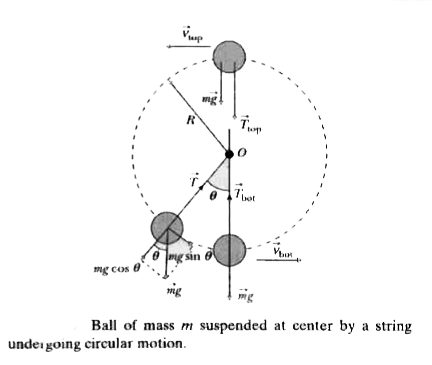
Case 1: What speed would the ball have at the top of the circle if the tension in the cord becomes zero at this point?
Keeping tension equal to zero in the abvoe expression, we get
0=mg(v2topRg−1)⇒vtop=√gR
Case 2: What if the ball is given an initial velocity such that the speed at the top is less than this value? In this case the ball will not reach the top of the circle, as the tension in the string becomes zero to some lower point. The ball becomes a projectile as only force acting is gravity and ball has some oblique velocity.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PROBLEMS
56 Videos
- CIRCULAR MOTIONBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCULAR MOTIONEXERCISE - PRACTICE QUESTIONS(SINGLE CORRECT CHOICE TYPE)
40 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
- CURRENT AND RESISTANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
A small body of mass m is tried to a string and revolved in a vertical circle of radius r. If the tension in the string at the highest point is mg, what is its speed there?
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution
Knowledge Check
A body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
Amu2lBmu2l+mgcosθCmu2l+mg(2cosθ−3)Dmu2l+mg(3cosθ−2)A stone of mass m is tied to a string and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
Am[g+4π2r]Bm[g+π2n2r260]Cm[g+π2n2r900]Dm[g+n2r2]A mass of 5 kg is tied to a string of length 1.0 m and is rotated in vertical circle with a uniform speed of 4m/s . The tension in the string will be 130 N when the mass is at (g= 10m/s2)
Ahighest pointBmid wayCbottomDcannot be justified
A mass of 5 kg is tied to a string of length 1.0 m is rotated in vertical circle with a uniform speed of 4m/s . The tension in the string will be 170 N when the mass is at (g=10m/s2)
View SolutionA stone of mass m is tied to a strin and is moved in a vertical circle of radius r making n revolution per minute. The total tension in the string when the stone is its lowest point is.
View SolutionA point mass of 2 kg tied to a string of 1 m length is rotated in a vertical circle with uniform speed of 4m/s. The tension in the string is nearly 32 N when mass is at
View SolutionA mass of 2 kg tied to a string 1 m length is rotate in a verticle circle with a uniform speed of 4m/s. The tension in the string will be 52 N, when the mass is at (g=10m/s2)
View SolutionTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
View Solution
