If a missile is propelled horizontally with 20 m/s from some height, what is the value of RC at t=2s?
The correct Answer is:80√2
To find the radius of curvature RC of a missile propelled horizontally with a speed of 20 m/s from a height after 2 seconds, we can follow these steps:
Step 1: Determine the horizontal and vertical velocities
The horizontal velocity vx remains constant:
vx=20m/s
For the vertical velocity vy after time t=2s, we use the equation of motion:
vy=uy+g⋅t
where:
- uy=0 (initial vertical velocity)
- g=10m/s2 (acceleration due to gravity)
- t=2s
Substituting the values:
vy=0+10⋅2=20m/s
Step 2: Calculate the net velocity
The net velocity vnet is the vector sum of the horizontal and vertical velocities:
vnet=√v2x+v2y
Substituting the values:
vnet=√(20)2+(20)2=√400+400=√800=20√2m/s
Step 3: Determine the acceleration component
The only acceleration acting on the missile is due to gravity, which acts vertically downwards. The radius of curvature RC is given by:
RC=v2neta
where a is the component of acceleration perpendicular to the velocity vector. Since the vertical and horizontal components of velocity are equal, the angle between them is 45∘. The component of gravity acting perpendicular to the net velocity is:
a=g⋅cos(45∘)=10⋅1√2=5√2m/s2
Step 4: Calculate the radius of curvature
Substituting the values into the formula for RC:
RC=(20√2)25√2=8005√2=160√2=80√2m
Final Answer
The radius of curvature RC at t=2s is:
RC=80√2m
---
vx=20m/s
vy=uy+g⋅t
where:
- uy=0 (initial vertical velocity)
- g=10m/s2 (acceleration due to gravity)
- t=2s
vy=0+10⋅2=20m/s
vnet=√v2x+v2y
Substituting the values:
vnet=√(20)2+(20)2=√400+400=√800=20√2m/s
RC=v2neta
where a is the component of acceleration perpendicular to the velocity vector. Since the vertical and horizontal components of velocity are equal, the angle between them is 45∘. The component of gravity acting perpendicular to the net velocity is:
a=g⋅cos(45∘)=10⋅1√2=5√2m/s2
RC=(20√2)25√2=8005√2=160√2=80√2m
The radius of curvature RC at t=2s is:
RC=80√2m
Topper's Solved these Questions
- CIRCULAR MOTIONBook:RESNICK AND HALLIDAYChapter:CIRCULAR MOTIONExercise:PRACTICE QUESTIONS(INTEGER TYPE)
Explore 2 Videos
- CIRCUITSBook:RESNICK AND HALLIDAYChapter:CIRCUITSExercise:Practice Questions (Integer Type)
Explore 3 Videos
- CURRENT AND RESISTANCEBook:RESNICK AND HALLIDAYChapter:CURRENT AND RESISTANCEExercise:Practice Questions (Integer Type)
Explore 3 Videos
Similar Questions
A particle is projected horizontally with a speed of 40√3m/s, from some height t=0. At what time its velocity makes 60∘ angle with initial velocity.
(g=10m/s2)

View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.
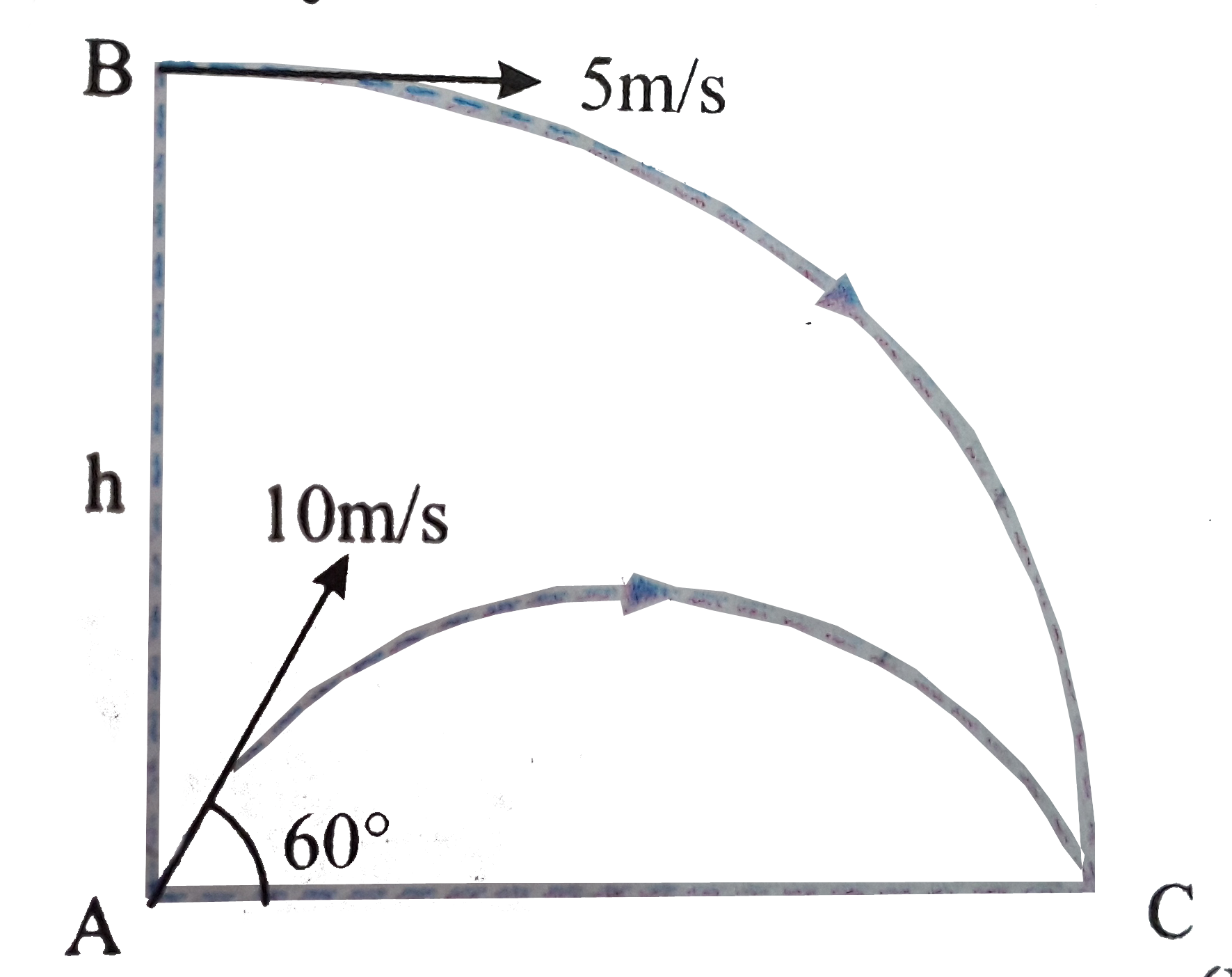
View Solution
Knowledge Check
A particle is projected horizontally with speed 20√3m/s, from some height at t=0. At what time its velocity will make 60∘ angle with initial velocity ?
A1 secB2 secC1.5 secD2.5 secA ball of mass 2 kg is projected horizontally with a velocity 20m/s from a building of height 15m. The speed with which body hits the ground is :
A20 m/sB10(7)1/2m/sC25 m/sD35 m/sTwo particles are projected horizontally with same speed 30m/s but in opposite directions from same height at time t=0. Calculate angle between velocity vectors of particles at time t=3s.
A0∘B30∘C60∘D90∘
A ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Time taken by the ball to strike the ground is
View SolutionA ball is thrown horizontally with speed 10m/s from the top of tower of height 80m. After how much time and at what horizontal distance from the tower it strikes the ground ?
View SolutionA particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m/s. If g=10m/s2, then find the :-
View SolutionA ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
velocity with which the ball strikes the ground is .
View SolutionA ball is thrown horizontally with a speed of 20m/s from the top of a tower of height 100m
Horizontal distance travelled by the before it strickes the ground is
View Solution

