Two point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.
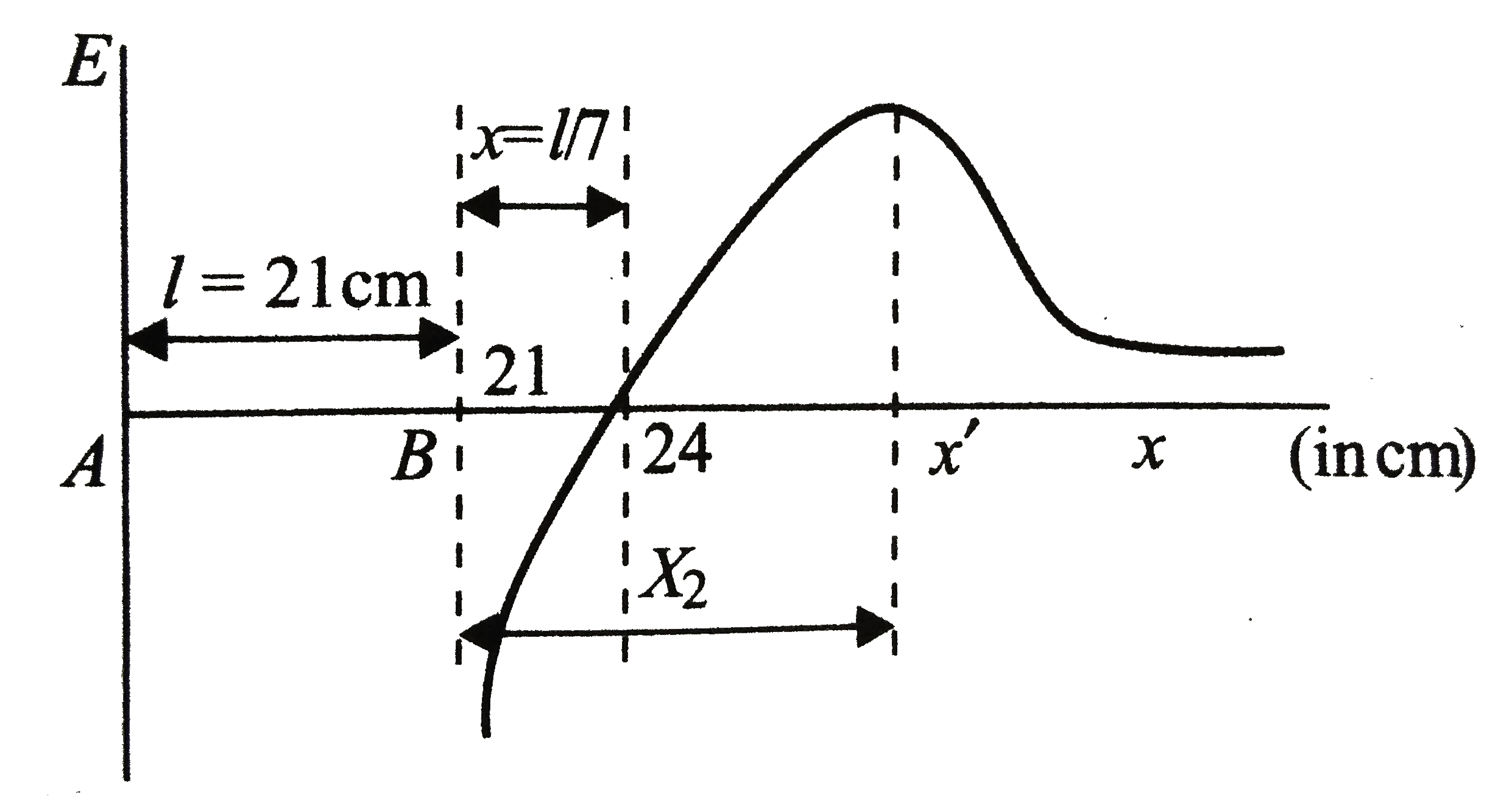
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.
l(l+x1x1)23−1
l(l+x1x1)13−1
l(l+2x1x1)23−1
l(l+2x1x1)13−1
The correct Answer is:A
∵ Electric field near point b is −∞
∴'b' shluld be negative electric field at x1 is O which possible only if 'a' and 'b' are of opposite sign
∴'a' is positive
Charge b is negative and charge a is positive

E at A=0(A=)E=2)
⇒|Qa|(l+x1)2=|Qb|(x1)2
∣∣∣QaQb∣∣∣=(l+x1x1)2=(1+lx1)2
W at a general X
K|Qa|(l+x2)−K|Qb|(x2)
=K|Qa|{1(l+x)2−∣∣∣QbQa∣∣∣1x2}
If E is a maximum, dEdx=0
⇒−2(l+x)3+(x1l+x1)22x3=0
(l+x)2=x3(l+x1x1)2
l+x=x(l+x1x1)23
x2=l(l+x1x1)23−1
x2=l(l+x1x1)23−1,∣∣∣QaQb∣∣∣=(1+lx1)2
Charge b is negative and charge a is positive.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.31
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.32
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.29
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Two point charge Qa and Qb are positional at point A and B. The field strenght to the right of charge Qb on the line that passes therough the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincedes with the positive direction of the x-axis. The distance between the charges is l=21cm.

(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strenght is maximum.
View SolutionTwo points like charges QA and QB are positioned at points a and B (see figure). The electric field strength to the right of charge QB on the line that passes through the two charges varies according to a law that is represented schematically in Figure below accompaanying the problem without employing a definite scale. Assume electric field to be positive if its direct ion coincides with (the positive direction on the x-axis. THe distance between the charges is l.
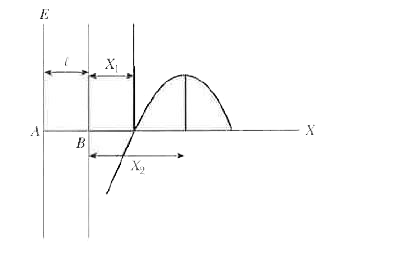

View Solution
Knowledge Check
The positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
A→r1√q1+→r2√q2√q1+√q2B→r1√q2+→r2√q1√q1+√q2C→r1√q2+→r2√q1√q1+q2D→r1√q1+→r2√q2√q1+q2Two fixed charges 4Q (positive) and Q (negative) are located at A and Bthe distance AB being 3m
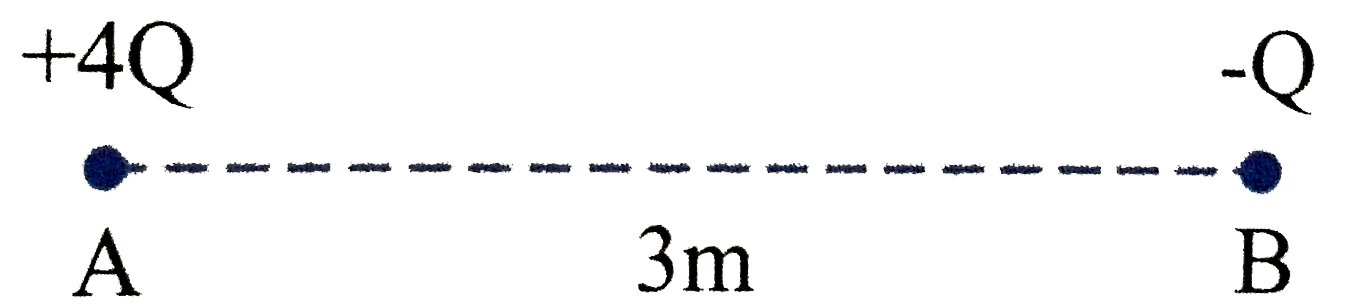 AThe point P where the resultant field due to both is zero is on AB outside ABBThe point P where the resutlant field due to both is zero is on AB inside ABCIf a positive charge is placed at P and displaced slightly along AB it will execute oscillations.DIf a negative charge is placed at P and displaced slightly along AB it will execute oscillations.
AThe point P where the resultant field due to both is zero is on AB outside ABBThe point P where the resutlant field due to both is zero is on AB inside ABCIf a positive charge is placed at P and displaced slightly along AB it will execute oscillations.DIf a negative charge is placed at P and displaced slightly along AB it will execute oscillations.Two equal negative charges are fixed at points and on y-axis. A positive charge Q is released from rest at the point on the x-axis. The charge Q will:
Aexecute simple harmonic motion about the originBmove to the origin and remain at restCmove to infinityDsame as at point 25 cm aways form the surface
Two point charges Q1 and Q2 are positioned at points I and 2. The field intensity to the right of the charge Q2 on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
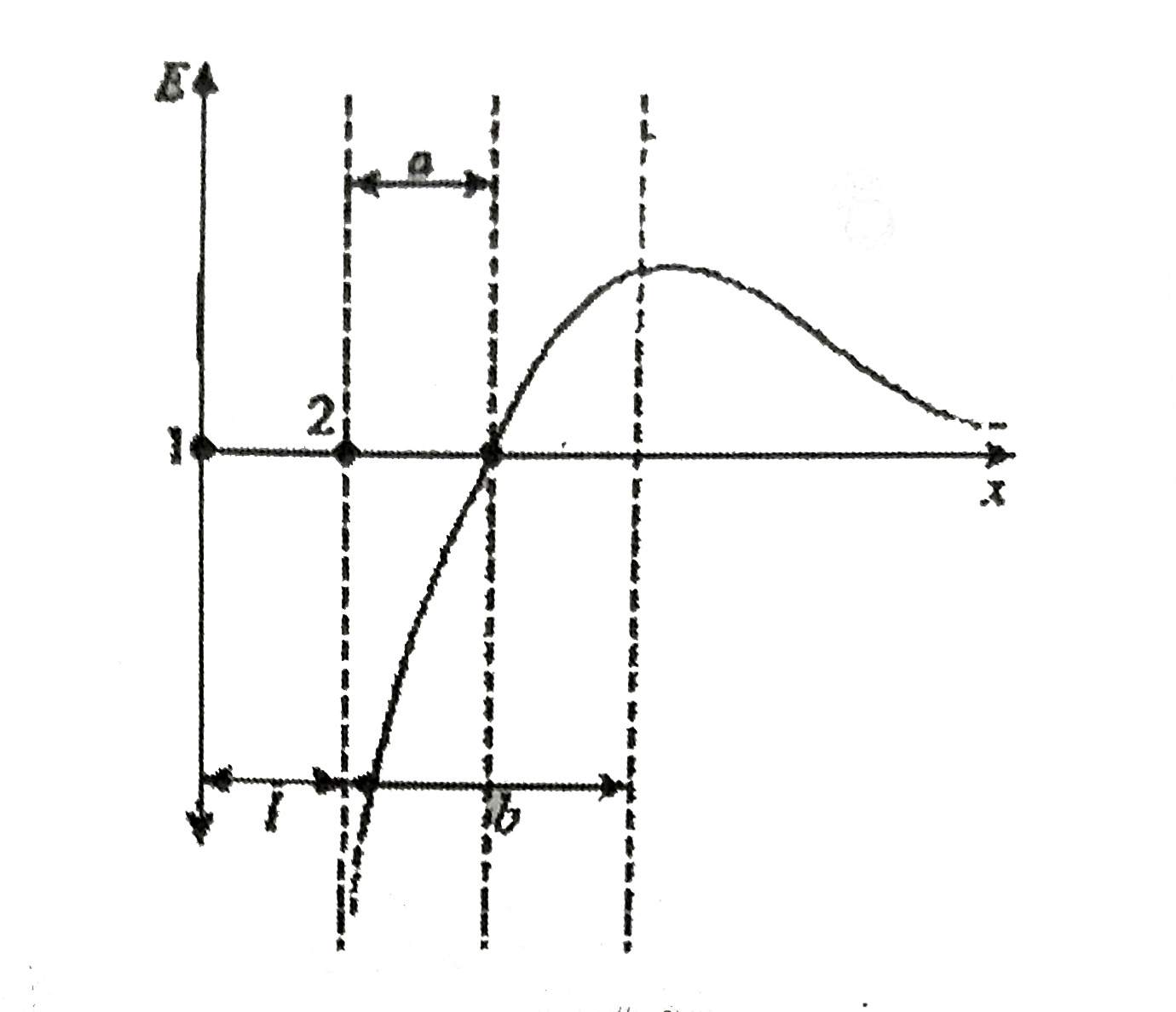
(a) Find the sign of each charge
(b) Find the ratio of the absolute values of the charges ∣∣∣Q1Q2∣∣∣
(c) Find the value of b where the field intensity is maximum
[(a) Q2 is negative and Q1 is positive (b) (l+aa)2, (c) l(l+aa)2/3−1⎤⎥ ⎥ ⎥⎦
View SolutionTwo point-like charges a and b whose strengths are equal in absolute value are positioned at a certain distance from each other. Assuming the field strength is positive in the direction coinciding with the positive direction of the r axis, determine the signs of the charges for each distribution of the field strength between the charges shown in Figures (a),(b),(c),and(d).
View SolutionTwo equal like charges are positioned at a certain distance from each other. How do the electric field strength and the potential vary along the axis that passes through the midpoint of the distance between the charges at right angles to the line connecting the charges?
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionTwo charge +q and −q are kept apart.then at any point on the right beisector of line joining the two charges
View Solution

