Two blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .
.
Maximum extension in the spring is 4MgK
Maximum kinetic energy of the stystem is 2M2g2K
Maximum energy stored in the spring is four times that of maximum kinetic energy of the system.
When kinetic energy of the system is maximum, energy stored in the spring is 4M2g2K
The correct Answer is:A, B, C
Maximum extension will be at the moment when both masses stop momentarily after going down Applying W-E theorem from starting to that instant.
kf−ki=Wgr+Wsp+Wten
0−0=2M.gx+(−12kx2)+0x=4MgK
System will have maximum KE when net force on the system becomes zero. Therefore
2Mg=TandT=kx⇒x=2MgK
Hence KE will be maximum when 2M mass has gone down by 2MgK
Applying W.E theorem
kf−0=2Mg.2MgK−12K4M2g2K2
Kf=2M2g2K2
Maximum energy of strong
=12K.(4MgK)2=8M2g2K
Therefore Maximum spring energy
=4× maximum K.E
When K.E is maximum x=2MgK
Spring energy =12.K.4M2g2K2
=2M2g2K2 i.e. (D) is wrong.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.31
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.32
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.29
20 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
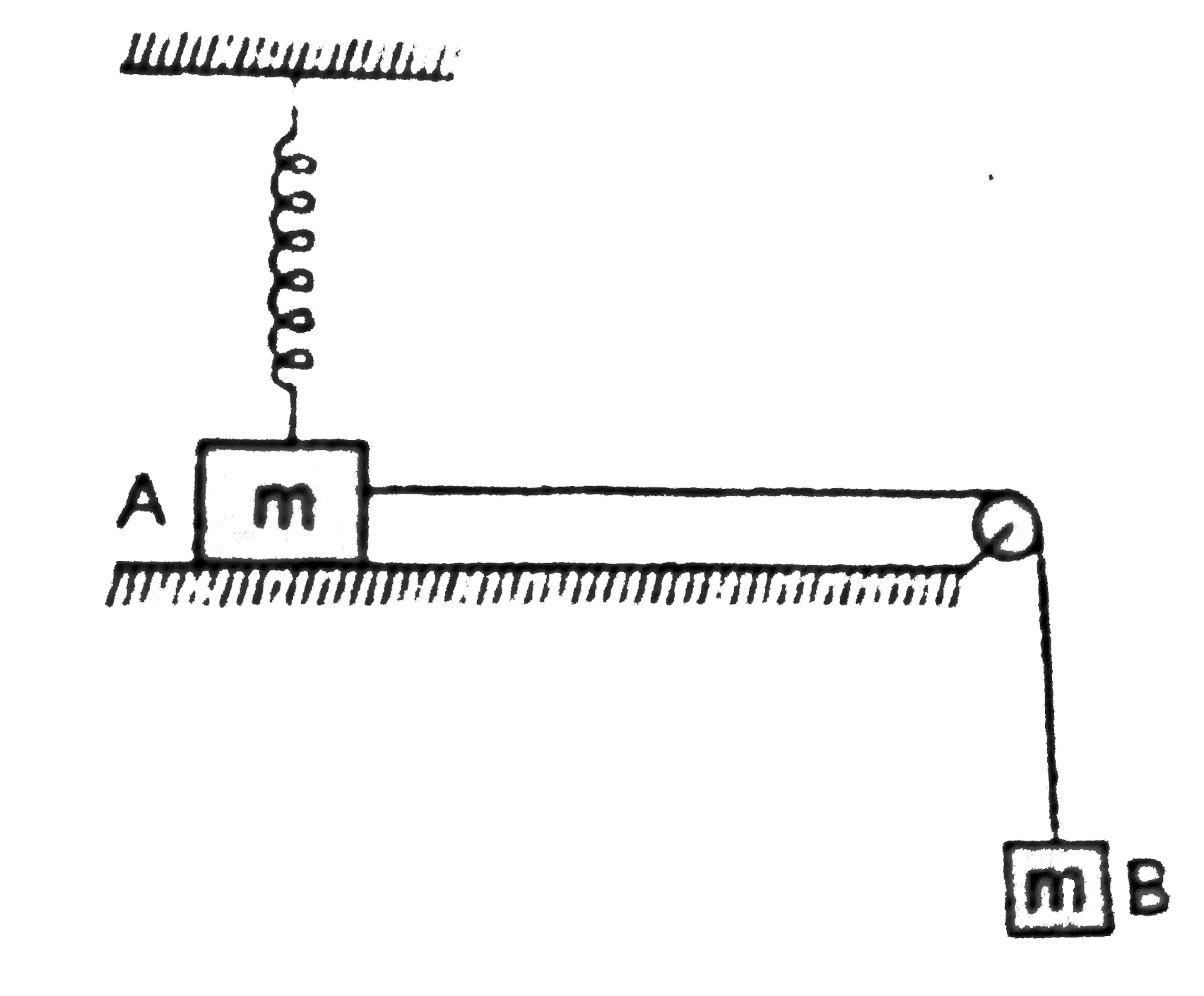
Figure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of theseTwo block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
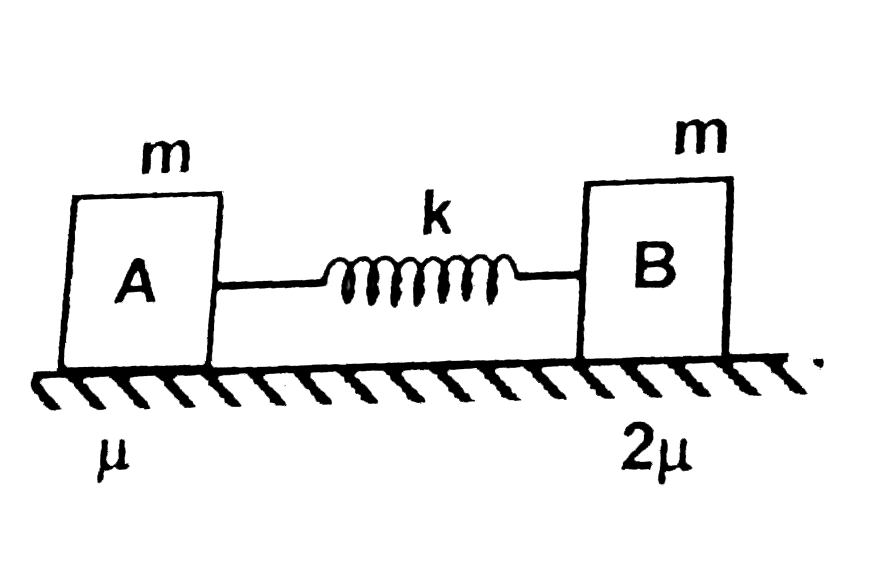 A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
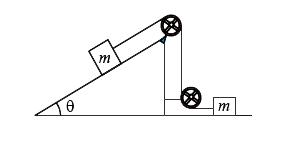
Two blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionTwo blocks of masses m, and m, are connected to the ends of a spring of spring constant k. System is kept at rest on a frictionless horizontal floor with spring in its natural length. Both the blocks are pulled along opposite directions with forces of same magnitude F. Calculate maximum elongation of spring and distances travelled by the blocks during this motion.
View Solution
