The displacement 'x' and time of travel 't' for a particle moving an a straight line are related as t=√(x+1)(x−1). Its acceleration at a time t is
1x−1x2
1x3
−t2x3
−tx2
The correct Answer is:B
t2=x2−1
x2=1+t2
xdxdt=t
⇒(dxdt)2+xd2xdt=1
⇒xd2xdt2=1−(dxdt)2=1−(tx)2
=x2−t2x2=1x2⇒a=d2xdt2=1x3.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.10
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.11
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.8
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Figure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t=t1andt=t2.

View SolutionThe diagram shows the displacement - time graph for a particle moving in a straight line. The distance (in m) coverted by the particle in the time interval t=0 to t=5s is

View Solution
Knowledge Check
The displacement 'x' of a particle moving along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is :-
Aa1Ba2C2a2D3a2The position of a particle moving on a straight line depends on time t as
x=(t+3)sin(2t)AIts velocity at the initial moment is 6 m/sBIts acceleration at the initial is −8m/s2CIt has velocity of 3 m/s at t=π2 secDIt has an acceleration of 2m/s2 at t=π4 secFor a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
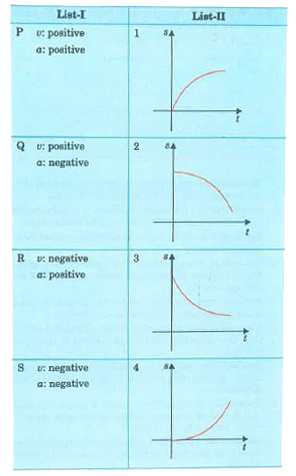 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132
The displacement x of a particle along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is
View SolutionThe displacement x of a particle along a straight line at time t is given by x=a0−a1t+a2t2 . The acceleration of the particle is -
View SolutionThe velocity -time (v−t) graph of a particle moving in a straight line is shown in figure. The acceleration of the particle at t=9 is:
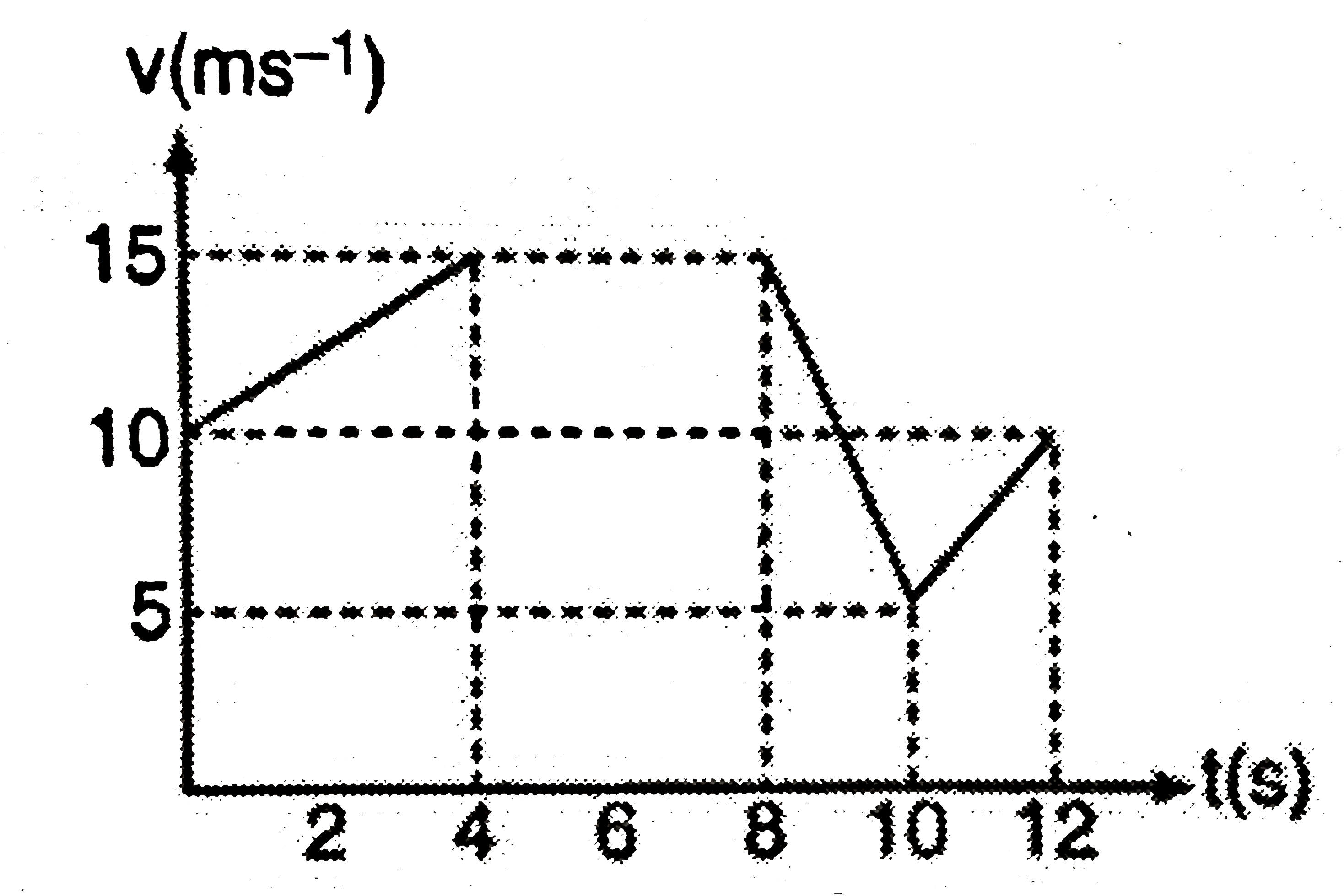
View SolutionThe displacement x of a particle along a straight line at time t is given by : x=a0+a1t2+a23t2. The acceleration of the particle is
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View Solution
