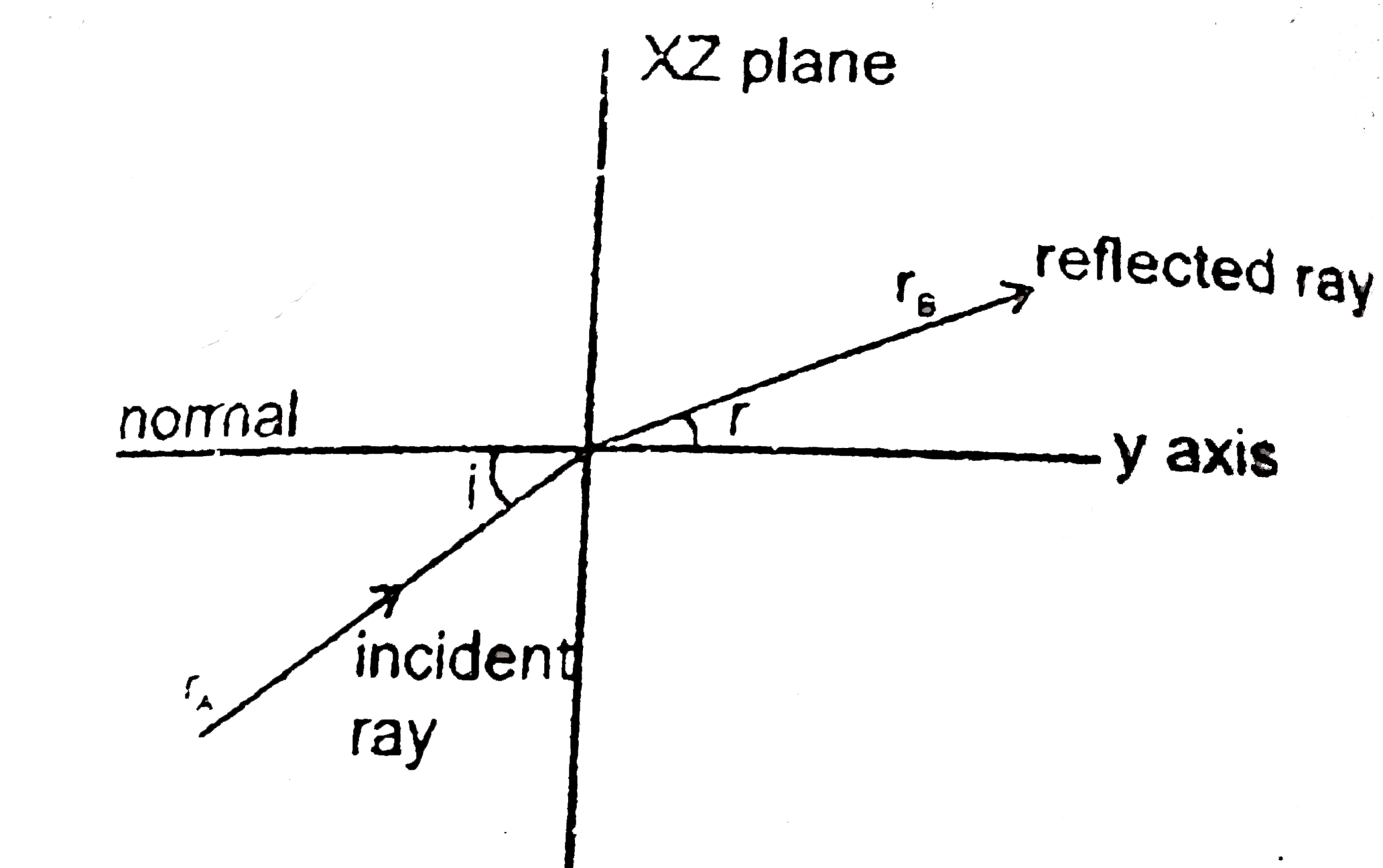
The $x z$ plane separates two media $A$ and $B$ with refractive indices $μ_{1}$ & $μ_{2}$ respectively. A ray of light travels from $A$ to $B$ . Its directions in the two media are given by the unut vectors, ${\to r}_{A} = a ˆ i + b ˆ j$ & ${\to r}_{B} α ˆ i + β ˆ j$ respectively where $ˆ i$ & $ˆ j$ are unit vectors in the $x$ & $y$ directions. Then :

$μ_{1} a = μ_{2} α$

$μ_{1} α = μ_{2} a$

$μ_{1} b μ_{2} β$

$μ_{1} β = μ_{2} b$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

The x-z plane separates two media A and B of refractive indices $μ_{1} = 1.5$ and $μ_{2} = 2$ . A ray of light travels from A to B. Its directions in the two media are given by unit vectors $u_{1} = a ˆ i + b ˆ j$ and $u_{2} = c ˆ i + a ˆ j$ . Then
A $\frac{a}{c} = \frac{4}{3}$
B $\frac{a}{c} = \frac{3}{4}$
C $\frac{b}{c} = \frac{4}{3}$
D $\frac{b}{d} = \frac{3}{4}$
The unit vector parallel to the resultant of the vectors $\to A = ˆ i + 2 ˆ j - ˆ k$ and $\to B = 2 ˆ i + 4 ˆ j - ˆ k$ is
A $\frac{1}{49} (7 ˆ i + 6 ˆ j - 2 ˆ k)$
B $\frac{1}{7} (3 ˆ i + 6 ˆ j - 2 ˆ k)$
C $\frac{1}{49} (3 ˆ i + 6 ˆ j - 2 ˆ k)$
D $\frac{1}{7} (7 ˆ i + 6 ˆ j - 2 ˆ k)$
The unit vector perpendicular to $\to A = 2 ˆ i + 3 ˆ j + ˆ k$ and $\to B = ˆ i - ˆ j + ˆ k$ is
A $\frac{4 ˆ i - ˆ j - 5 ˆ k}{\sqrt{42}}$
B $\frac{4 ˆ i - ˆ j + 5 ˆ k}{\sqrt{42}}$
C $\frac{4 ˆ i + ˆ j + 5 ˆ k}{\sqrt{42}}$
D $\frac{4 ˆ i + ˆ j - 5 ˆ k}{\sqrt{42}}$