A block of dimensions $a \times a \times 2 a$ is kept on an inclined plane of inclination $37^{\circ}$ . The longer side is perpendicular to the plane. The co $-$ efficient of friction between the block and the plane is $0.8 .$ By numerical analysis find whether the block will topple or not.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:Since torque is not balanced , it will topple .

If ever it will topple , it will topple about $A$ . It can be verified that the block is not sliding.
Now, $τ_{A} = m g sin θ \times a - m g cos θ \times \frac{a}{2}$

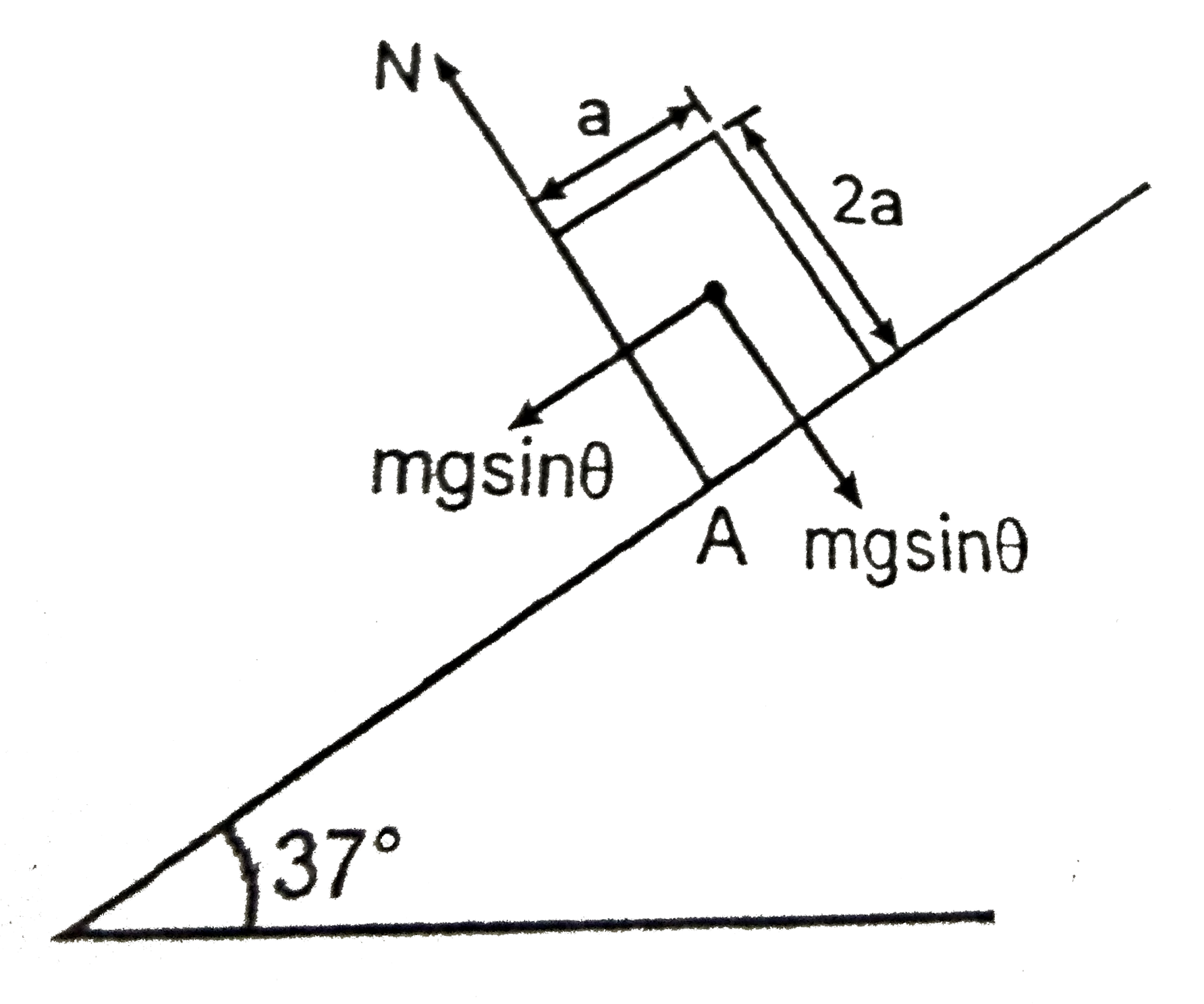
$= τ_{A} = \frac{m a g}{5}$ which is non $-$ zero.
Since torque is not balanced, it will topple .

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is $μ$ then
.
A $μ > tan θ$
B $f = m g sin θ$
C $f = μ m g cos θ$
Dthe reaction of the ground on the block is mg cos $θ$
Question 2 - Select One
A block of mass m slides down an inclined plane of inclination $θ$ with uniform speed. The coefficient of friction between the block and the plane is $μ$ . The contact force between the block and the plane is
Amg
B $m g sin θ \sqrt{1 + μ^{2}}$
C $m g sin θ$
D $\sqrt{{(m g sin θ)}^{2} + {(μ m g cos θ)}^{2}}$
Question 3 - Select One
A block of mass m slides down an inclined plane of inclination $θ$ with uniform speed The coefficient of friction between the block and the plane is $μ$ . The contact force between the block and the plane is .
A $m g sin θ \sqrt{1 + μ^{2}}$
B $\sqrt{{(m g sin θ)}^{2} + {(μ m g cos θ)}^{2}}$
C $m g sin θ$
D $m g$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 68

Home
Ask Doubt
Profile