A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

g2
√3g2
g√2
g√5
The correct Answer is:C
x2=4ay Differenctiating w.r.t.y, we get
dydx=x2a
∴ At (2aa,a),dydx=1
⇒hence θ=45∘
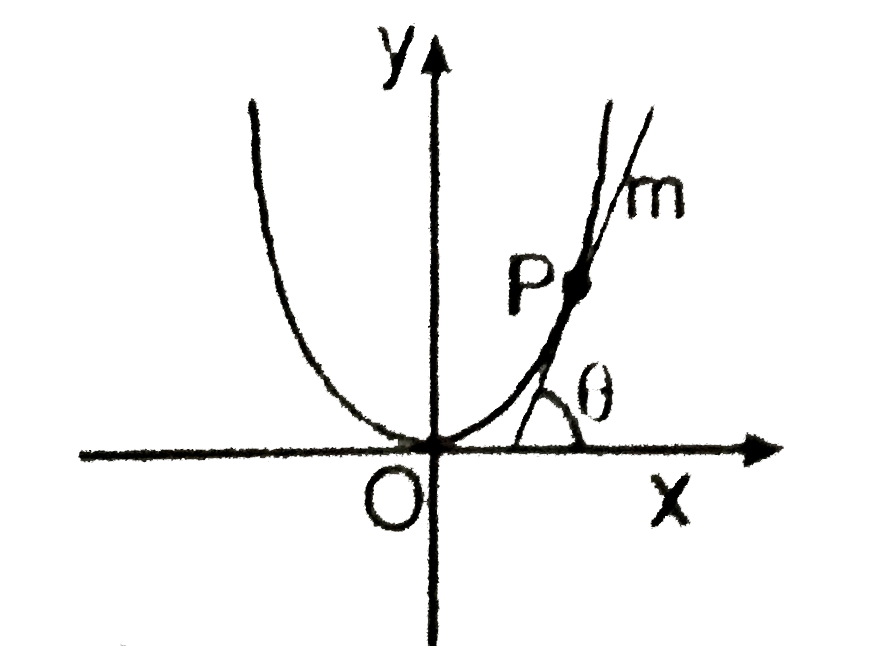
the component of weight along tangential direction is mgsinθ
hence tangential acceleration is gsinθ=g√2
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 46
Explore 6 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 47
Explore 7 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 44
Explore 5 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
A bead is free to slide down on a smooth wire rightly stretched between points AandB on a vertical circle of radius 10m. Find the time (in sec) taken by the bead to reach point B, if the bead slides from rest from the highest point A on the circle.
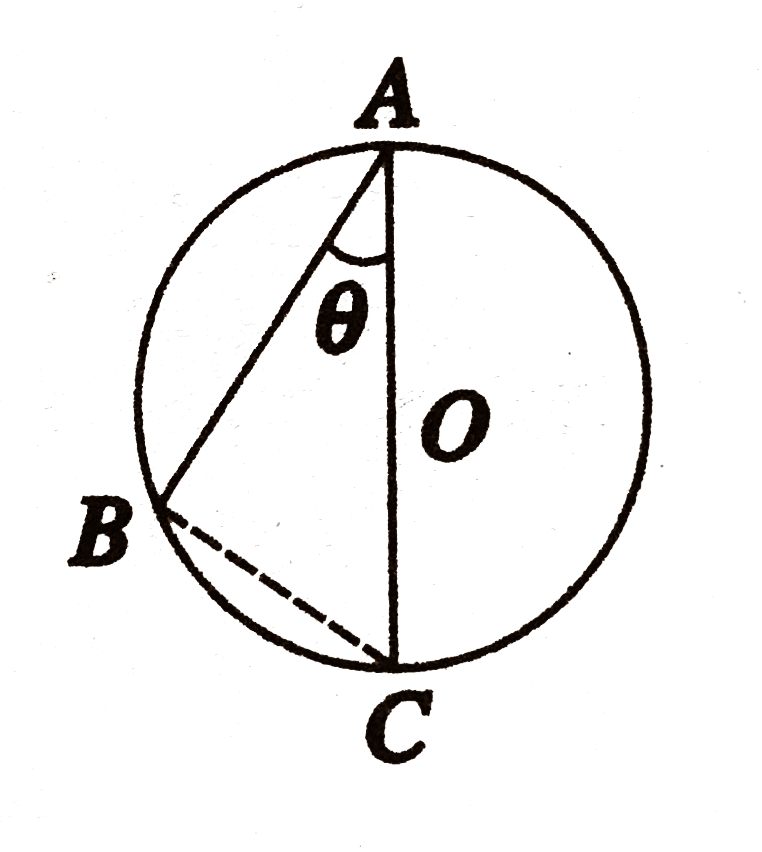 .
.
View SolutionA bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View Solution
Knowledge Check
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is x2=4ay . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :
 Ag2B(√3g)(2)Cg√2Dg
Ag2B(√3g)(2)Cg√2Dg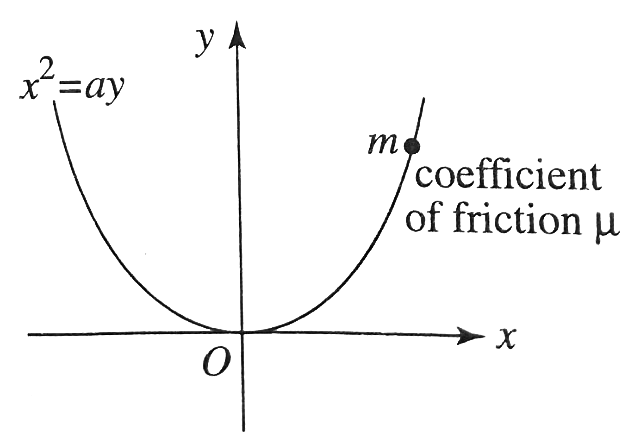
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium isAμaBμ2aC14μ2aD12μa
A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downwards as in figure and whose equation is x2=ay. If the coefficient of friction is μ, the highest distance above the x-axis at which the particle will be in equilibrium isAμaBμ2aCμ2a4D2μa
A bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
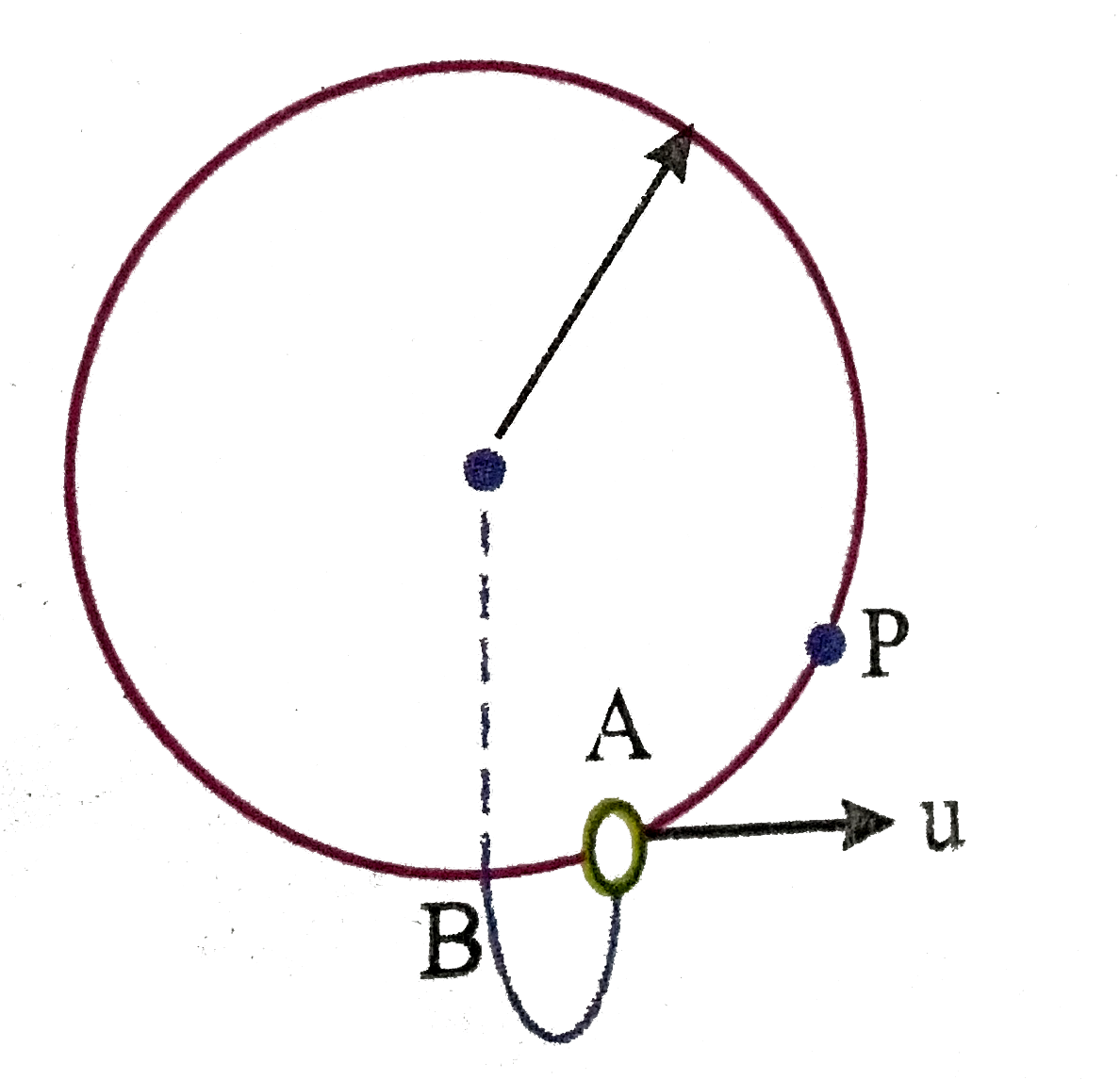
If v=2u0, the tension T in th elastic string when the bead is at the highest point B of the wire is
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
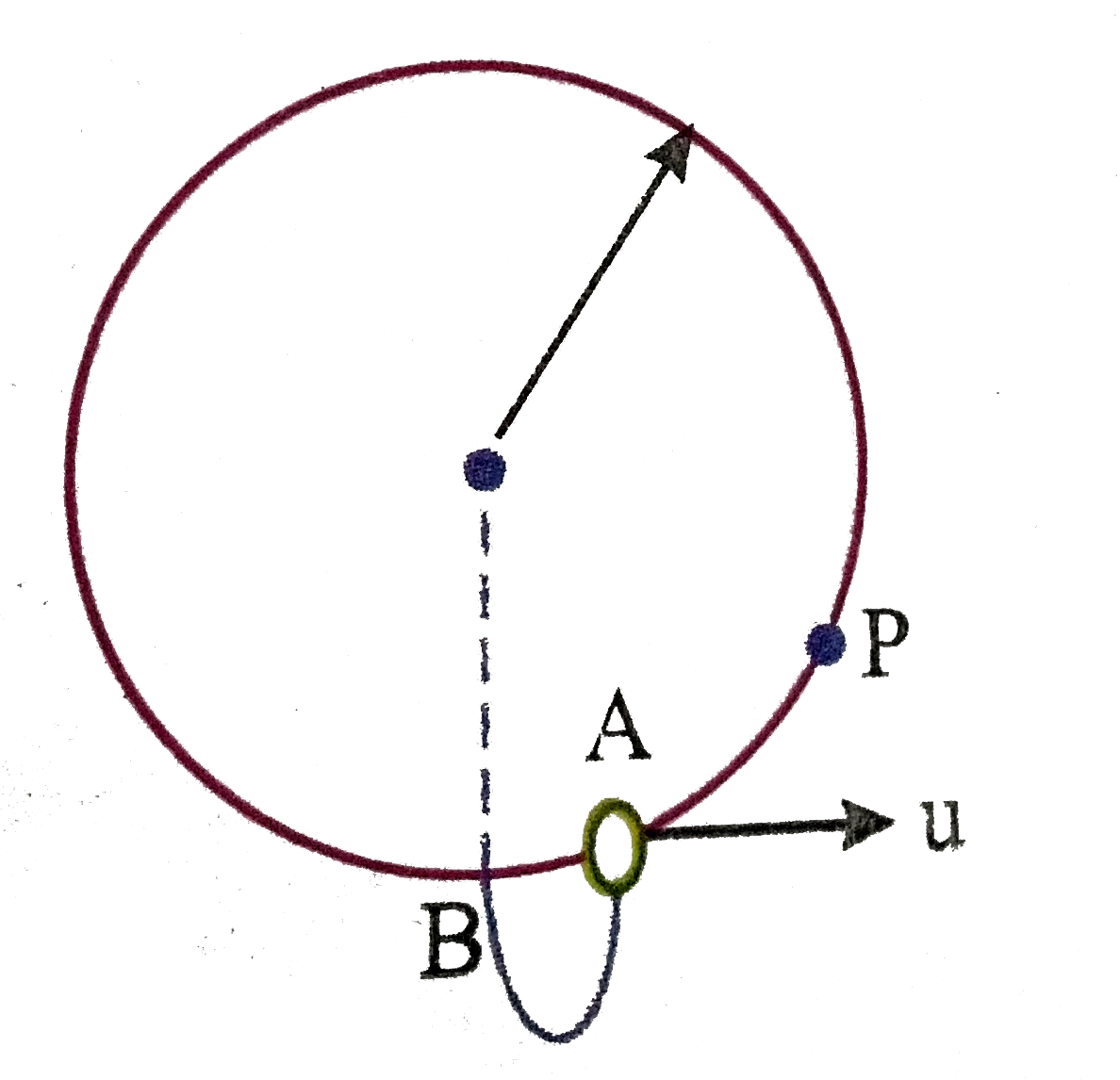
The smallest value u0 of u for which the bead will make complete revolutions of the wire will be
View Solution

