Two cars A andB are racing along straight line. Car A is leading, such that their relative velocity is directly proportional to the distance between the two cars. When the lead of car A is l1=10m , its running 10m/s faster than car B. Determine the time car A will take to increase its lead to l2=20m from car B.
The correct Answer is:t=(loge2)sec
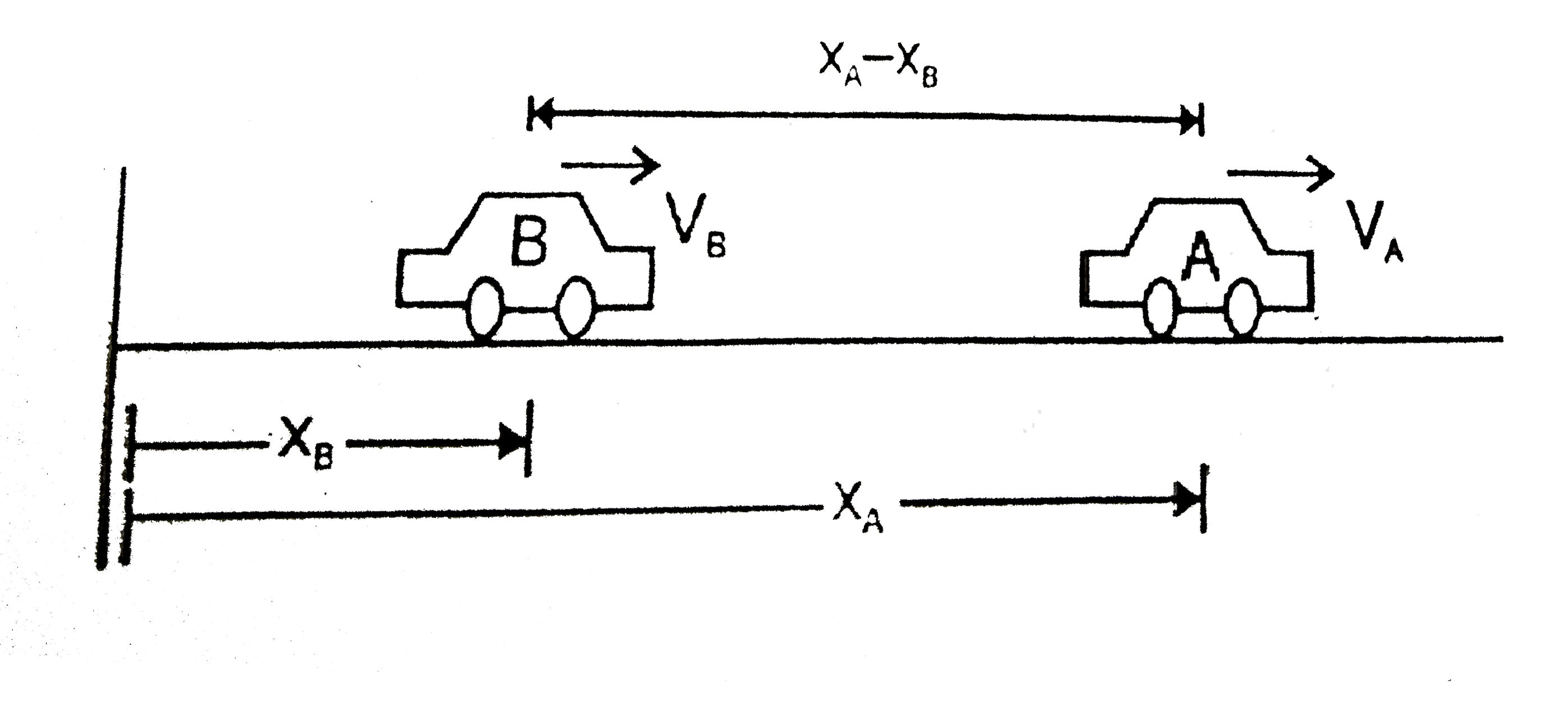
As given
(VA−VB)∝xA−xB
(VA−VB)=K(xA−xB)
when xA−xB=10 We have VA−VB=10
We get
10=K10⇒K=1
rArVA−VB=(xA−xB)......(1)
Now let
xA−xB=y...............(2)
On differentiating with respect to 't' on both side.
⇒dxAdt−dxBdt=dydt⇒VA−VB=dydt.......(3)
⇒ Using (1),(2),(3)
We get dydt=y
Here y represents separation between two cars
20∫10dyy=t∫0dt⇒[logey]2010=t
t=(loge2)sec Required Answer.
. 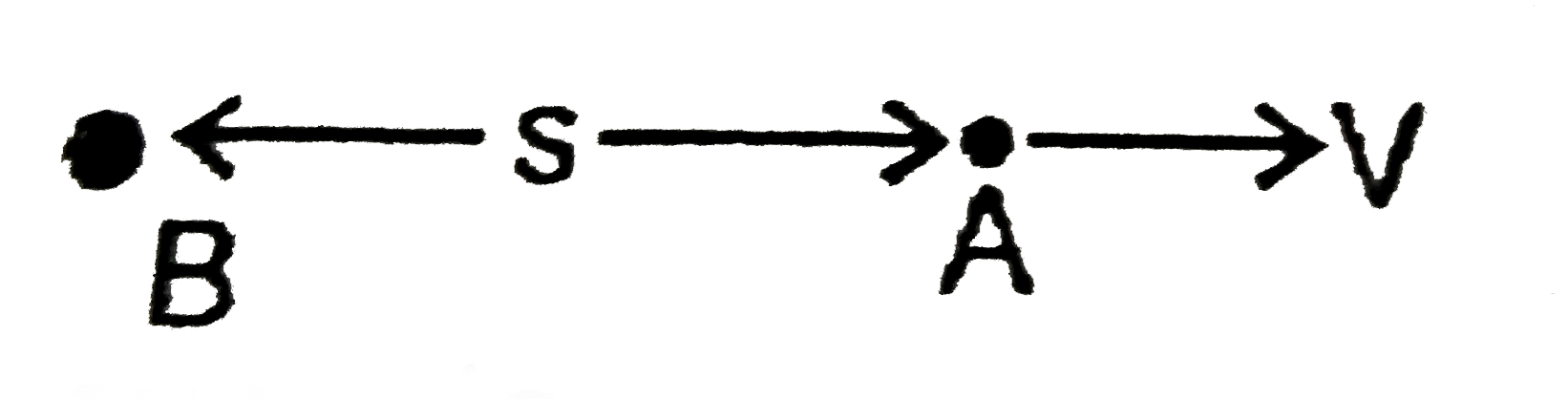
Alter. (Assuem to be at rest)
V∝s
V=ks
V=10,s=10,k=
dsdt=s,20∫10dss=t∫0dt
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 20
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 21
Explore 8 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCEChapter:DAILY PRACTICE PROBLEMSExercise:dpp 18
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 54 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCEChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
Two cars A and B are moving on parallel roads in the same direction. Car A moves with constant velocity 30m/s and car B moves with constant acceleration 2.5m/s2 . At , car A is ahead of car B and car B is moving with 12m/s velocity . The distance travelled by car B until it overtakes car A is
View SolutionCar A overtakes car B with relative velocity of 40 m/s with what velocity car A appearing in the mirror (f = 10 cm) of car B 1.9m far from it.
View Solution
Knowledge Check
Two cars A and B are running at velocities of 60 km/h and 45 km/h. What is the relative velocity of car A with respect to car B, if both are moving eastward ?
A15 km/h,B45 km/hC60 km/h,D105 km/h.Two cars A and B are at rest at the origin O. If A starts with a uniform velocity of20m/s and B starts in the same direction with a constant acceleration of 2m/s2, then the cars will meet after time
A10sB20sC30sD40sA car is travelling along a flyover bridge which is a part of vertical circle of radius 10m. At the highest point of it the normal reaction on the car is half of it’s weight, the speed of car is
A7m/sB10m/sC14m/sD20m/s
Two cars A and B move on a straight road for the same time. Car A covers 80 m and car B covers 100 m. Which one of the two is faster?
View SolutionA car is travelling along a straight line and covers one-fourth of the total distance with a velocity of 10m/s. the remaining distance is covered with a velocity of 5m/s. calculate the average velocity of the car.
View Solution6 cars- M, N, O, P, Q and R are parked in a straight line not necessarily in the same order. Distance between each car is successive multiple of 3 but not necessarily in the order. The distance between car N and car O is 36m and no car is parked between them. The distance between car M and car O is 102m. Car R is 99m to the right of car N. Only one car is parked between car O and car R. Car M is parked to the immediate left to car P. The distance between car M and car P is 12m more than the distance between car P and car N. The distance between R and M is more N. The distance between R and M is more than 60m. The distance between car P and car Q is 93m. If car Q moves 20m to the north then takes a left turn and moves 50m then again takes a left turn and moves for 10m and stops at point Z. Car A is 16m to the west of point Z. Car A moves 66m towards west and stops at point Y.
What is the maximum distance between two cars?
View Solution6 cars- M, N, O, P, Q and R are parked in a straight line not necessarily in the same order. Distance between each car is successive multiple of 3 but not necessarily in the order. The distance between car N and car O is 36m and no car is parked between them. The distance between car M and car O is 102m. Car R is 99m to the right of car N. Only one car is parked between car O and car R. Car M is parked to the immediate left to car P. The distance between car M and car P is 12m more than the distance between car P and car N. The distance between R and M is more N. The distance between R and M is more than 60m. The distance between car P and car Q is 93m. If car Q moves 20m to the north then takes a left turn and moves 50m then again takes a left turn and moves for 10m and stops at point Z. Car A is 16m to the west of point Z. Car A moves 66m towards west and stops at point Y.
What is the distance between car P and car R?
View SolutionTwo cars A and B start moving from the same point with same velocity v=5km/minute. Car A moves towards North and car B in moving towards East. What is the relative velocity of B with respect to A ?
View Solution

