अनंत लम्बाई के किसी सीधे कुचालक तार पर एकसमान रूप से आवेश वितरण के कारण इसका रैखिक घनत्व $λ$ है | एक सिरे से लाम्बिक दुरी R पर परिणामी विद्युत - क्षेत्र के लिए व्यंजक प्राप्त करे |

Video Solution

Text Solution

Verified by Experts

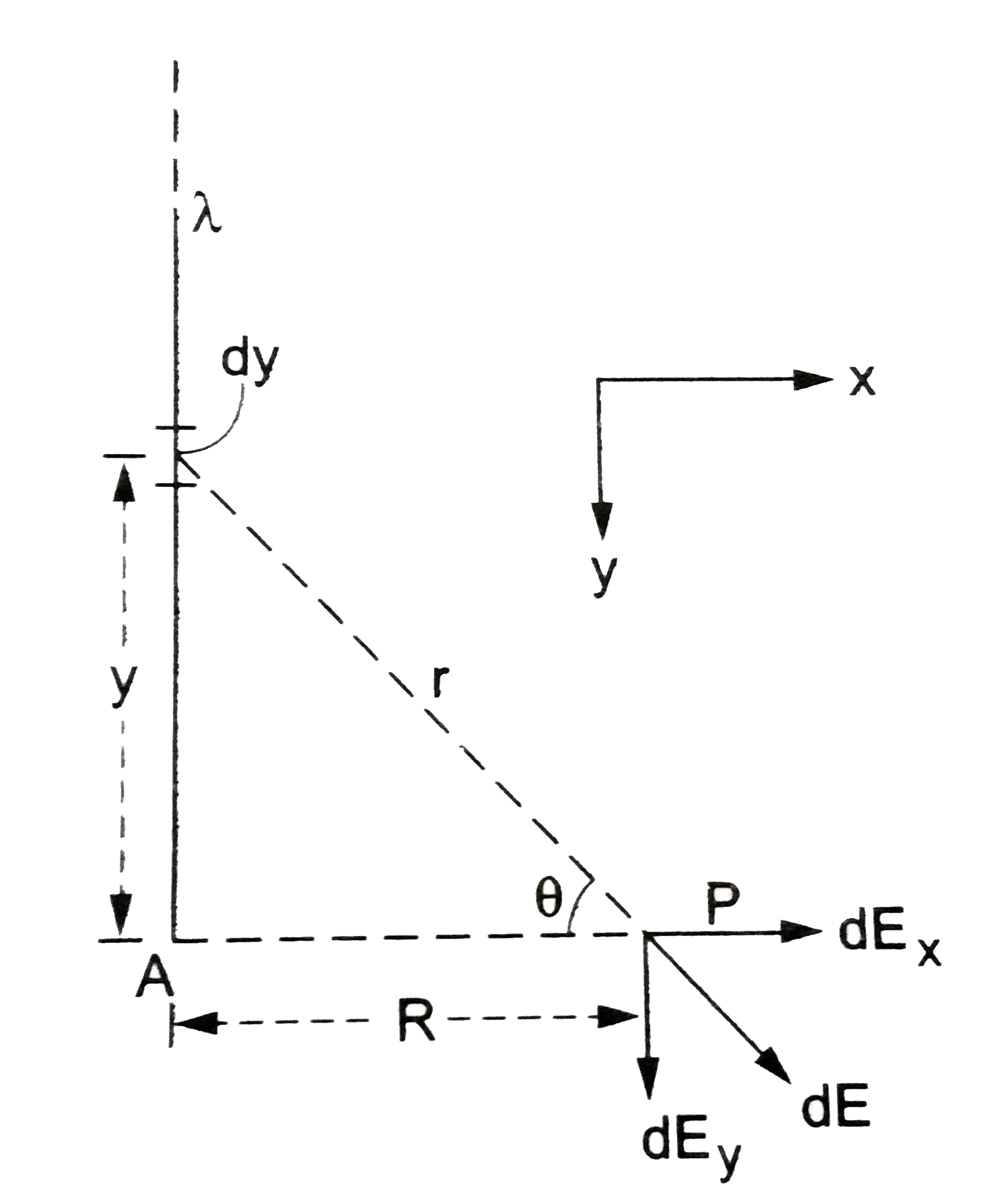
चित्र में A से y दुरी पर अल्पांश dy पर आवेश dq = $λ d y$ के कारण बिंदु P पर विद्युत् -क्षेत्र का परिमाण, $d E = \frac{1}{4 π \in_{0}} \frac{λ d y}{r^{2}}$
इस क्षेत्र का x - घटक $d E_{x} = d E cos θ$
तथा y - घटक $d E_{y} = d E sin θ$
समाकलन करने पर, $E_{x} = \int d E_{x} = \frac{1}{4 π \in_{0}} \int \frac{λ d y}{r^{2}} cos θ$ ... ( 1)
चित्र से, $y = R tan θ$ या $d y = R {sec}^{2} θ d θ$
तथा $r = R sec θ$ या $r^{2} = R^{2} {sec}^{2} θ$
dy तथा $r^{2}$ के मान समीकरण (1 ) में रखने पर,
$E_{x} = \frac{λ}{4 π \in_{0}} \int_{0}^{π / 2} \frac{R {sec}^{2} θ d θ}{R^{2} {sec}^{2} θ} \cdot cos θ$
$= \frac{λ}{4 π \in_{0} R} \int_{0}^{π / 2} cos θ d θ$
$= \frac{λ}{4 π \in_{0} R} {[sin θ]}_{0}^{π / 2} = \frac{λ}{4 π \in_{0} R}$
इसी प्रकार, $E_{y} = \frac{λ}{4 π \in_{0} R}$
$∴$ बिंदु P पर परिणामी विद्युत् - क्षेत्र का परिमाण
$E = \sqrt{E_{x}^{2} + E_{y}^{2}} = \frac{\sqrt{2} λ}{4 π \in_{0} R}$
$∵ E_{x} = E_{y}$ , अतः क्षेत्र E की दिशा x - अक्ष से $45^{\circ}$ का कोण बनाएगी |

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

BHARATI BHAWAN-विद्युत-क्षेत्र : गॉस का प्रमेय तथा उसके अनुप्रयोग-उदाहरण

Home
Ask Doubt
Profile