गॉस के प्रमेय का उपयोग किये बिना एकसमान रूप से आवेशित अनंत लम्बा के पतले तार के कारन विद्युत् - क्षेत्र के लिए सूत्र प्राप्त करे | तार पर आवेश का रैखिक घनत्व ( linear density ) $λ$ है |

Video Solution

Text Solution

Verified by Experts

मान लिया कि अंनत लम्बाई के आवेशित तार के कारण r दुरी पर स्थित बिंदु P पर विद्युत -क्षेत्र ज्ञात करना है |
P से तार पर खिंचा गया अभिलम्ब OP है,
जहाँ $O P = r$ अब $O$ से y दुरी पर dy लम्बाई के अल्पांश AB पर आवेश $d q = λ d y$ . इस आवेश के कारण बिंदु P पर विद्युत् - क्षेत्र
$d E = \frac{1}{4 π \in_{0}} \frac{λ d y}{z^{2}}$ जहाँ $z$ = अल्पांश AB की P से दुरी | अब $- \to d E$ का OP के समांतर घटक $d E_{||} = d E cos θ$ तथा लंबवत दिशा में घातक $d E_{⊥} = d E sin θ$ .

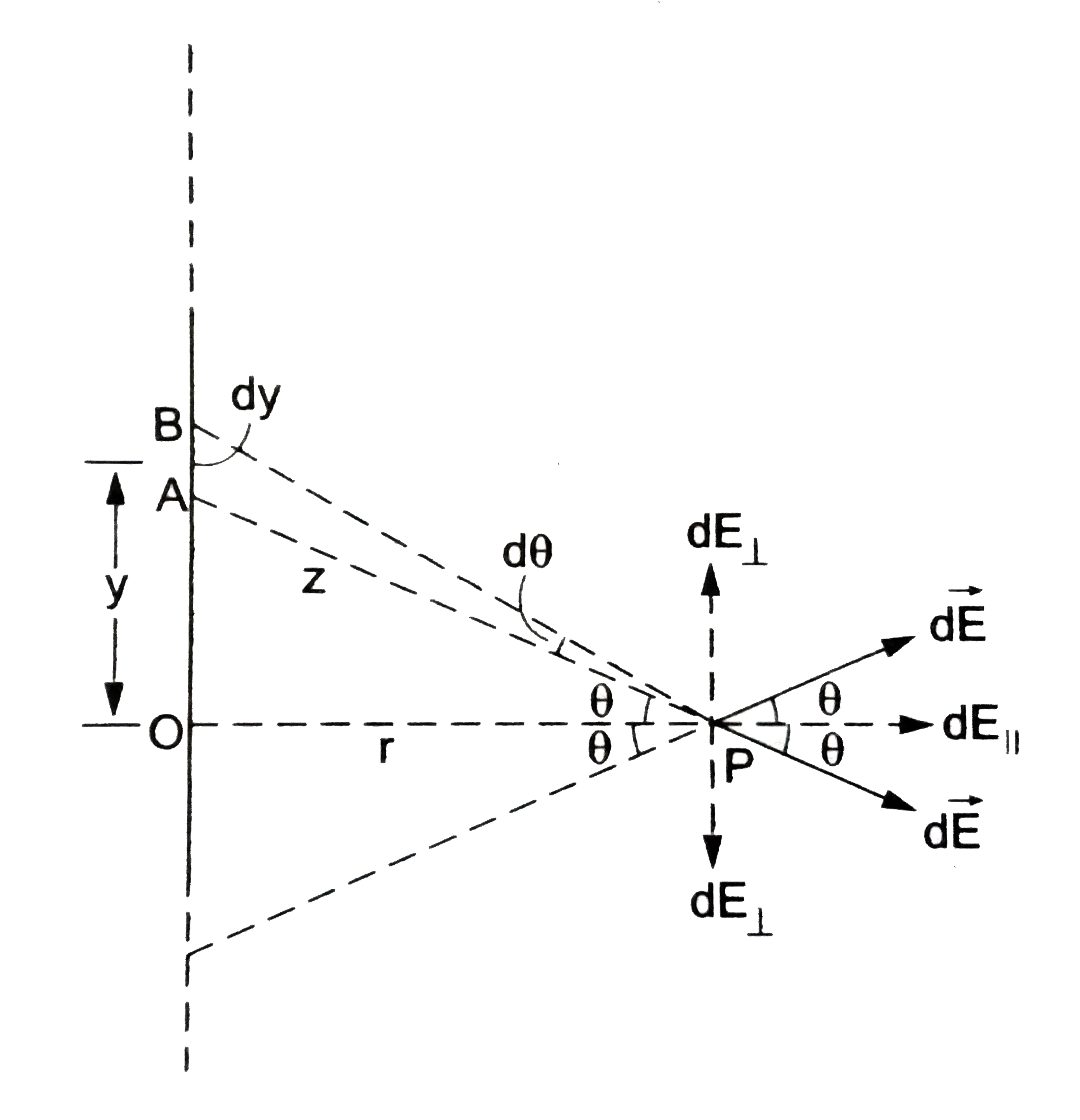
अब, बिंदु $O$ के नीचे y दुरी पर अल्पांश dy के कारण P पर क्षेत्र $- \to d E$ के भी दो घातक $d E_{||}$ तथा $d E_{⊥}$ होंगे | लंबवत घटक एक - दूसरे से निष्फल (neutralize ) हो जाएँगी तथा P पर परिणामी क्षेत्र O से P की दिशा में होगा | अतः परिणामी क्षेत्र ,
$E_{||} = \int d E_{||} = \int d E cos θ = \frac{1}{4 π \in_{0}} \int \frac{λ d y}{z^{2}} cos θ$ ...(1)
चित्र से, $z = r sec θ,$ अर्थात $z^{2} = r^{2} {sec}^{2} θ, y = r tan θ$ , अवकलन करने पर,
$d y = r {sec}^{2} θ d θ$
समीकरण (1 ) में dy तथा $z^{2}$ के मान रखने पर,
$E_{||} = \frac{1}{4 π \in_{0}} λ \int \frac{r {sin}^{2} θ d θ}{r^{2} {sec}^{2} θ} cos θ = \frac{1}{4 π \in_{0}} \frac{λ}{r} \int cos θ d θ$ ... (2 )
विशेष स्थिति में यदि आवेशित तार की लम्बाई अनंत हो, तो $θ$ के सीमांत मान (limiting values )
$θ_{1} = - \frac{π}{2}$ से, $θ_{2} = + \frac{π}{2}$ होंगे | अतः , समीकरण $(2)$ से, परिणामी विद्युत - क्षेत्र, $E_{||} = \frac{1}{4 π \in_{0}} \frac{λ}{r} \int_{- π / 2}^{+ π / 2} cos θ d θ = \frac{1}{4 π \in_{0}} \frac{λ}{r} {[sin θ]}_{- π / 2}^{π / 2}$
$= \frac{1}{4 π \in_{0}} \frac{λ}{r} [sin \frac{π}{2} - sin (- \frac{π}{2})] = \frac{1}{4 π \in_{0}} \frac{λ}{r} [1 - (- 1)]$
$= \frac{1}{4 π \in_{0}} \frac{2 λ}{r} = \frac{λ}{2 π \in_{0} r}$ .
$∴$ परिणामी विद्युत -क्षेत्र का अभीष्ट मान = $\frac{λ}{2 π \in_{0} r}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

BHARATI BHAWAN-विद्युत-क्षेत्र : गॉस का प्रमेय तथा उसके अनुप्रयोग-उदाहरण

Home
Ask Doubt
Profile