A thermally insulated piston divides a nonconducting container in two compartements, right compartement of 2V,T and 2P, while in the left compartement the respective values are V,T and P. Total moles in total system of both comartments is 5 moles. if piston can slide freely, and in the final equilibrium position, volume of right compartement is xV5 then find the value of x.
The correct Answer is:12
Step by step video, text & image solution for A thermally insulated piston divides a nonconducting container in two compartements, right compartement of 2V, T and 2P, while in the left compartement the respective values are V, T and P. Total moles in total system of both comartments is 5 moles. if piston can slide freely, and in the final equilibrium position, volume of right compartement is (xV)/(5) then find the value of x. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCEChapter:KTG & THERMODYNAMICSExercise:Exercise-2
Explore 1 Video
- KTG & THERMODYNAMICSBook:RESONANCEChapter:KTG & THERMODYNAMICSExercise:PART -I
Explore 15 Videos
- KTG & THERMODYNAMICSBook:RESONANCEChapter:KTG & THERMODYNAMICSExercise:SECTION (J)
Explore 2 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCEChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCEChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 65 Videos
Similar Questions
A diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

The heat that flown from right compartment to left compartment before thermal equilibrium is achieved is
View SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.
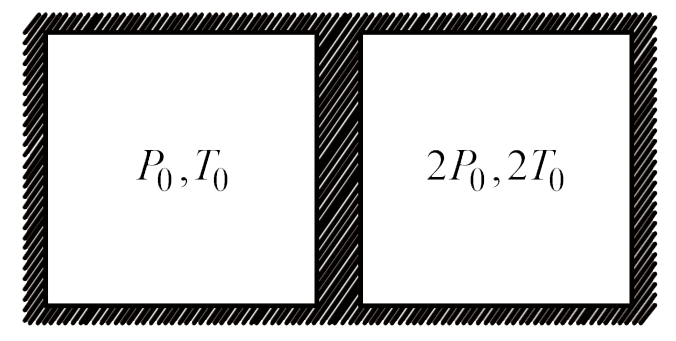
The pressure in left compartment after thermal equilibrium is achieved is
View Solution
Knowledge Check
A partition divides a container having insulated walls into two compartments whose initial paraments are given. The partition is a conducting wall which can move freely without friction. Which of the following statements is/are correct, with refrence to the final equilibrium position ?
 AThe pressure in the two compartments are equal.BVolume of compartment I is 3V/5CVolume of compartment II is 12V/5DFinal pressure in compartment I is 5P/3
AThe pressure in the two compartments are equal.BVolume of compartment I is 3V/5CVolume of compartment II is 12V/5DFinal pressure in compartment I is 5P/3Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of right compartment.AV2(P2T1P2T1+P1T2)BV(P2T1P2T1−P1T2)CV(P2T1P2T1+P1T2)DV(2P2T2P2T1−P1T2)Figure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

Final volume of the left compartment.AV2(P1T2P2T1+P1T2)BV(P1T2P2T1−P1T2)CV(P1T2P2T1+P1T2)DV(2P1T2P2T1+P1T2)
A diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.

If the pin which was keeping the piston fixed is removed and the piston is allowed to slide slowly such that a state of mechanical equilibrium is achieved. The volume of left compartment when piston is in equilibrium is
View SolutionA container is divided into two compartments. One compartment contains 2 moles of N2 gas at 1 atm and 300 K and other compartment contains H2 gas at the same temperature and pressure. Volume of H2 compartment is four times the volume of N2 compartment [Assuming no reaction under these conditions]
Calculate the final total pressure if partition between two compartments is removed.
View SolutionA rigid and insulated tank of 3m3 volume is divided into two compartments. One compartment of volume of 2m3 contains an ideal gas at 0.8314 Mpa and 400 K while the second compartment of volume of 1m3 contains the same gas at 8.314 Mpa and 500 K. If the partition between the two compartments is rptured, the final temperature of the gas is :
View SolutionFigure shows an insulated cylinder of volume V containing monatomic gas in both the compartments. The piston is diathermic. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium. The initial pressures and temperatures are as shown in the figure. Calculate

The final pressures of left and right compartment respectively are
View SolutionIn the figure, a container is shown to have a movable (without friction) piston on top. The container and the piston are all made of perfectly insulated material allowing no heat transfer between outside and inside the container. The container is divided into two compartments by a rigid partition made of a thermally conducting material that allows slow transfer of heat. The lower compartment of the container is filled with 2 moles of an ideal monatomic gas at 700K and the upper compartment is filled with 2 moles of an ideal diatmoic gas at 400K. The heat capacities per mole of an ideal monatomic gas are CV=32R,CP=52R, and those for an ideal diatomic gas are CV=52R,CP=72R,

Now consider the partition to be free to move without friction so that the pressure of gasses in both compartments is the same. The total work done by the gases till the time they achives equilibrium will be
View Solution

