During the expansion process the volume of the gas changes form 4m3 to 6m3 while the pressure change according to p=30V+100 where pressure is in Pa and volume is in m3. The work done by gas in N×102J. Find N.
The correct Answer is:5
To find the work done by the gas during the expansion process, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done by the gas during an expansion or compression is given by the integral of pressure with respect to volume:
W=∫VfViPdV
where Vi is the initial volume and Vf is the final volume.
Step 2: Substitute the Pressure Equation
Given the pressure as a function of volume:
P=30V+100
We can substitute this into the work done formula:
W=∫64(30V+100)dV
Step 3: Break Down the Integral
We can separate the integral into two parts:
W=∫6430VdV+∫64100dV
Step 4: Calculate Each Integral
1. For the first integral:
∫30VdV=30⋅V22=15V2
Evaluating from 4 to 6:
15(62)−15(42)=15(36)−15(16)=540−240=300
2. For the second integral:
∫100dV=100V
Evaluating from 4 to 6:
100(6)−100(4)=600−400=200
Step 5: Combine the Results
Now, add the results of both integrals to find the total work done:
W=300+200=500J
Step 6: Express the Work Done in the Required Format
The problem states that the work done can be expressed as N×102J. We have:
500J=5×102J
Thus, by comparing, we find:
N=5
Final Answer
The value of N is 5.
---
The work done by the gas during an expansion or compression is given by the integral of pressure with respect to volume:
W=∫VfViPdV
where Vi is the initial volume and Vf is the final volume.
Given the pressure as a function of volume:
P=30V+100
We can substitute this into the work done formula:
W=∫64(30V+100)dV
We can separate the integral into two parts:
W=∫6430VdV+∫64100dV
1. For the first integral:
∫30VdV=30⋅V22=15V2
Evaluating from 4 to 6:
15(62)−15(42)=15(36)−15(16)=540−240=300
∫100dV=100V
Evaluating from 4 to 6:
100(6)−100(4)=600−400=200
Now, add the results of both integrals to find the total work done:
W=300+200=500J
The problem states that the work done can be expressed as N×102J. We have:
500J=5×102J
Thus, by comparing, we find:
N=5
The value of N is 5.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - Exercise-2
1 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - PART -I
15 Videos
- KTG & THERMODYNAMICSBOOK - RESONANCECHAPTER - KTG & THERMODYNAMICSEXERCISE - SECTION (J)
2 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBOOK - RESONANCECHAPTER - KINETIC THEORY OF GASES AND THERMODYNAMICSEXERCISE - Exercise
64 Videos
- MAGNETIC FIELD AND FORCESBOOK - RESONANCECHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Exercise
65 Videos
Similar Questions
In an adiabatic process, volume of gas changes from 1200x10−6m3 to 300x10−6m3. Initial pressure of gas is 200 KPa. For the process is γ=1.5. Find work done by gas in the process.
View SolutionPressure and volume of a gas changes from (p0V0) to (p04,2V0) in a process pV2= constant. Find work done by the gas in the given process.
View Solution
Knowledge Check
A gas expands from 2m3 to 2.5m3 at constant pressure 103 pa, the work done is
A50 JB25 JC500 JD250 JThe work done during the expanision of a gas from a volume of 4dm3 to 6dm3 against a constant external pressure of 3 atm is (1 L atm = 101.32 J)
A+304JB−304JC−6JD−608JThe work done during the expanision of a gas from a volume of 4dm3 to 6dm3 against a constant external pressure of 3 atm is (1 L atm = 101.32 J)
A+304JB−304JC−6JD−608J
One mole of an ideal gas is kept enclosed under a light piston (area =10−2m2) connected by a compresses spring (spring constant 100N/m). The volume of gas is 0.83m3 and its temperature is 100K. The gas is heated so that it compresses the spring further by 0.1m. The work done by the gas in the process is N×10−1J. Find N. (Take R=8.3J/K−mole) and suppose there is no atmosphere).
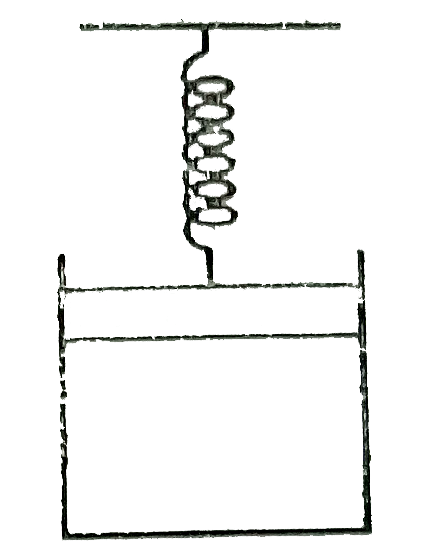
View SolutionThe pressure of a gas is 100 k Pa. if it is compressed from 1 m3 to 10dm3 , find the work done .
View SolutionAt a constant pressure of 20 Pa a gas is compressed from 10 m3 to 5 m3. Later 100 J of heat is added to the system. The change in internal energy is
View SolutionAt a constant pressure of 104Nm−2 , a gas expands by 0.25m3 work done by the gas is
View SolutionThe volume of a gas expands by 0.25m3 at a constant pressure of 103Nm2. The work done is equal to
View Solution
