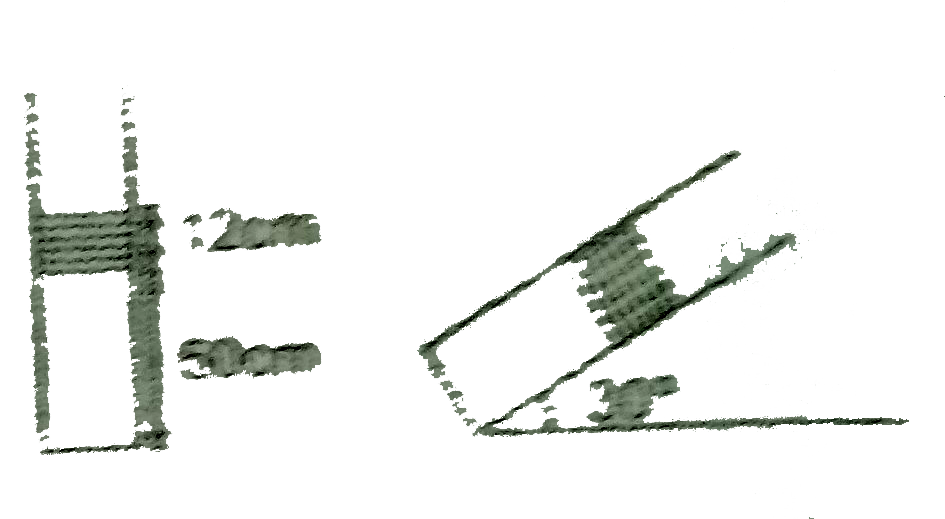
In given figure, an ideal gas is trapped between a mercury column and the closed end of a uniform vertical tube. The upper end of the tube is open to the atmosphere. Initially the lengths of the mercury column and the trapped air colume are 12cm and 50cm respectively. when the tube is titted solwly in a vertical plane through an angle of 30∘ with horizontal then the new length of air colume is x41m. Find x. Assuming the temperature to remains constant. (Patm=76cmofHg)
The correct Answer is:22
Initial pressure of gas Pi=P0+hρg
final pressure of gas P2=P0+hcos60∘ρg
for air column
P1V1=P2V2
⇒(P0+hρg)A×50=(P0+ρghcos60∘)A×x
x=(76+12)50(76+6)=88×5082=220041cm.
Topper's Solved these Questions
- KTG & THERMODYNAMICSBook:RESONANCEChapter:KTG & THERMODYNAMICSExercise:Exercise-2
Explore 1 Video
- KTG & THERMODYNAMICSBook:RESONANCEChapter:KTG & THERMODYNAMICSExercise:PART -I
Explore 15 Videos
- KTG & THERMODYNAMICSBook:RESONANCEChapter:KTG & THERMODYNAMICSExercise:SECTION (J)
Explore 2 Videos
- KINETIC THEORY OF GASES AND THERMODYNAMICSBook:RESONANCEChapter:KINETIC THEORY OF GASES AND THERMODYNAMICSExercise:Exercise
Explore 64 Videos
- MAGNETIC FIELD AND FORCESBook:RESONANCEChapter:MAGNETIC FIELD AND FORCESExercise:Exercise
Explore 65 Videos
Similar Questions
An ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View Solution
Knowledge Check
A mercury barometer reads 75cm in vertical position . If the tube is inclined by 60∘ to the vertical, the length of the mercury in the tube will be
A37.5 cmB75cmC112.5cmD150cmWhat will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDx
What will be the length of mercury column in a barometer tube, when the atmospheric pressure is 76 cm of mercury and the tube is inclined at an angle of 30∘ with the horizontal direction ?
View SolutionWhat will be the length of mercury column in a barometer tube when the atmosperic pressure is 75cm of mercury and the tube is inclined at an angle of 60∘ with the horizontal direction?
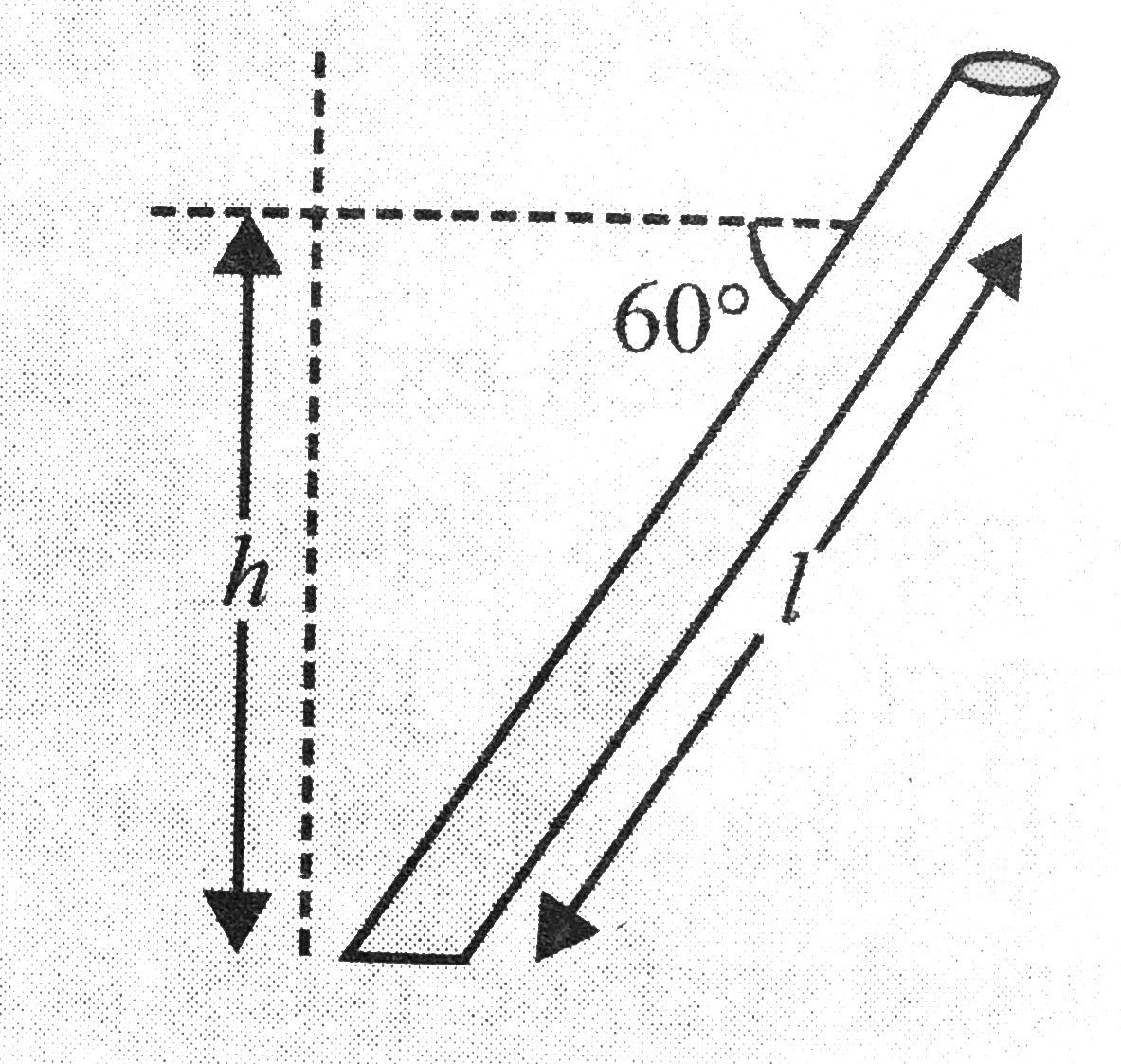
View SolutionA barometer tube is inclined at an angle of 30∘ with horizontal direction. Calculate length of mercury column in tube if atmospheric pressure is 76 cm of mercury.
View Solution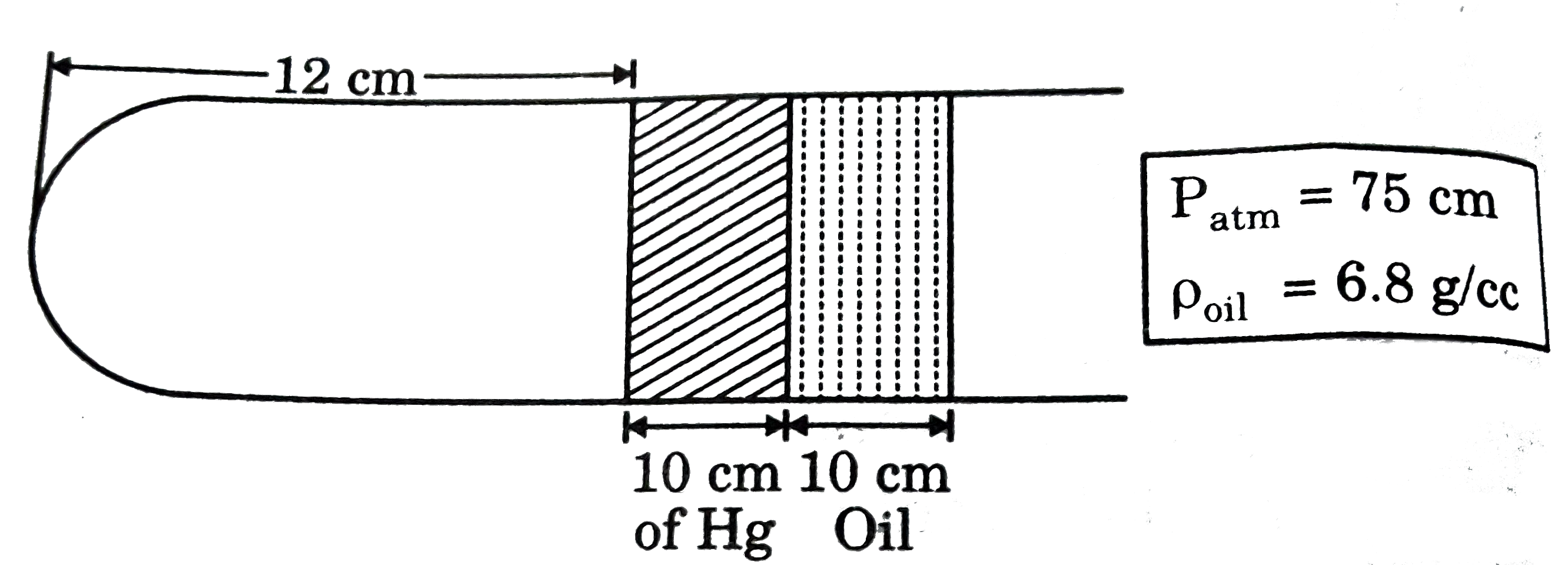
If above tube is held vertical with open end upward then find the length of air column (in cm).
View Solution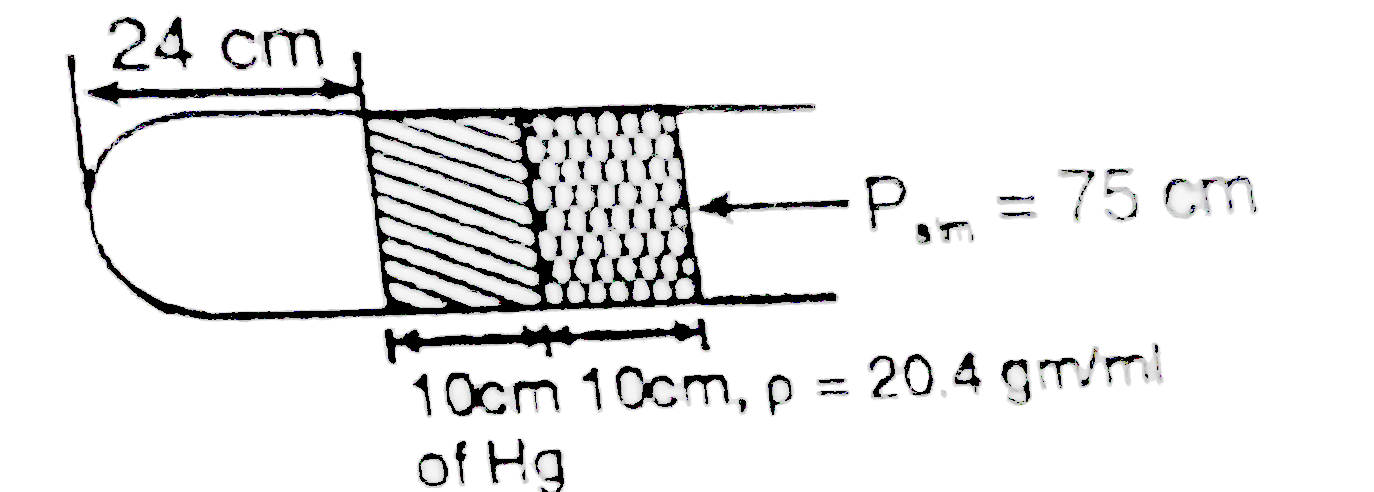
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionIn given figure, A uniform cylindrical tube closed at one end, contains a pallet of mercury 5cm long. When the tube is kept verticaly with the closed end downward, the length of the air column trapped is 30cm. Now the tube is inverted so that the closed end goes up find the new length of the air column trapped. atmospheric pressure =75cm of mercury. (Assume temperature remains constant in this process)

View Solution