Consider a block of mass 'm' attached to a spring of spring constant 'K' as shown. Now a block of same mass 'm' moving with velocity 'u' strikes the other block and stick to it. Both blocks collectively start performing SHM.
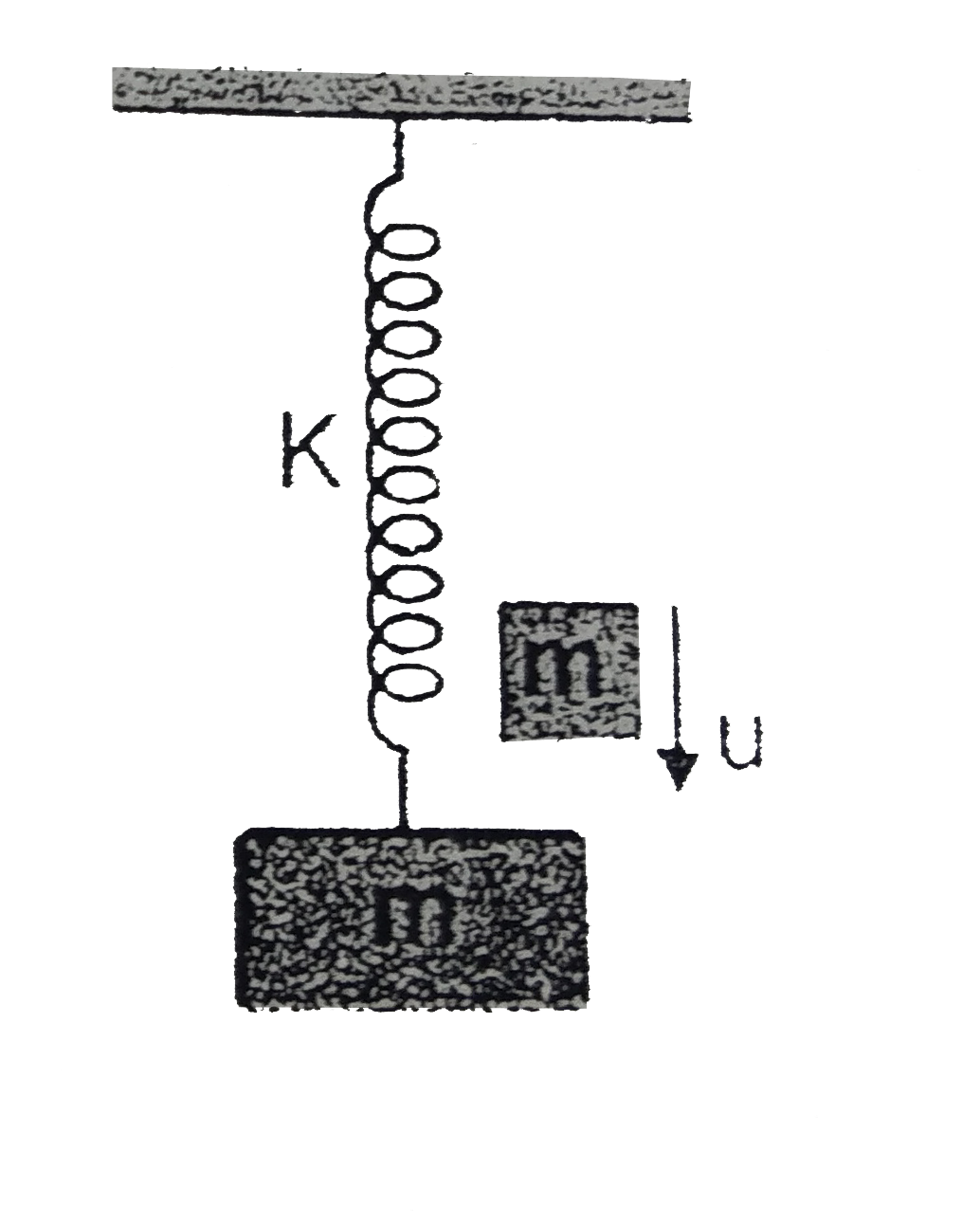
Choose the correct option(s) :
The maximum extension in the spring is 2mgK+A (Where 'A' is amplitude)
The maximum extension in the spring is 2mgK (Where 'A' is amplitude)
The velocity of the block at the instant is at maximum extension is zero.
The maximum extension in the spring is 2mgK+2A (Where 'A' is amplitude)
The correct Answer is:A, C
xmax=2mgK+A
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:Physics
Explore 775 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PT-01
Explore 30 Videos
- TEST PAPERSBook:RESONANCEChapter:TEST PAPERSExercise:PART - II PHYSICS SEC - 2
Explore 20 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCEChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCEChapter:TEST SERIESExercise:PHYSICS
Explore 127 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionIn the figure shown, a block A of mass m is rigidy attached to a light spring of stiffness k and suspended from a fixed support. Another block B of same mass is just placed on it and blocks are in equilibrium. Suddenly the block B is removed. Choose the correct options (s) afterward.
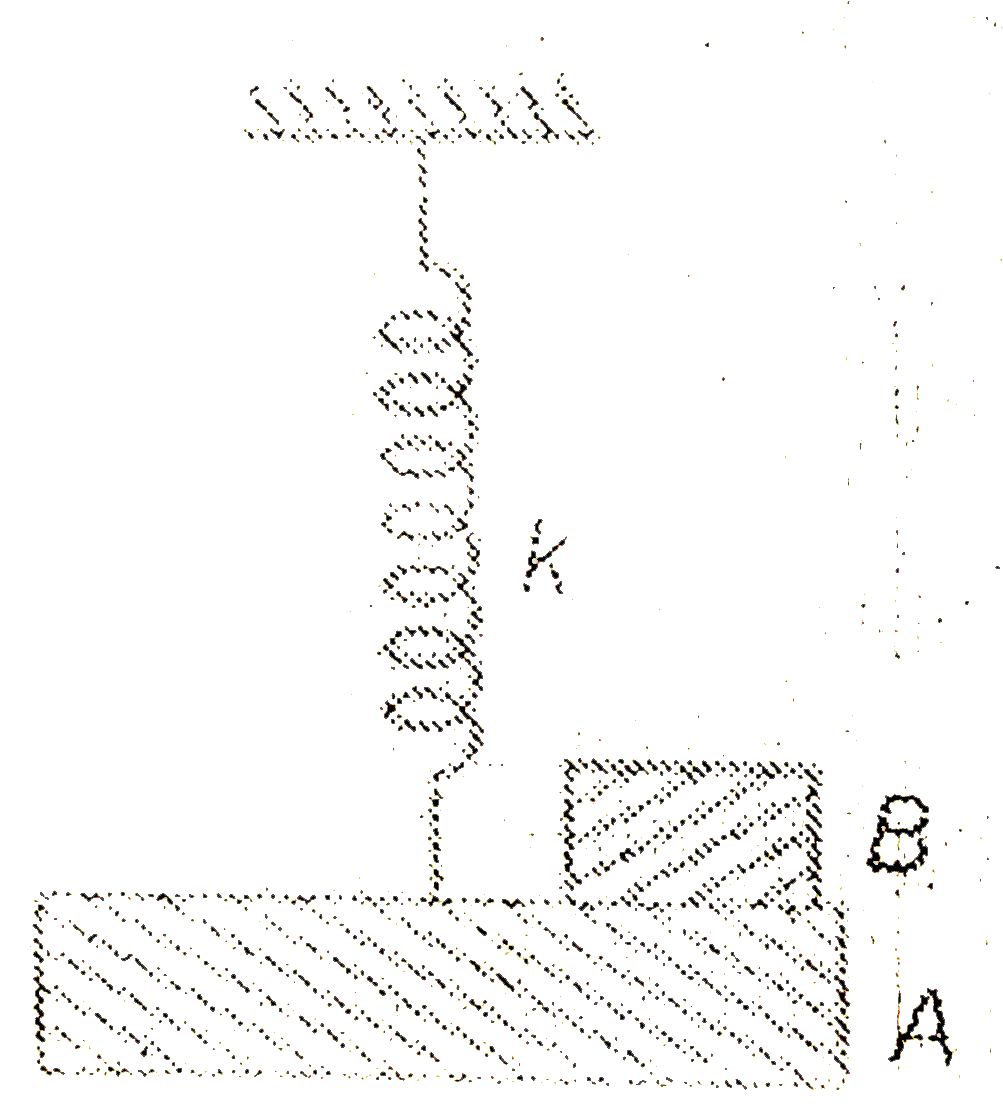
View Solution
Knowledge Check
Consider a block of mass 'm' attached to a spring of spring constant 'K' as shown. Now a block of same mass 'm' moving with velocity 'u' strikes the other block and stick to it. Both blocks collectively start performing SHM.

The amplitude (A) of their SHM isAmgKB2mgKC√mμ22K+m2g2K2D√mμ22K−m2g2K2A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kCalculate the period of oscillations of block of mass m attached with a set of springs as shown
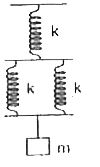 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A block of mass 'm' is hanging from a massless spring of spring constant K. It is in equilibrium under the influence of gravitational force. Another particle of same mass 'm' moving upwards with velocity ao hits the block and sticks to it. For the subsequent motion, choose the incorrect statements:

View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA block of mass m moving with a velocity v0 collides with a stationary block of mass M to which a spring of stiffness k is attached, as shown in Fig. Choose the correct alternative(s)
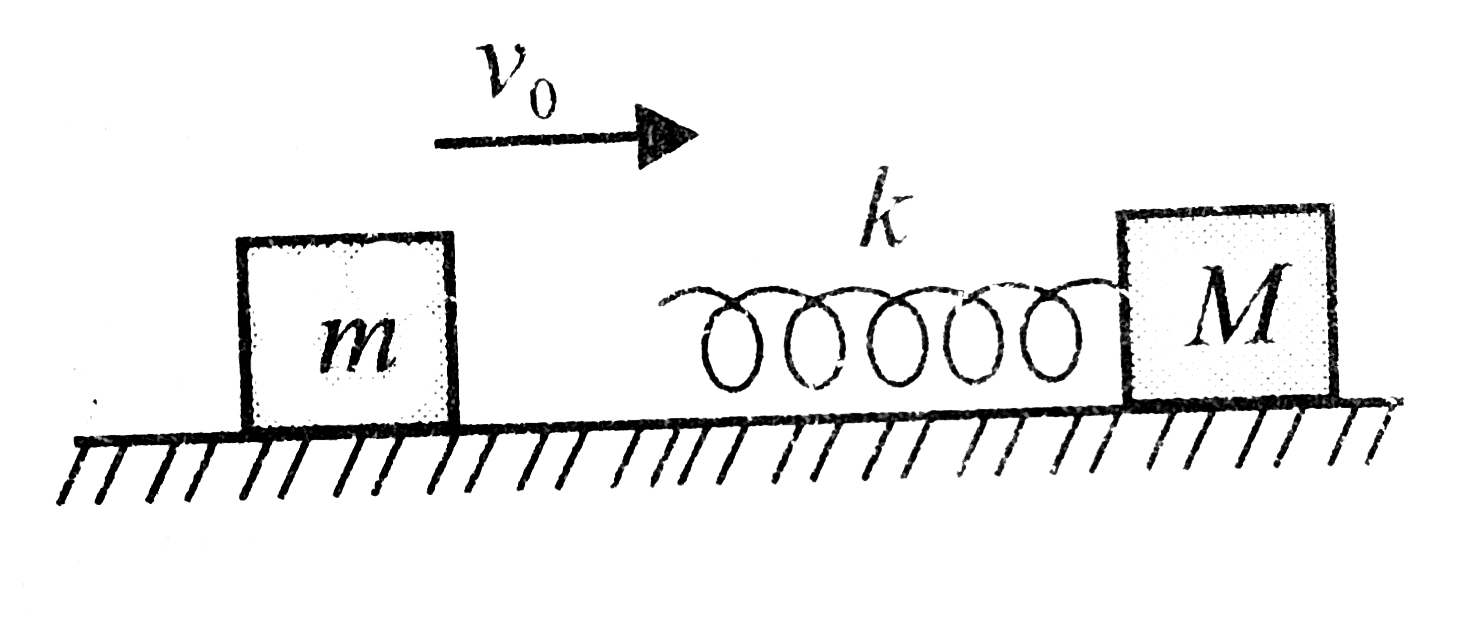
View Solution
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will be
View SolutionA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

View Solution

