A uniform sphere of mass m is positioned between two horizontal planks A and B of mass 2m and m respectively as shown. Ground surface is smooth and friction between planks and sphere is sufficient so that no slipping takes place. Horizontal forces F1 and F2 are applied on plank so that acceleration of sphere is zero. Plank B is moving toward right with acceleration a. Which of the following is/are correct ?

Both planks have same acceleration
Net force sphere is non-zero
F1+F2=175ma
f=5ma
The correct Answer is:C
A uniform ……………..
Since sphere is at rest both friction at top and bottom will be equal as acceleration of sphere is zero. Acceleration of both planks
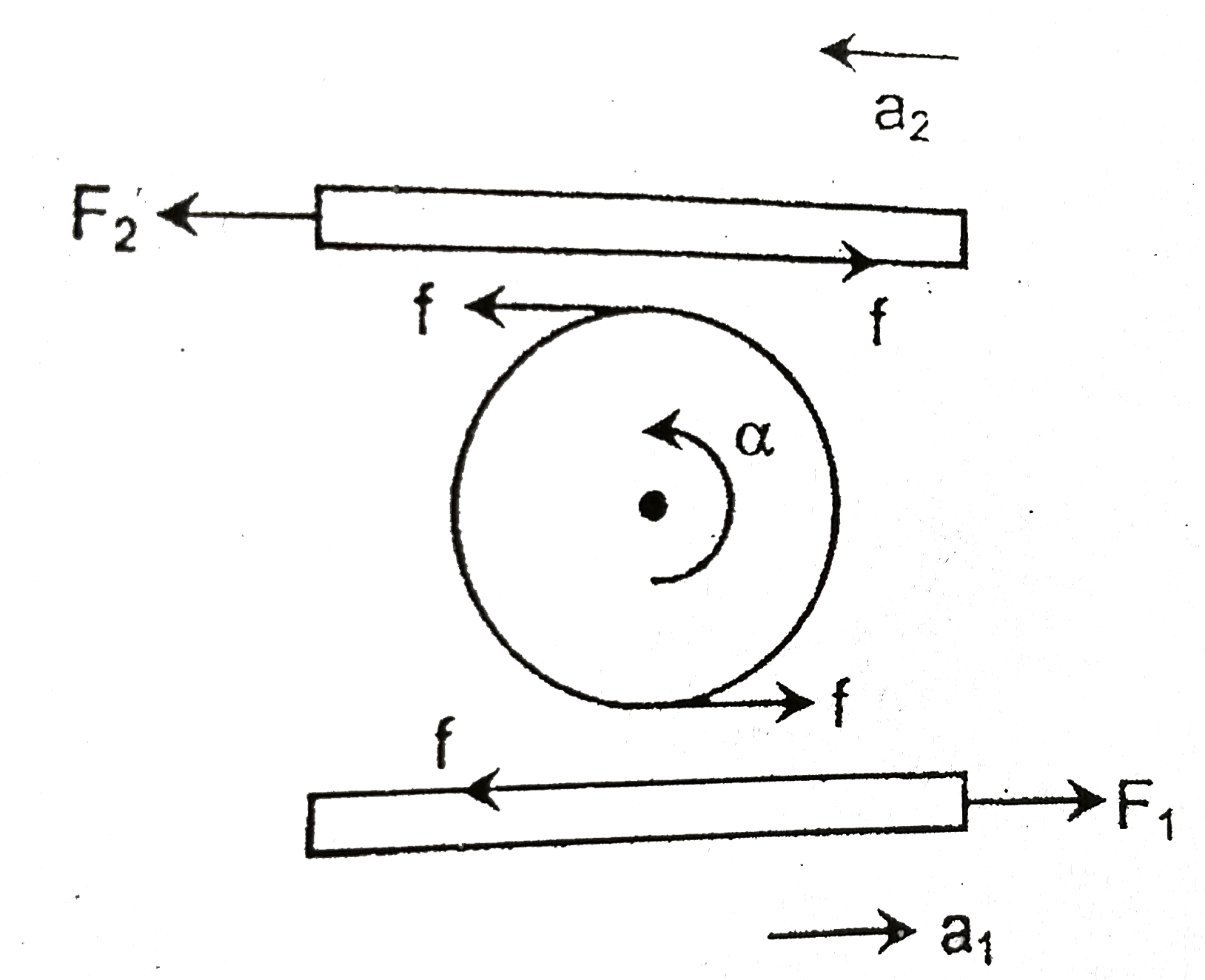
a1=a2=αR=a ∴ No slipping
F1−f=ma ......(1)
F2−f=2ma .......(2)
2fR=25mR2α
⇒2fR=25ma
adding equation (1), (2) and (3)
E1+F2=(3+25)ma=175ma
x=7
Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View Solution
A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
View Solution
Knowledge Check
A uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,
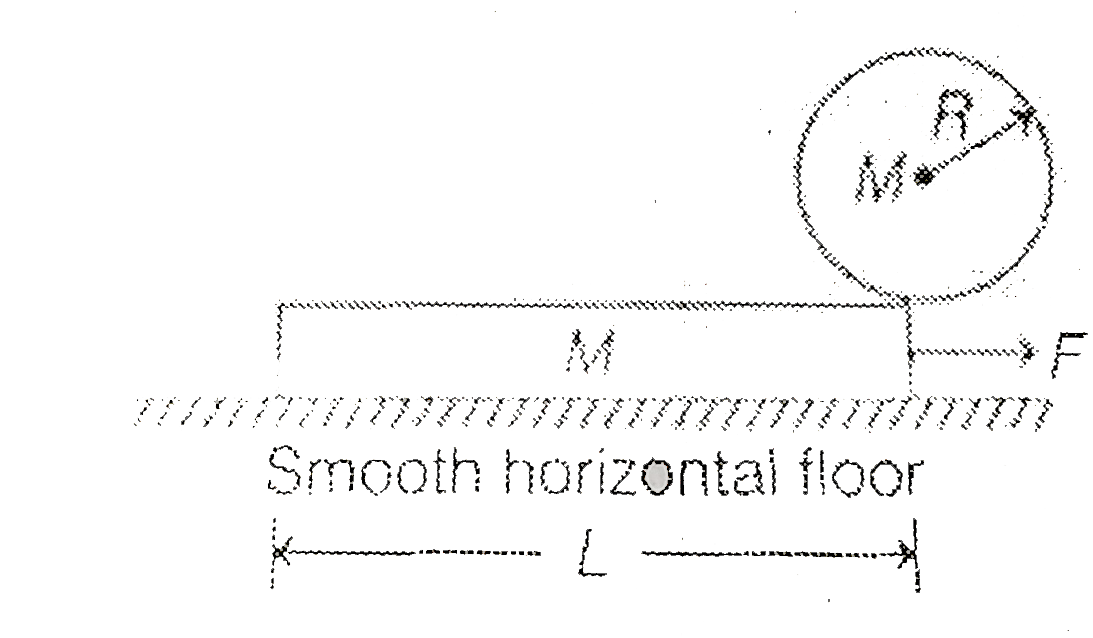
The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The magnitude of acceleration of plank isAF6MBF4MC3F2MD3F4MA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,

The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The magnitude of angular acceleration of the disc isAF4MRBF8MRCF2MRD3F2MRIn Fig a sphere of radius 2m rolls on a plank. The accelerations of the sphere and the plank are indicated. The value of α is
 A2rad/s2B4rad/s2C3rad/s2D1rad/s2
A2rad/s2B4rad/s2C3rad/s2D1rad/s2
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
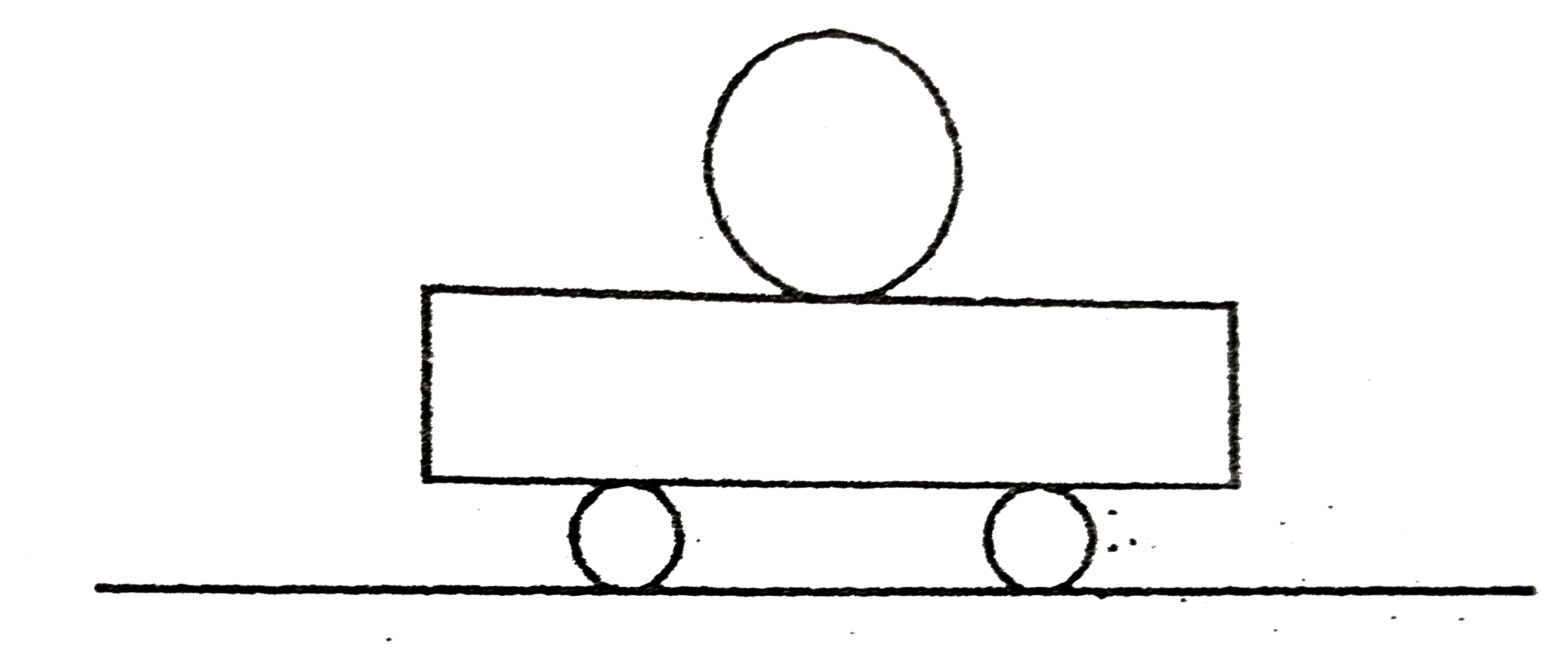
Angular acceleration of sphere is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
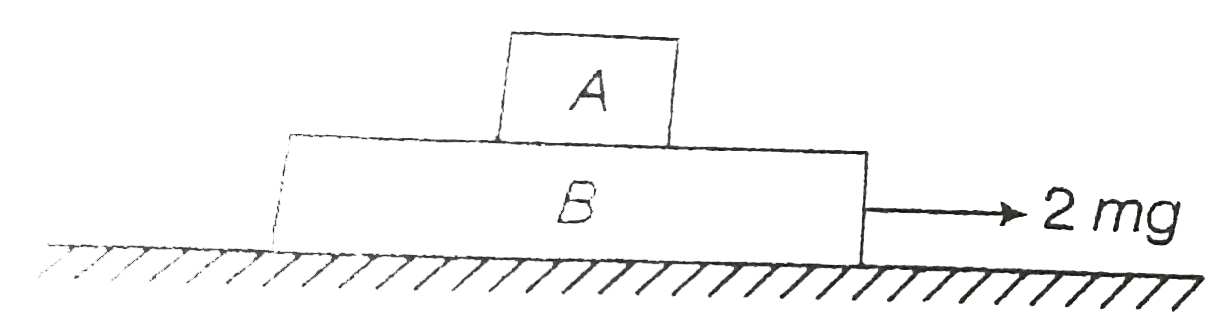
View SolutionBlock of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are
View SolutionA uniform disc of mass M and radius R initially stands vertically on the right end of a horizontal plank of mass M and length L, as shown,
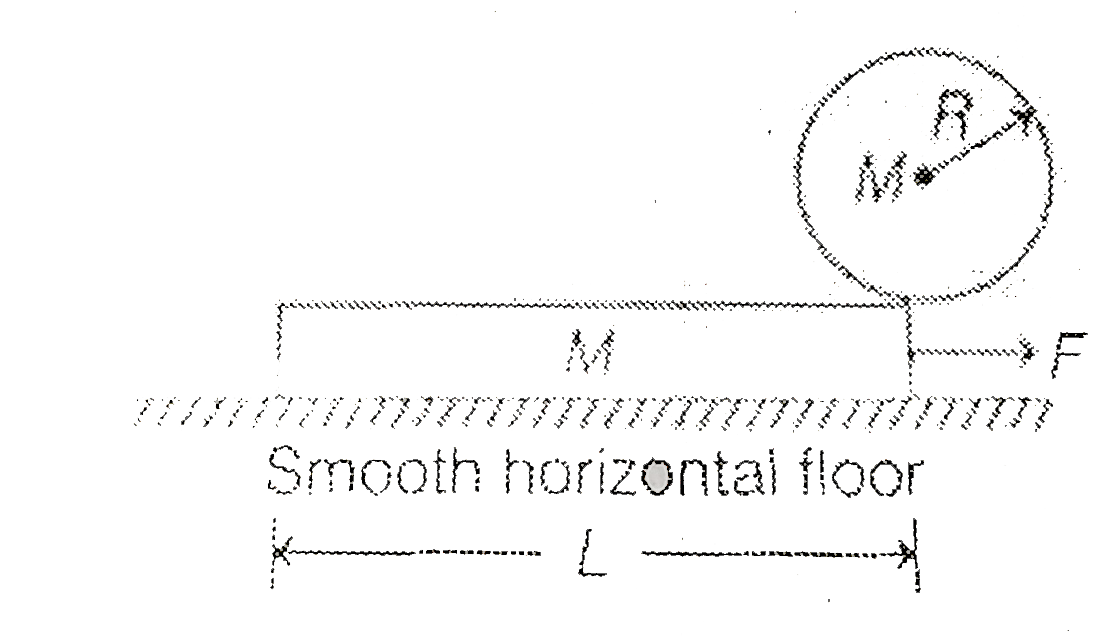
The plank rests on a smooth horizontal floor and friction between disc and plank is sufficiently high such that disc rolls on plank without slipping . The plank is pulled to right with a constant horizontal force of magnitude F.
The distance travelled by centre of disc from its initial position till the left end of plank comes vertically below the centre of disc is
View Solution
