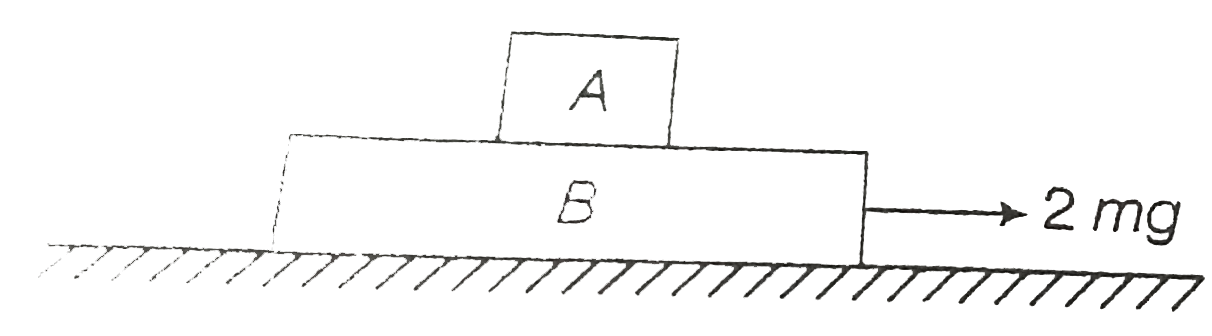
Block of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are
0,(g),(2)
0,2g3
3g5,g5
2g5,g5
The correct Answer is:D
(d) Block A moves due to friction. Maximum value of friction can be μmAg. Therefore, maximum acceleration of A can be μmgma or μg=0.2g=g5. When force 2 mg is applied on lower block, common acceleration (if both move together) will be,
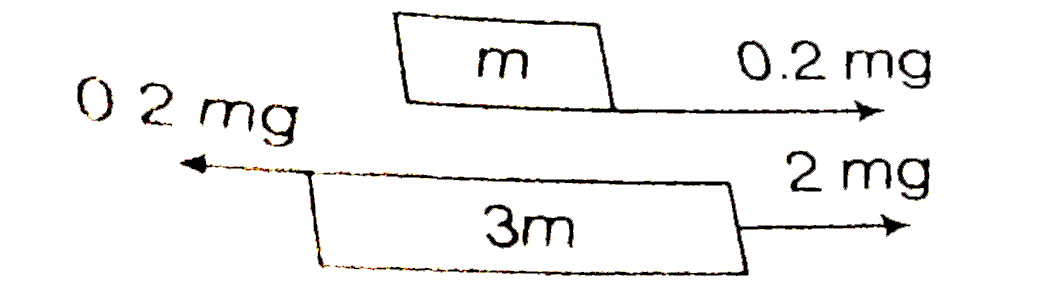
a=Net forceTotal mass=2mg4m=g2
Since a =g/2 is greater than maximum acceleration of A which can be give to it by friction. Therefore slipping will take place.
aA=0.2g=g5
aB=2mg−0.2mg3m=0.6g=3g5
aAB=aA−aB=+(g5−3g5)
=−2g5(in backward direction)
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Assertion and reason
Explore 28 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Match the columns
Explore 7 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Check point 5.4
Explore 20 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
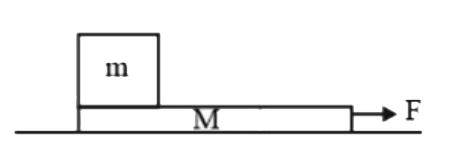
A block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is μ=13. If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together

View SolutionA block A of mass m is placed over a plankB of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v0 toward right Find acceleration (in ms−2 of B relative to A
View Solution
Knowledge Check
A block of mass m =2 kg is placed on a plank of mass M = 10 kg, which is placed on a smooth horizontal plane as shown in the figure. The coefficient of friction between the block and the plank is μ=13. If a horizontal force F is applied on the plank, then the maximum value of F for which the block and the plank move together is (g=10m/s2)
 A50 NB40 NC120 ND100 N
A50 NB40 NC120 ND100 NA block A of mass m is over a plank B of mass 2m. Plank B si placed over a smooth horizontal surface. The coefficient of friction between A and B is 12. Blocks A is given a velocity V0 towards right. Then
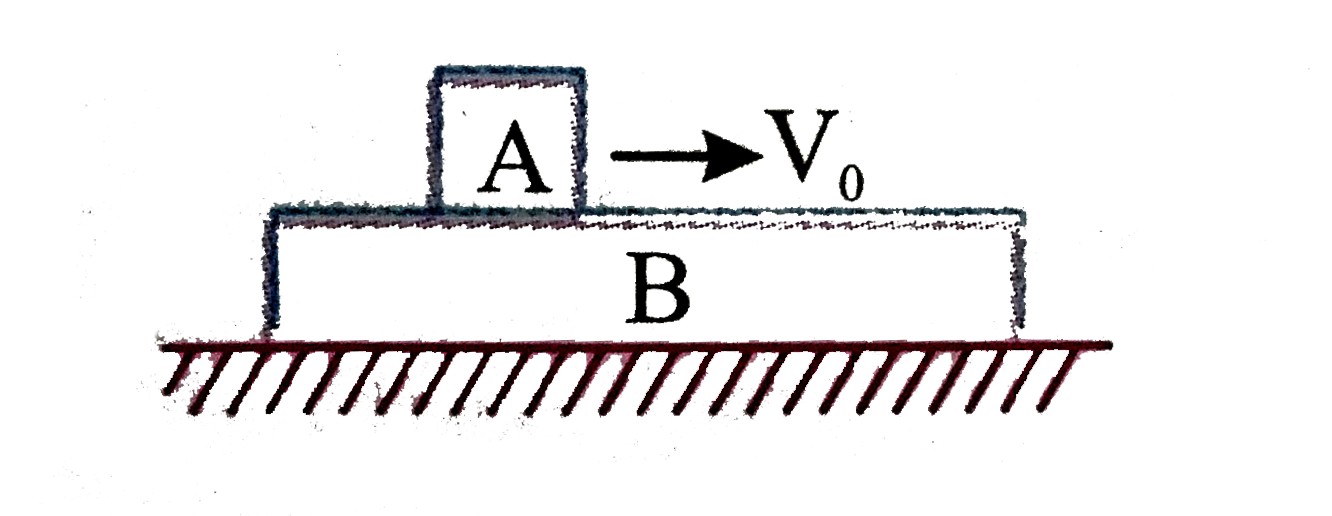 AAcceleration of A is g2BAcceleration of A is gCAcceleration of B relative to A is 34gDAcceleration of A is zero
AAcceleration of A is g2BAcceleration of A is gCAcceleration of B relative to A is 34gDAcceleration of A is zeroA bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :
 Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionA plank of mass 3m is placed on a rough inclined plane and a man of mass m, the coefficient of friction between the board and inclined plane is μ=0.5, the minimum acceleration of man so that plank does not slide is :

View SolutionA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
View SolutionA block of mass 2 kg rests on a rough horizontal plank , the coefficient of friction between the plank and block is 0.3. If the plank is pulled horizontally with a constant acceleration of 4m/s2 , the distance moved by the block on the plank in 5 second starting from rest (in m) is : (Take g = 10m/s2)
View Solution