Consider a spring that exerts the following restoring force :
F=−kx for x≥0
F=−4kx for x<0
A mass m on a frictionless surface is attached to the spring displaced to x=A by strectching the spring and released :
The period of motion will be T=32π√mk
The most negative value of x the mass m can reach will be x=−A2
The time taken to move from x=A to x=+A√2 , straight away will be equal to 5π8√mk
The total energy of oscillations will be 52kA2
The correct Answer is:A, B
Consider a ………….
T=12(2π√mk+2π√m4k)
T=32π√mk
12kA2=124kA2⇒A'A2 .
Similar Questions
The force constant between the restoring force F and displacement x of a spring accoring to the graph shown will be
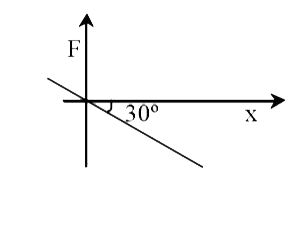
View SolutionOn compressing a spring by 0.5 m, a restoring force of 20 N is developed. When a body of mass 5 kg is placed on the spring, then calculate the (a) force constant of the spring.
(b) the distance through which the spring is depressed under the weight of the body.
(c ) the period of oscillation of the spring if the the body is pushed down and then released.
View Solution
Knowledge Check
In SHM restoring force is F=−kx, where k is force constant, x is displacement and a is amplitude of motion, then total energy depends upon
Ak,a and mBk,x,mCk,aDk,x
Figure. (a) shows a spring of force constant k fixed at one end and carrying a mass m at the other end placed on a horizontal frictionless surface. The spring is stretched by a force F. Figure. (b) shows the same spring with both endsf free and a mass m fixed at each free end Each of the spring is streched by the same force F. The mass in case (a) and the masses in case (b) are then released. Which of the following statements are true?AWhile oscillating the maximum extension of the spring is more in case (a) than in case (b).BThe maximum extension of the spring is same in both cases.CThe time period of oscillation is the same in both cases.DThe time period of oscillation in case (a) is √2 time that in case (b).The left and of the spring tied to a wall and at the right end is attached to a block of mass m, which is placed on a frictionless ground. The force F displaces the block by distance x where it is exactly balanced by the spring force.

What is the maximum speed of the block in the ensuing motion after the force F is removed?A√FxmB√Fx2mC√2FxmDx√Fm
In Fig. three identical massless springs are kept horizontal. The left end of the first is tied to a wall. The left end of the second spring is tied to a block of mass m placed on rough ground and the ,eft end of the third spring is tied to a block of mass m placed frictionless ground. The right end of each spring is pulled by a force that is increased gradually from zero to F. Extensions in these springs are x1, x2 and x3, respectively. Find the relationship between x1, x2, and x3

View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the displacement function x(t) for the spring block system?
View SolutionIn the figure shown the spring is compressed by 'x0' and released . Two block 'A' and 'B' of masses 'm' and '2m' respectively are attached at the ends of the spring. Blocks are kept on a smooth horizontal surface and released. Find the work done by the spring on 'A' by the time compression of the spring reduced to x02.

View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View SolutionA pendulum makes perfectly elastic collision with block of m lying on a frictionless surface attached to a spring of force constant k. Pendulum is slightly displaced and released. Time period of oscillation of the system is
View Solution