The spring force is given by F=−kx, here k is a constant and x is the deformation of spring. The F−x graph is
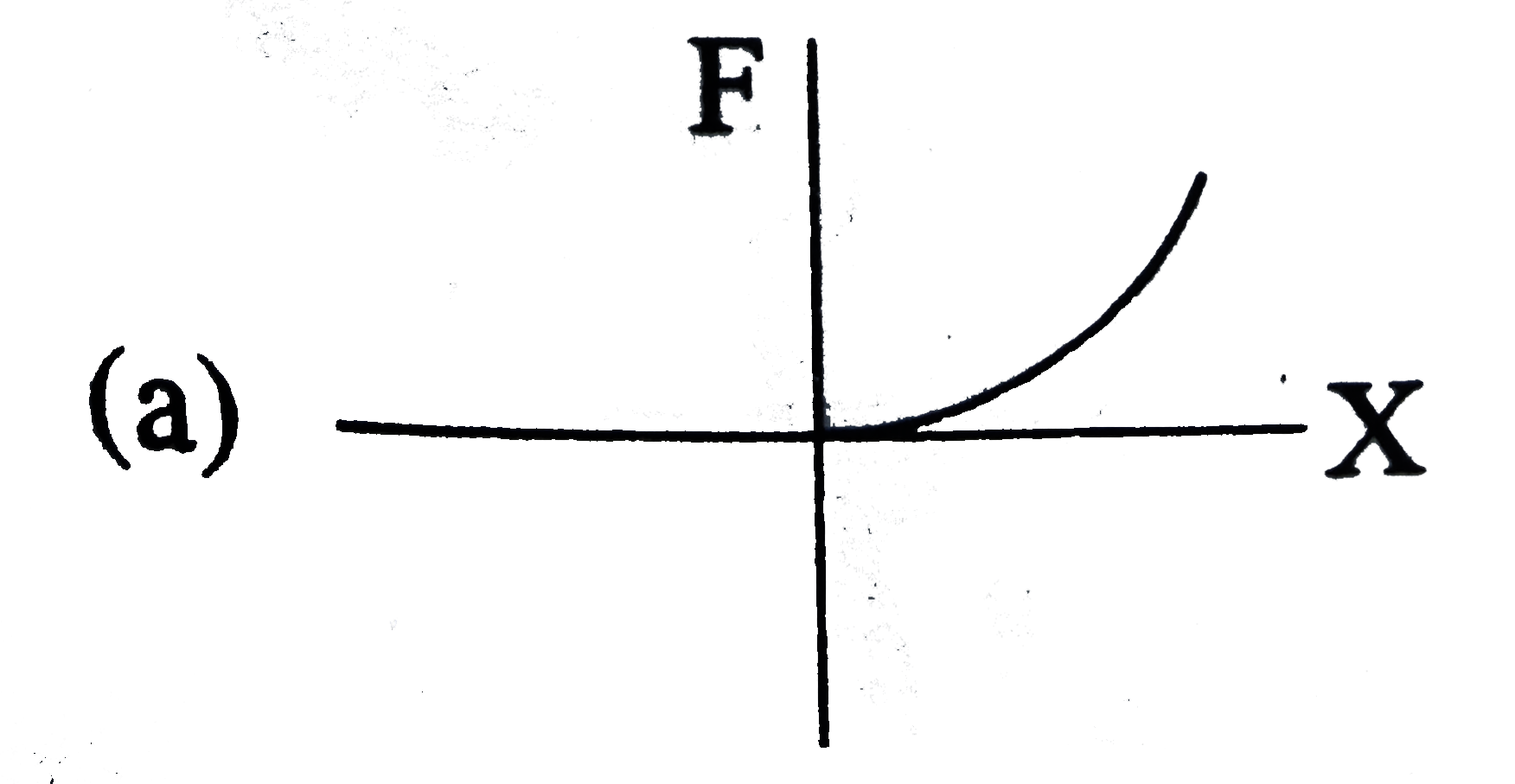


The correct Answer is:C
given F=−10x
The standard equation of straight line is y=mx+c
If we compare given equation with the standard equation of Straight line, the intercapt is zero and slope is negative. Hence the graph is passing through origin.
Hence, option (c ) is correct.
Topper's Solved these Questions
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Fill in the blanks type
Explore 26 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Comprehension Type
Explore 31 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICSChapter:CENGAGE PHYSICS DPPExercise:Multiple Correct Answer Type
Explore 54 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICSChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONBook:CENGAGE PHYSICSChapter:CENTRE OF MASS CONVERSATION OF MOMENTUM AND COLLISIONExercise:Question Bank
Explore 38 Videos
Similar Questions
Define force constant of spring .
View SolutionAn external unknown horizontal force F pulls a smooth block of mass m attached with an ideal spring of stiffness k. Block is initially at rest and spring is relaxed. Find the work done (in J) by the force F, when the block moves with a velocity v and the deformation of the spring is x (k = 25 N/m, v = 1 m/s, m = 1 kg, x =20 cm)
View Solution
Knowledge Check
In SHM restoring force is F=−kx, where k is force constant, x is displacement and a is amplitude of motion, then total energy depends upon
Ak,a and mBk,x,mCk,aDk,xThe restoring force F acting on a particle of mass (m) executing a S. H. M. is given by F= -Kx, where x is the displacement and K is a constant. Then the angular velocity of the particle is given by
A√mKB√KmCmKD√mKThe elastic potential enegry of a stretched spring is given by E=50x2. Where x is the displacement in meter and and E is in joule, then the force constant of the spring is
A50 NmB100Nm−1C100N/m2D100 Nm
Two identical particles each of mass m are connected by a light spring of stiffness K. The initial deformation of the spring when the system was at rest, x0. After releasing the system, if one of the particles has a speed v and the deformation of the spring is x, find the speed of the other particle neglecting friction.
View Solutionspring of force constant k clamped rigidly at onoe end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?

View SolutionA block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
View SolutionA spring of force constant k extends by a length X on loading . If T is the tension in the spring then the energy stored in the spring is
View SolutionA particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
View Solution

