A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)

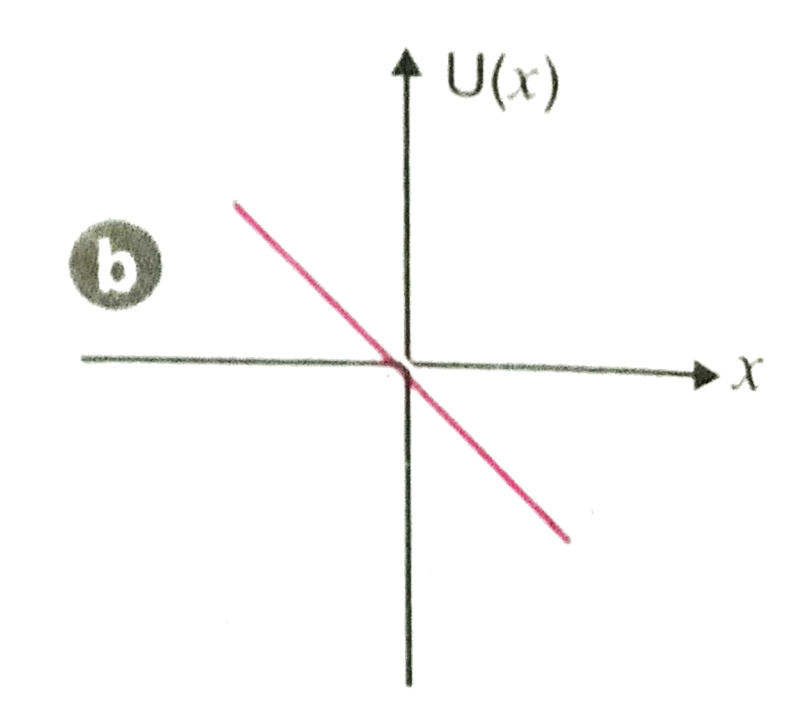
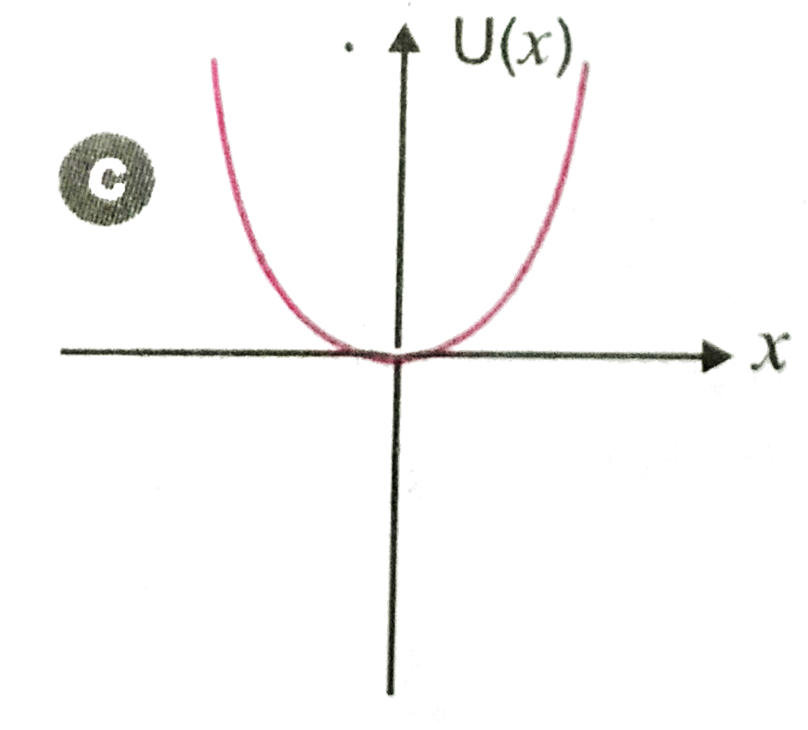
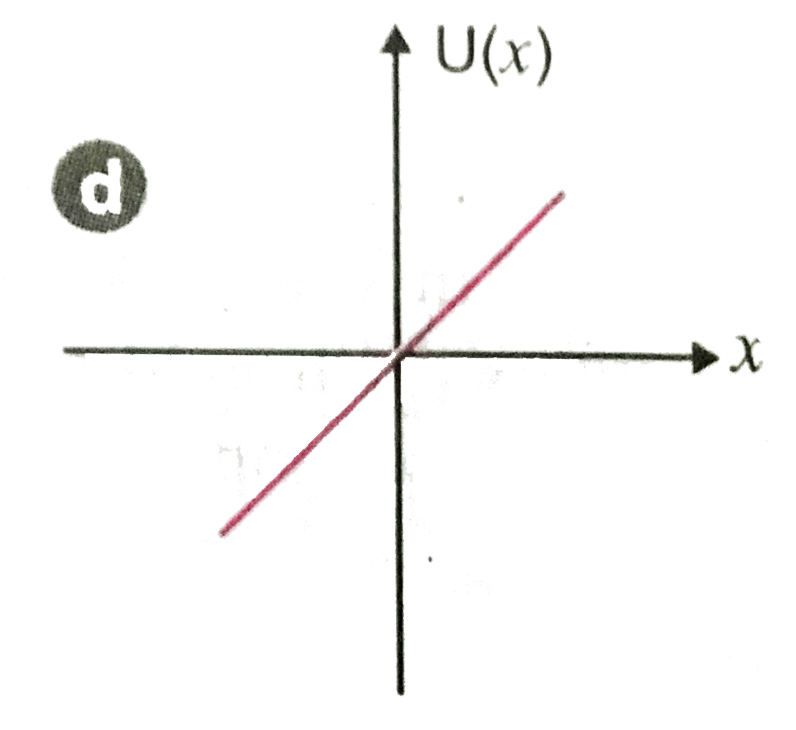
The correct Answer is:A
To solve the problem of finding the potential energy function U(x) given the force F=kx, we can follow these steps:
Step 1: Understand the relationship between force and potential energy
The force acting on a particle is related to the potential energy by the equation:
F=−dUdx
This means that the force is equal to the negative gradient (or derivative) of the potential energy function.
Step 2: Substitute the given force into the equation
We are given that:
F=kx
Substituting this into the relationship gives:
kx=−dUdx
Step 3: Rearrange the equation
Rearranging the equation to isolate dU:
dU=−kxdx
Step 4: Integrate both sides
To find U(x), we need to integrate:
U(x)=−∫kxdx
Calculating the integral:
U(x)=−(k2x2)+C
where C is the constant of integration.
Step 5: Determine the constant of integration
We are given that the potential energy at x=0 is U(0)=0. Substituting x=0 into the equation:
U(0)=−k2(0)2+C=0
This implies that C=0.
Step 6: Write the final expression for potential energy
Thus, the potential energy function is:
U(x)=−k2x2
Step 7: Analyze the graph of U(x)
The function U(x)=−k2x2 represents a downward-opening parabola. The vertex of this parabola is at the origin (0,0), and it decreases as |x| increases.
Conclusion
The graph of U(x) versus x will be a downward-opening parabola.
---
The force acting on a particle is related to the potential energy by the equation:
F=−dUdx
This means that the force is equal to the negative gradient (or derivative) of the potential energy function.
We are given that:
F=kx
Substituting this into the relationship gives:
kx=−dUdx
Rearranging the equation to isolate dU:
dU=−kxdx
To find U(x), we need to integrate:
U(x)=−∫kxdx
Calculating the integral:
U(x)=−(k2x2)+C
where C is the constant of integration.
We are given that the potential energy at x=0 is U(0)=0. Substituting x=0 into the equation:
U(0)=−k2(0)2+C=0
This implies that C=0.
Thus, the potential energy function is:
U(x)=−k2x2
The function U(x)=−k2x2 represents a downward-opening parabola. The vertex of this parabola is at the origin (0,0), and it decreases as |x| increases.
The graph of U(x) versus x will be a downward-opening parabola.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Integer Type Questions
Explore 12 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Asseration - Reason Type Question
Explore 18 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions-II
Explore 14 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
Similar Questions
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a)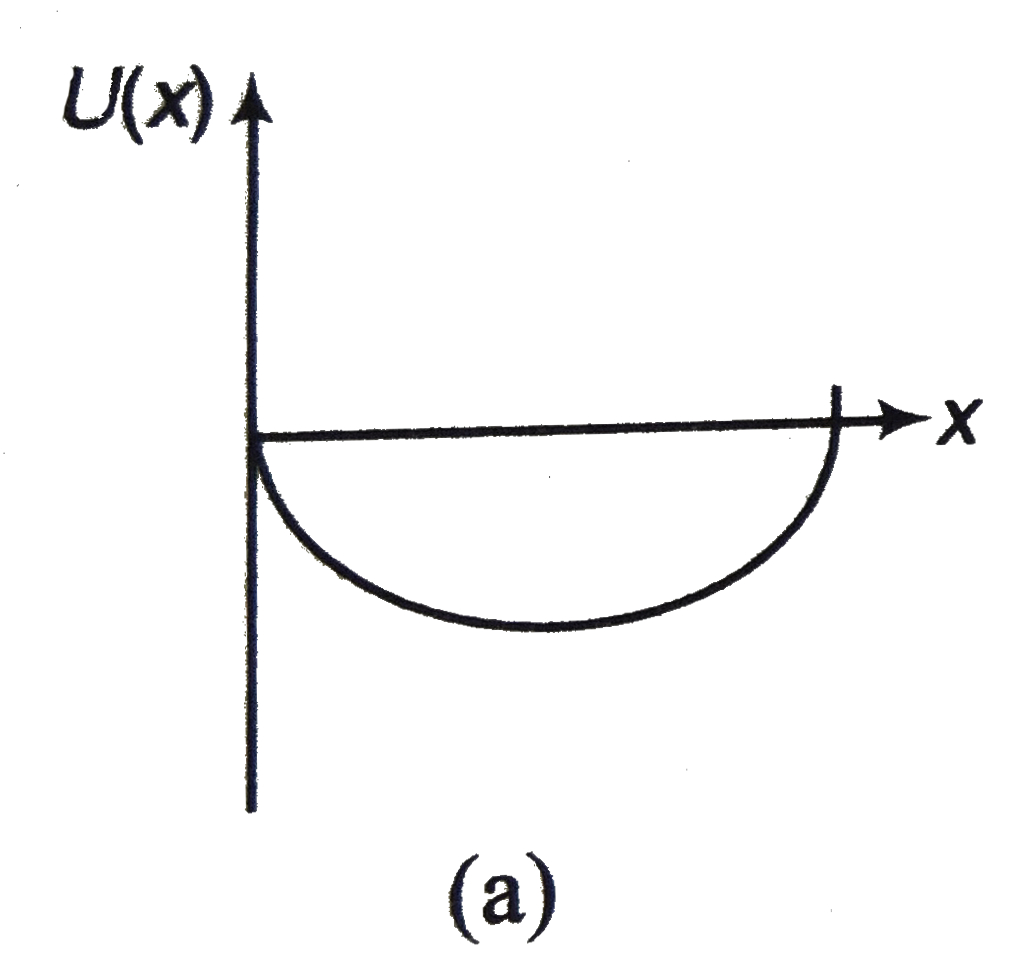 , (b)
, (b) 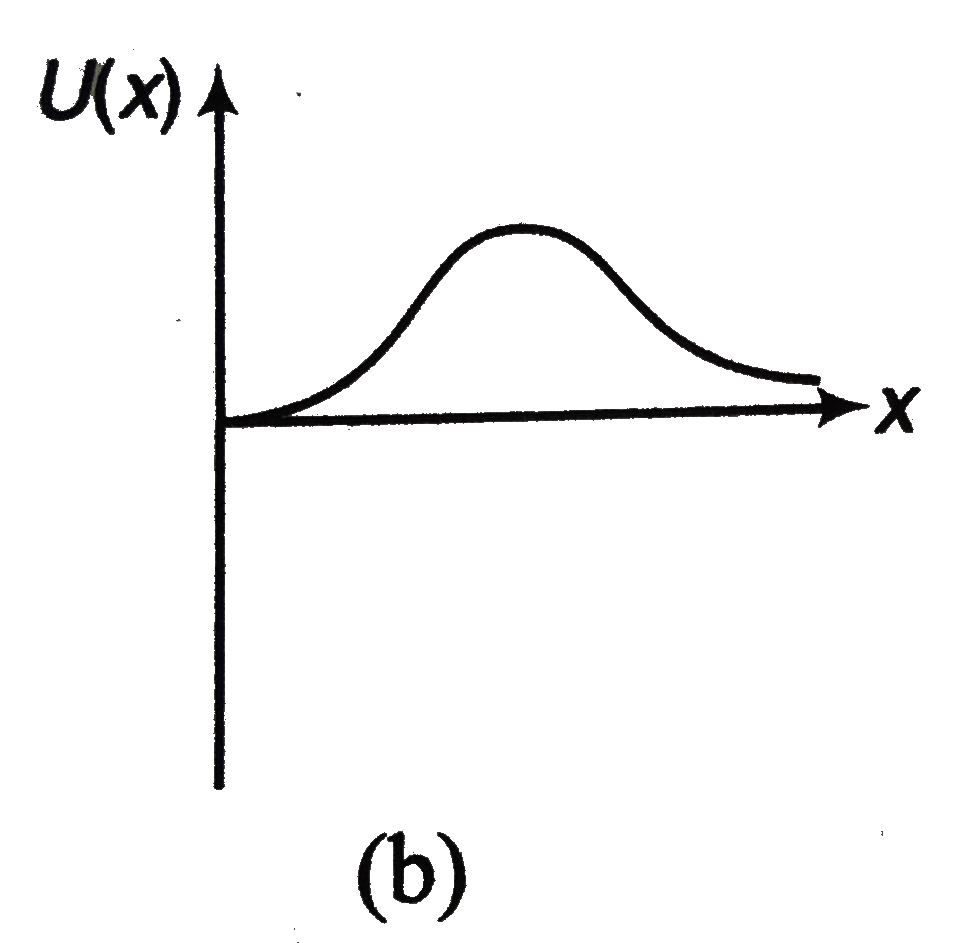 , (c)
, (c) 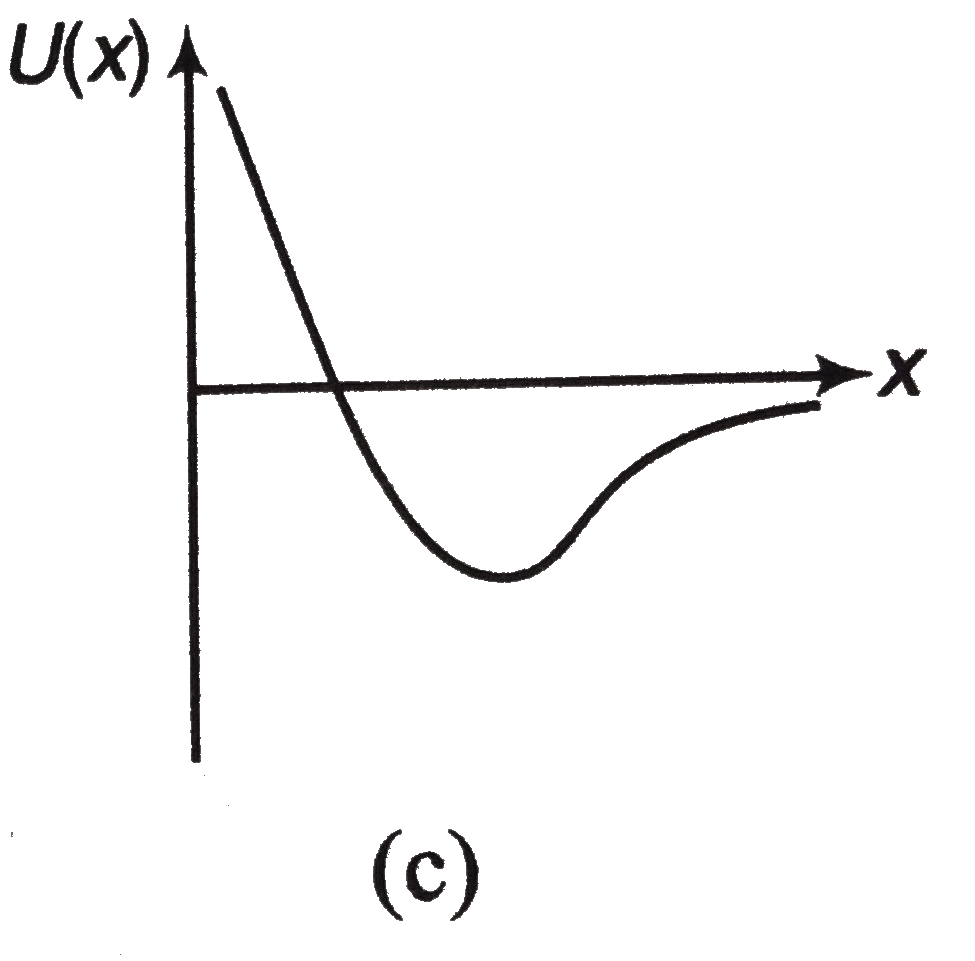 , (d)
, (d) 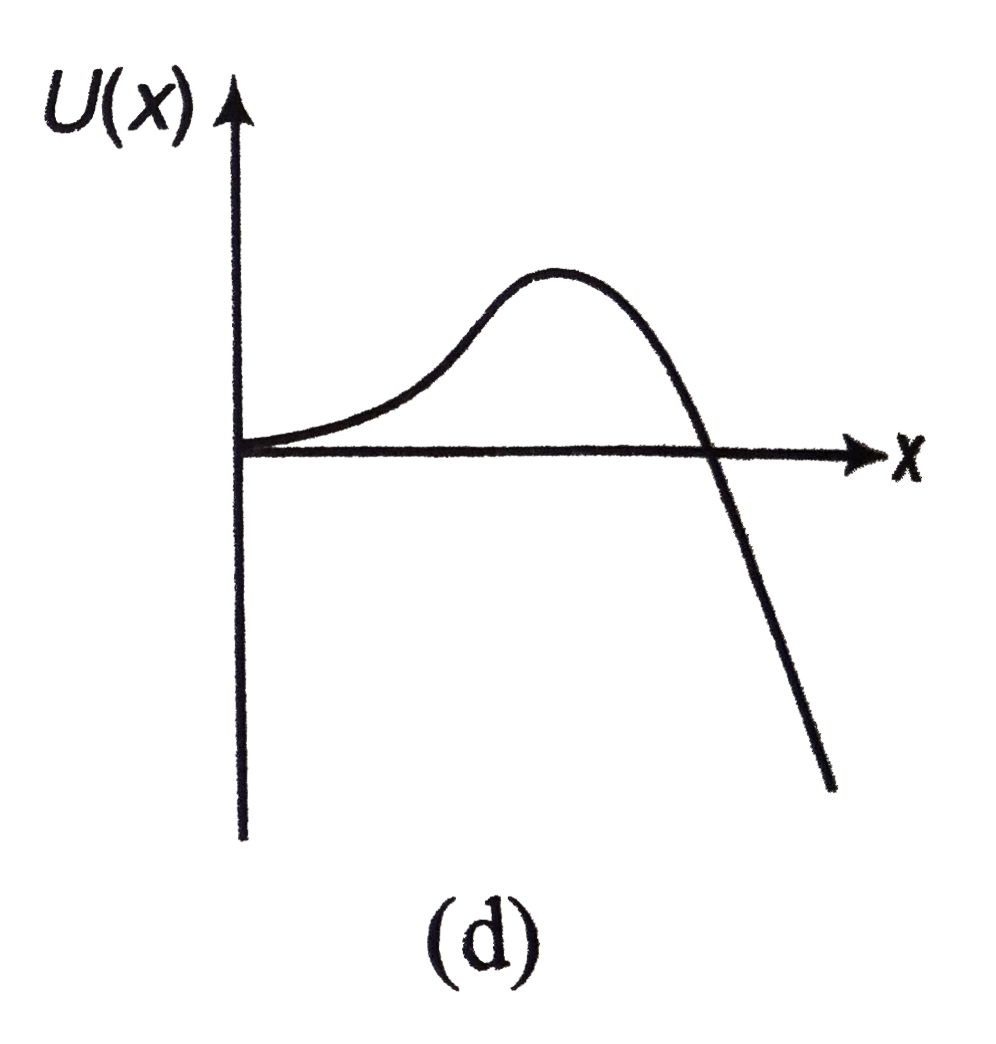 .
.
View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View Solution
Knowledge Check
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
A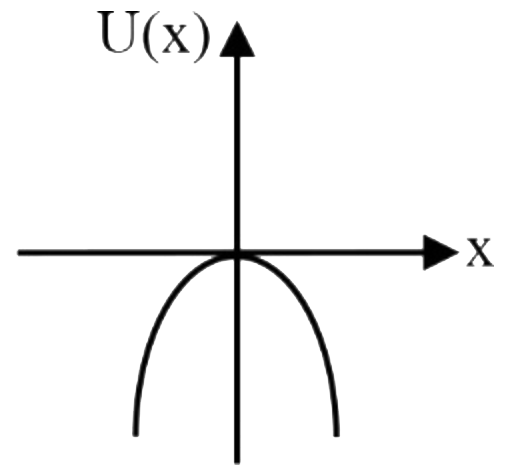 B
B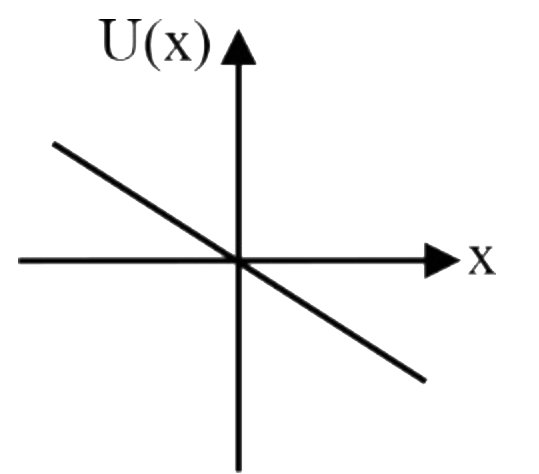 C
C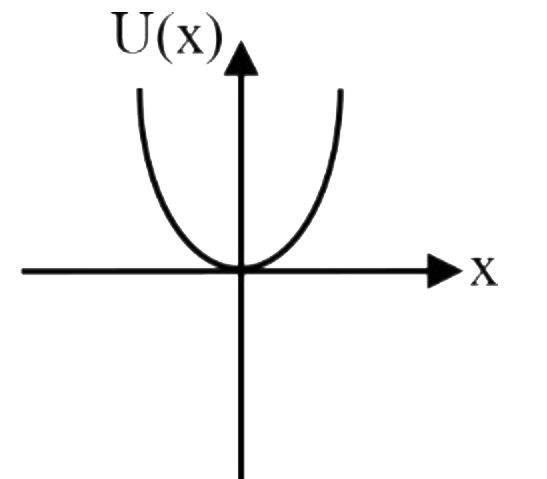 D
D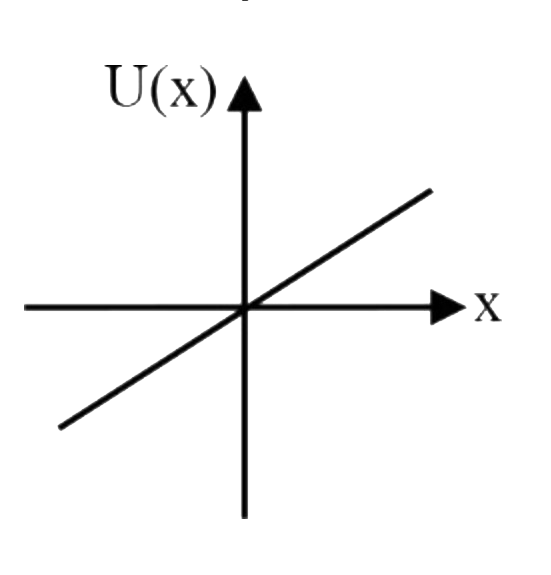
A particle is placed at the origin and a force F=Kx is acting on it (where k is a positive constant). If U(0)=0, the graph of U(x) verses x will be (where U is the potential energy function.)
A B
B C
C D
D
On a particle placed at origin a variable force F=−ax(where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-
A B
B C
C D
D
A particle of mass m is executing osciallations about the origin on the x-axis with amplitude A. its potential energy is given as U(x)=αx4, where α is a positive constant. The x-coordinate of mass where potential energy is one-third the kinetic energy of particle is
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis, it's potential energy is U(x)=k|x|2, where k is a positive constant, if the amplitude of oscillation is a, then it's time period T is
View SolutionThe potential energy U for a force field →F is such that U=−kxy where K is a constant . Then
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View Solution

