A block of mass m rests on a rough horizontal plane having coefficient of kinetic friction μk and coefficient of static friction μs. The spring is in its natural, when a constant force of magnitude P=5μkmg4 starts acting on the block. The spring force F is a function of extension x as F=kx2.( Where k is spring constant )

(a) Comment on the relation between μs and μk for the motion to start.
(b) Find the maximum extension in the spring ( Assume the force P is sufficient make the block move ).
The correct Answer is:(a) 5μK>4μs,(b) x=(μKmgK)1/3
(a) For motion to start
5μkmg4>μsmgor5μk>4μs
(b) , 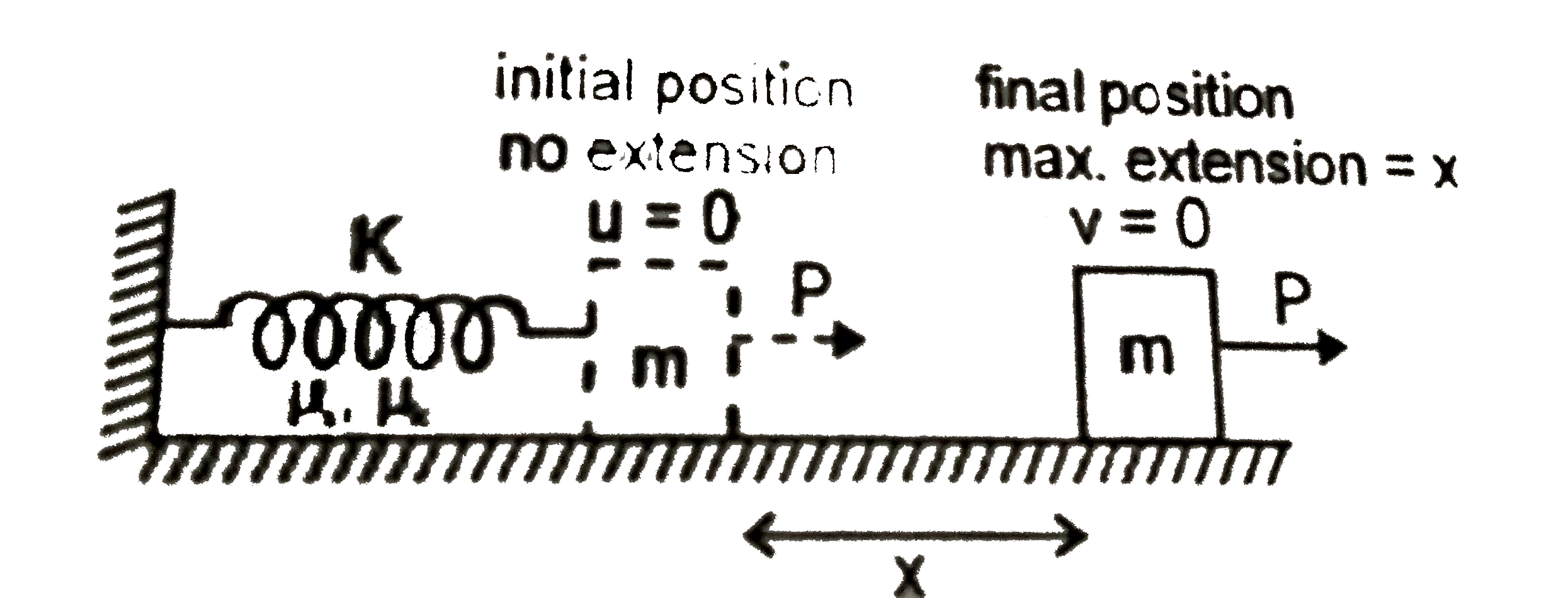
At the final position of block extension in spring is maximum and the sped of the block is v=0 .Hence the net work done in taking the block from initial to final position.
ΔW= work donw by P+ work donw by spring force F+ work done by friction =0
=Px−x∫0Kx3.dx−μmgx=5μkmg4x−Kx44−μkmgx=0
solving we get x=(μKmgK)3/2Ans.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - DPP 50
5 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 51
7 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 48
4 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
Knowledge Check
If coefficient of static friction is μs and coefficient of kinetic friction is μk , which one is correct ?
Aμs=μkBμs>μkCμs<μkDμs≤μkA block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
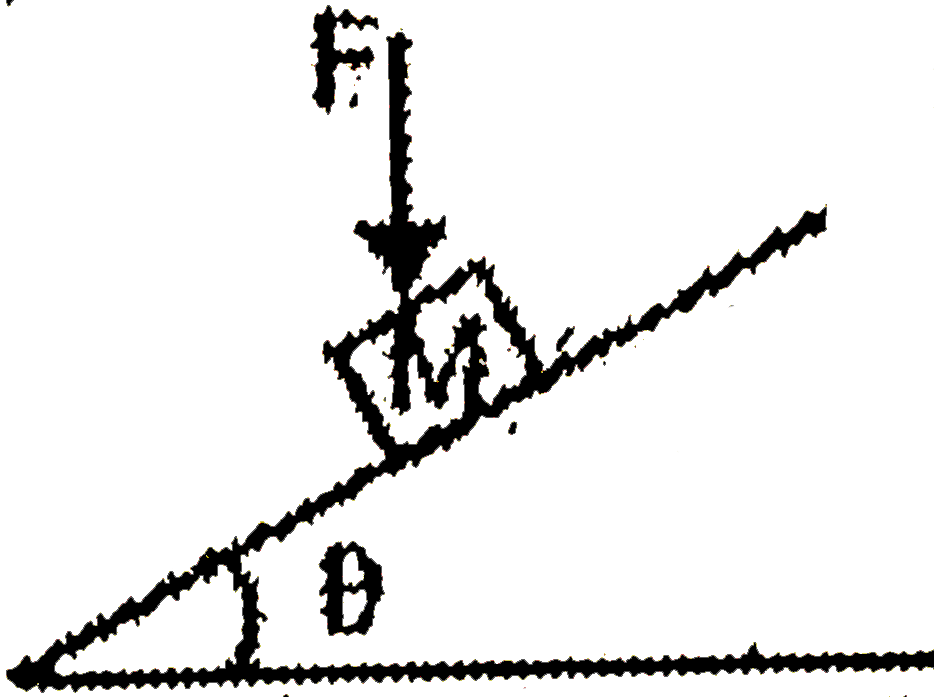 A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθ
A(F+Mg)sinθBμk(F+Mg)cosθCμsMgcosθD(Mg+F)sinθIf μk is the coefficient of kinetic friction, μl is the coefficient of rolling friction and us is the coefficient of static friction, then
Aμs>μk>μrBμs<μk<μrCμs<μr<μkDμsμr>μk
A block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionA wooden block of mass m resting on a rough horizontal table (coefficient of friction =μ ) is pulled by a force F as shown in figure.The acceleration of the block moving horizontally is:
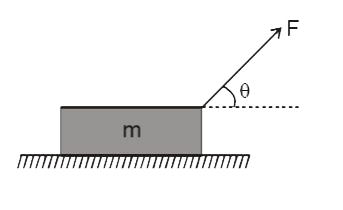
View SolutionA block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View SolutionA solid cylinder is rolling without slipping on a plane having inclination θ and the coefficient of static friction μs. The relation between θ and μs is
View Solution
