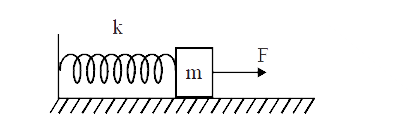
A block of mass m=2kg is connected to a spring of force constant k=50n/m. Initially the block is at rest and the spring has natural length . A constant force f=60N, is applied horizontally towards right, the maximum speed of the block (in m/s will be (neglect frication).

The correct Answer is:6
A block of ………………
For maximum speed,
dvdt=0⇒a=0
If at maximum speed, elongation is x, then
F=kx⇒x=Fk
Now, by WET,
−12kx2+Fx=12mv2
∴V=F√mk=6m/s
Similar Questions
A block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).
 View Solution
View SolutionInitially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
maximum extension in the springView Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
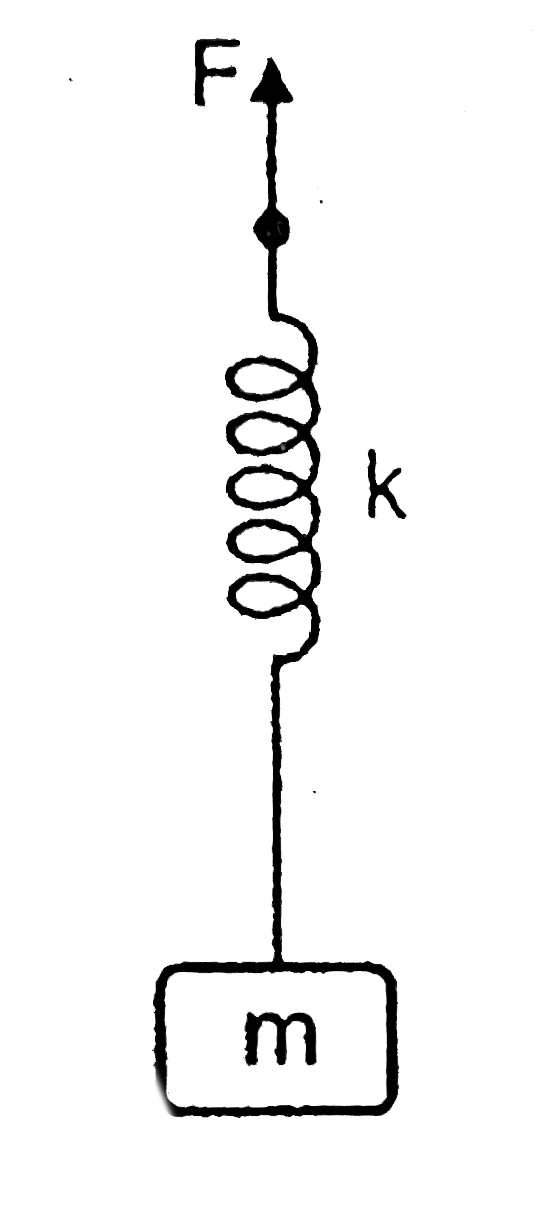 Amαk−gt−αt22Bmαk−gt−αt2Cmαk−gt+αt22Dmαk+gt+αt22
Amαk−gt−αt22Bmαk−gt−αt2Cmαk−gt+αt22Dmαk+gt+αt22 - Question 2 - Select One

A block of mass m initially at rest is dropped from a height h on to a spring of force constant k . the maximum compression in the spring is x thenAmgh=12kx2Bmg(h+x)=12kx2Cmgh=12k(x+h)2Dmg(h+x)=12k(x+h)2 - Question 3 - Select One
A block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
A(a) MF(m+M)B(b) mFMC(c) (M+m)FmD(d) mF(m+M)

Consider a block of mass 6 kg is attached to a spring having constant 16 Nm−1 . If the block is at rest initially and then stretched by a constant force of 20 N on frictionless surface as shown in figure . Caclculate the speed of the block when it has moved through a distance of 0.2 m from its initial position . dView SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction
 View Solution
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.
 View Solution
View Solution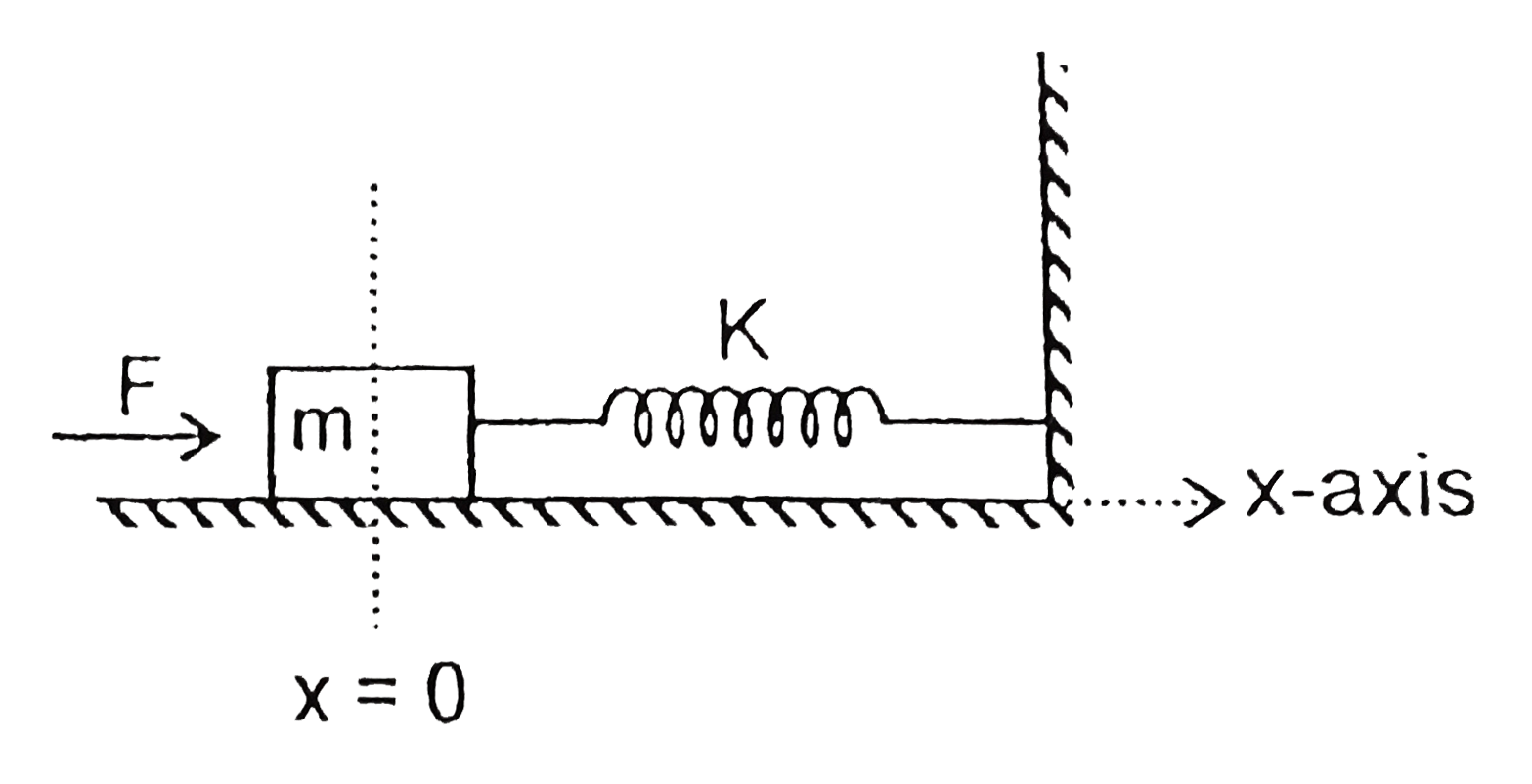
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ thenView SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View Solution

